
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доведення теорем евклідової геометрії в системі аксіом Г.Вейля.
Доведено такі теореми, що безпосередньо випливають з аксіом 1 - 5. Теорема 1: Будь-який з векторів простору Доведення: Дійсно для точок
Оскільки тору
Теорема 2: Доведення: Дійсно, припускаючи в аксіомі трикутника (5.2), що
Теорема 3: Якщо Доведення: Згідно з аксіомою трикутника 5.2 маємо: Далі за умовою нам треба згадати, що дано вектор і, отже, першою аксіомою 5.1 точки 10. Абсолютна геометрія. Абсолютна геометрія — частина класичної геометрії, незалежна від п'ятого постулату евклідової аксіоматики. Іншими словами, це спільна частина евклідової і неевклідової геометрії. Цей термін був запропонований угорським математиком Яношем Бойяї в 1832 р. Правда, сам Бойяї вкладав у нього дещо інший сенс: він називав абсолютною геометрією спеціально розроблену ним символіку, яка дозволяла об'єднувати однією формулою теореми як евклідової геометрії, так і геометрії Лобачевського. Перші 28 теорем «Начал» Евкліда належать до абсолютної геометрії. Приведемо декілька прикладів таких теорем: · У рівнобедрених трикутників кути при основі рівні. · При перетині двох прямих протилежні кути рівні. · Проти більшої сторони трикутника лежить більший кут, і навпаки, більшому куту протистоїть більша сторона. Оскільки п'ятий постулат визначає метричні властивості однорідного простору, відсутність його у абсолютній геометрії означає, що метрика простору не визначена, і більшість теорем, пов'язаних з вимірами (наприклад, теорема Піфагора) не можуть бути доведені у абсолютній геометрії. Перші 28 теорем «Почав» Евкліда відносяться до абсолютної геометрії. Прикладами інших теорем, недовідних в абсолютній геометрії, є численні еквіваленти V постулату.
Аксіоми вимірювання довжин відрізків. Теорія вимірювання є наслідком п'ятої групи аксіом Гільберта і п'ятої групи аксіом Вейля. Нехай маємо множину відрізків L i множину дійсних додатних чисел R+. Встановимо відображення L
Аксіома 1. Конгруентним відрізкам відповідають рівні числа. Аксіома 2. Якщо точка В лежить між точками A і C, тобто виконується порядок точок A
Аксіома 3. Завжди існує такий відрізок [KP], якому можна поставити у відповідність l одиницю. Означення. Число 1 називається мірою відрізка, а числа, які ставляться у відповідність довільним відрізкам називаються довжинами відрізків. В силу V-ї групи аксіом Вейля, маючи точку A, ми завжди можемо прикласти ненульовий вектор Нехай маємо два різних відрізки AB i CD, які конгруентні між собою: [AB] @ [CD]. Тоді, в евклідовому просторі завжди існує рух d, за допомогою якого відрізку [AB] можна поставити у відповідність відрізок [CD], конгруентний до [AB]. Але рух у евклідовому просторі породжується ортогональним перетворенням вектора векторного простору, який супроводжує відповідний евклідовий простір. Ортогональне перетворення векторів володіє властивістю збереження скалярного добутку двох векторів. Отже, якщо ми мали вектор
Розглядаючи відображення f, ми маємо право говорити, що відрізку [AB] ми поставили у відповідність довжину вектора Нехай маємо три точки A, B, C, для яких виконується порядок точок A
За аксіомою ІV.3 системи аксіом Вейля маємо, що
Якщо ми маємо
Аналогічно розглянемо |
| | За допомогою трьох точок A, B, C i відрізків [AB], [BC], [AC] ми можемо задати відображення f:
f([AB])=| f([BC])=| f([AC])=| Додамо рівності (1.1.3): f([AB])+f([BC])=t| Отже, аксіома А.2 виконується. Серед множини векторів можемо визначити такий вектор
12. Теорема про вимірювання довжин відрізків. Одиниці вимірювання довжин відрізків. Означення. Число 1 називається мірою відрізка, а числа, які ставляться у відповідність довільним відрізкам називаються довжинами відрізків.
Теорема 1.1.1. Відображення Доведення. І. Доведемо, що відображення 1. Нехай 2. Нехай маємо вектор | Покажемо, що коли норма вектора виражається числом, то f i
Тоді довжини співпадають: Отже, 3. Нехай маємо вектор 4. Нехай довжина вектора Нехай маємо ABk=ak, тоді оскільки ak < a, то точка Bk знаходиться між точками A i B (A | так, що виконується порядок точок A Задаючи відображення f: f([AB])=f([ABk])+f([BkB]), f([ABk])=| задамо відображення
Розглянемо три точки A, B, B'k, для яких має місце порядок точок
Розглянемо рівності (1.1.7) i (1.1.8). Якщо у нас існує числова функція
ak < Ми довели, що довжина вектора існує і є дійсним числом або може бути виражена дійсним числом. ІІ. Доведемо єдиність існування. Оскільки у нас завжди існує певний орт
Це означає, що відображення f єдине, а оскільки f і
Одиниці вимірювання довжин відрізків. Означення: довжиною відрізка називається невід’ємна скалярна величина, яка характеризує властивість лінійної протяжності та визначена для кожного відрізка так, що виконуються наступні аксіоми: 1. У множині S існує нульовий відрізок 0 такий, що m(0)=0 (символічно ця аксіома запишеться так: ([($0єS)(m(0)=0)]). 2. У множині S існує одиничний відрізок е такий, що m(е)=1, яким можна виміряти довжину будь-якого відрізка (символічно ця аксіома запишеться так: ([($еєS)(m(е)=1)]). 3. Рівні відрізки мають рівні довжини (символічно ця аксіома запишеться так: ([( " а,bєS)((a=b)↔ (mе(a)=mе(b))]). 4. Якщо відрізок а складається із скінченного числа відрізків b1, b2, b3,...bk, які прилягають один до одного кінцями, то довжина відрізка а дорівнює сумі довжин відрізків b1+b2+b3+...+bk (символічно: [( " а,b1,b2,b3,...bkєS)((a=b1+b2+b3+...+bk)↔ (mе(a)=mе(b1)+mе(b2)+mе(b3)+...+mе(bk))]). 5. (аксіома Архімеда) яким би великим не був відрізок а із множини S і яким би малим не був відрізок b із цієї ж множини завжди знайдеться натуральне число n таке, що відрізок а менший за відрізок n×b (символічно: [("а,bєS)($nєN)((а<n×b)↔ (mе(а)< n×mе(b))]). 6. (аксіома Кантора): нехай на довільній прямій МК дано нескінченну послідовність відрізків А1В1, А2В2, А3В3,...АnBn,... таку, що: 1) кожний наступний відрізок є частиною попереднього; 2) для будь-якого наперед заданого відрізка CD знайдеться натуральне число n таке, що АnВn<CD. Тоді на прямій МК існує єдина точка Р, що належить усім відрізкам послідовності. Аксіоми Архімеда та Кантора дають змогу повністю обґрунтувати теорію вимірювання довжин відрізків. На основі аксіоми Архімеда кожному відрізку аєS при вибраній одиниці довжини е можна поставити у відповідність певне невід’ємне дійсне число, яке є його довжиною. Відповідно до аксіоми Кантора можна зробити висновок про те, що і у випадку нескінченного процесу вимірювання, існує невід’ємне дійсне число, яке є його довжиною.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.179 (0.04 с.) |
 (
( Є
Є  ) є нульовим вектором
) є нульовим вектором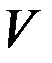 .
. є
є  =
= 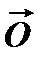 .
. = -
= -  .
. =
=  одержимо:
одержимо:  співпадають.
співпадають. =
=  .
. =
=  і за
і за R+, таке що кожному відрізку відповідало б певне дійсне додатне число, так щоб
R+, таке що кожному відрізку відповідало б певне дійсне додатне число, так щоб  задовольняло певним властивостям, які називаються метричними аксіомами.
задовольняло певним властивостям, які називаються метричними аксіомами. C, то:
C, то: ¹
¹  до точки A. Отримаємо
до точки A. Отримаємо  . В силу поняття рівності векторів, оскільки в нас встановлена норма вектора
. В силу поняття рівності векторів, оскільки в нас встановлена норма вектора  . За допомогою двох різних точок A і B ми завжди можемо визначити відрізок [AB] i, задавши відношення норми, ми певному відрізку можемо поставити у відповідність певне дійсне число, тобто f([AB])=|AB|. Доведемо, що f задовольняє трьом метричним аксіомам.
. За допомогою двох різних точок A і B ми завжди можемо визначити відрізок [AB] i, задавши відношення норми, ми певному відрізку можемо поставити у відповідність певне дійсне число, тобто f([AB])=|AB|. Доведемо, що f задовольняє трьом метричним аксіомам. , то в силу ортогонального перетворення j:
, то в силу ортогонального перетворення j: ,
,  2 =
2 =  2 =>
2 =>  |
|  |=|
|=|  |. (1.1.1)
|. (1.1.1) |, f([CD])=|
|, f([CD])=|  |. Але |
|. Але |  |=|
|=|  C. Отже, точки A, B, C лежать на одній прямій, =>
C. Отже, точки A, B, C лежать на одній прямій, => =t
=t  , 0<t<1. (1.1.2)
, 0<t<1. (1.1.2) +
+  =
=  =>
=>  =
=  -
-  ,
,  =
=  -t
-t  ,
, => 0<1-t<1.
=> 0<1-t<1. ,
, .
. |:
|: 2 =(1-t) 2
2 =(1-t) 2  2,
2, |2 =(1-t)2|
|2 =(1-t)2|  |2,
|2, |=(1-t)|
|=(1-t)|  |=t|
|=t|  |,
|, |=(1-t)|
|=(1-t)|  |.
|. |+(1-t)|
|+(1-t)|  |=f([AC]).
|=f([AC]). |=1. Але точки A i B визначають відрізок [AB], можна задати відображення f([AB])=|
|=1. Але точки A i B визначають відрізок [AB], можна задати відображення f([AB])=|  |=1. Отже, виконується аксіома А3.
|=1. Отже, виконується аксіома А3. вектор
вектор  =
=  |=1. Оскільки для відображення
|=1. Оскільки для відображення  . (1.1.4)
. (1.1.4) 1 =
1 =  =…=
=…=  =
= 
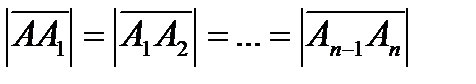 .
. n=n
n=n  , тоді
, тоді  . f([AAn])=|
. f([AAn])=|  n|=1,
n|=1,  . Тоді, |
. Тоді, |  B). Розглянемо вектор
B). Розглянемо вектор  '|= a'k, що a < a¢k, (1.1.5),
'|= a'k, що a < a¢k, (1.1.5), B'k. (1.1.6)
B'k. (1.1.6) :
: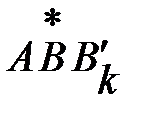 , тоді, в силу виконання метричної аксіоми А.2, отримаємо:
, тоді, в силу виконання метричної аксіоми А.2, отримаємо: =>
=>  .
.


