
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок построения теоретической кривой.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистический метод с применением закона Гаусса позволяет на основе выборки (например, N=20-50 штук и более) прогнозировать точность обработки всей обрабатываемой партии деталей. Графическая иллюстрация закона нормального распределения (закона Гаусса) представлено выше, а его математическое выражение характеризуется зависимостью
где Ф (x) - плотность вероятности x - переменная (случайная) величина;
e - основание натурального логарифма; Положение кривой относительно начала координат и ее форма определяются в основном двумя параметрами x и Среднее арифметическое
среднее-квадратичное отклонение
коэффициент вариации, характеризующий нестабильность исследуемого технологического процесса.
коэффициент относительной ассиметрии, характеризующий тенденцию к смещению центра группирования влево (
коэффициент эксцесса, характеризующий тенденцию кривой распределения к смещению вверх (
При анализе технологических процессов (ТП) или отдельных операций, указанные характеристики по данным выборки (Nв=20...50) принимают за истинные характеристики всей партии обрабатываемых заготовок или собираемых изделий (узлов). Если же одна из первичных погрешностей преобладает над остальными (удельный вес ее значительно больше остальных), тогда будет иметь место другой закон распределения случайных величин. Порядок расчета следующий. На основе выборки (Nв) из всей партии обрабатываемых заготовок (например, Nв = 20 шт. x1 = 8,02; 8,03;...; 8,14) определяется диапазон рассеивания (размах). R = Xmax - Xmin, R = 8,14 - 8,02 = 0,12 который разбивается на кассы (интервалы), а их число определяется по правилу Штюргерса K = 1 + 3,32 ln (Nв) ( принимается K= 6...10). Размер одного интервала C = R/K, C = 0,12/6 = 0,02. (19) В таблицу заносятся параметры интервалов, абсолютная частота (mi) появления контролируемого параметра в каждом из них и другие сведения. Таблица значений распределения
Данные таблицы представляются в виде гистограммы или фактического распределения, а затем определяются основные статистические характеристики нормального закона распределения.
Для построения теоретической кривой распределения необходимо выделить «точки перегиба: максимальную ординату
ординаты точек перегиба при X=+2 Y Y а также теоретическое поле рассеивания при y=0 X = Для приведения теоретической кривой к масштабу графика зависимости следует умножить на масштабный коффициент сNв, и затем и вычертить ее, совместив на одном графике фактическую кривую с теоретической. После построения графиков необходимо в масштабе нанести на них верхнюю (ES) и нижнюю (EJ) границы поля допуска, что позволяет визуально оценить возможный процент брака для всей исследуемой партии.
Далее необходимо выполнить проверку гипотезы о нормальности распределени я, например, вычислением среднего абсолютного отклонения (САО). САО = Xкрит. - где Xкрит - критическое (вызывающее сомнение) значение случайной величины Xi. В практических расчетах обычноограничиваются проверкой максимального и минимального значений из выборки. Условие нормального распределения
В этом случае, если условие нормальности не выполняется, следует исключить из выборки Xкрит. и вновь произвести расчеты всех статистических характеристик Если условие нормальности подтверждается, необходимо перейти к вычислению процента возможного брака, если нет - ограничиться построением гистограммы.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1062; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.115 (0.011 с.) |


 - среднеарифметическое отклонение (центр группирования);
- среднеарифметическое отклонение (центр группирования); - среднеквадратичное отклонение случайной величины xi от x;
- среднеквадратичное отклонение случайной величины xi от x; , которые являются первыми из пяти статистических характеристик.
, которые являются первыми из пяти статистических характеристик.


 ) или вправо (
) или вправо ( ),
),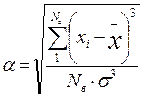
 ) или вниз (
) или вниз ( ) вдоль оси ординат
) вдоль оси ординат .
.

 0,4/
0,4/ 
 и X=-2
и X=-2 
 е
е 
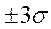

 /Nв,
/Nв, в
в ,
, 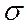 ,
,  ,
,  . Если и после второй проверки распределение не соответствует нормальному закону, необходимо дальнейшие расчеты прекратить.
. Если и после второй проверки распределение не соответствует нормальному закону, необходимо дальнейшие расчеты прекратить.


