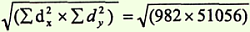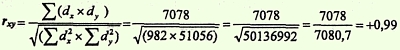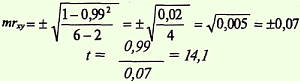ТЕМА 6. Измерение связи между явлениями. Методы изучения Корреляционных связей при оценке показателей здоровья и факторов окружающей среды

ЦЕЛЬ ЗАНЯТИЯ: Освоить принципы измерения корреляционной связи и овладеть методикой измерения связи между явлениями.

Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют коэффициенты корреляции по способу квадратов (Пирсона) и способу рангов (Спирмена); проводят оценки достоверности коэффициента корреляции. Оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Какие виды связи существуют между явлениями или признаками?

2. Является ли функциональная связь характерной для медико-биологических явлений?

3. Что такое корреляционная связь?

4. Можно ли считать, что при корреляционной связи значению одного признака соответствует несколько значений другого, взаимосвязанного с ним признака?

5. Можно ли утверждать, что корреляционная связь проявляется в массе наблюдений, т.е. в совокупности?

6. Что является критерием оценки характера и силы корреляции?

7. Можно ли утверждать, что коэффициент корреляции дает представление о наличии и направлении корреляционной связи?

8. С повышением температуры тела увеличивается частота пульса у большинства больных. Можно ли утверждать, что такая взаимосвязь относится к прямой корреляции?

9. Можно ли утверждать, что диапазон значений коэффициента корреляции находится в пределах от -1 до +1?

10. Каковы методы определения коэффициента корреляции?

11. Можно ли утверждать, что метод квадратов (Пирсона) дает более точные результаты по сравнению с методом рангов (Спирмена)?

12. Каков порядок определения коэффициента корреляции по методу рангов?

13. Как определяются характер и сила связи по коэффициенту корреляции?

14. Как оценивается достоверность коэффициента корреляции?

15. Можно ли утверждать, что если коэффициент корреляции более чем в три раза превышает свою ошибку, то он достоверен?

КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:

Задача каждой науки – вскрыть и изучить наиболее существенные связи между явлениями и процессами. Известны два вида связи между явлениями (признаками): функциональная и корреляционная. Функциональная связь отражает строгую зависимость процессов или явлений, и изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину. Функциональная связь, как правило, проявляется при физических и химических явлениях, где её можно представить в виде уравнения, формулы. Примером функциональной связи может являться увеличение объема шара в строгой зависимости от увеличения его радиуса, расширение тела по мере увеличения температуры нагревания и т.д. Корреляция – понятие, которое также означает взаимосвязь между признаками. При корреляционных связях, характерных для медико-биологических явлений, значению одного признака соответствуют разные значения других признаков. Корреляционная связь необходима, например, при оценке взаимосвязей между стажем работы и уровнем заболеваемости работающих; между разными уровнями физических факторов окружающей среды и состоянием здоровья; между различными уровнями интенсивности нагрузки и частотой (уровнем) физиологических реакций организма; между сроками госпитализации и частотой осложнений. Статистика позволяет исследователю измерить связи, обосновать выводы и наглядно их иллюстрировать. Корреляционная связь бывает положительной - прямой (при увеличении одного признака увеличивается другой) и отрицательной - обратной (при увеличении одного показателя другой уменьшается). Коэффициент корреляции свидетельствует не только о направлении связи, но и об уровне этой связи. Сильная связь выражается коэффициентом от 0,7 до 0,99, средняя — от 0,3 до 0,69, слабая — до 0,29. При нулевом значении коэффициента связи отсутствуют.

Наиболее простыми методом определения коэффициента корреляции являются ранговая корреляция: , где - коэффициент ранговой корреляции, d - разность рангов, n –число сопоставляемых пар признаков.При ранговой корреляции числовые выражения сравниваемых статистических рядов ранжируют, то есть проставляют ранговые номера для каждой цифры (от 1 и далее) и подставляют значения в формулу с учетом разницы порядковых значений.

Рассмотрим технику вычисления коэффициента ранговой корреляции на примере изучения связи между стажем работы (х) и числом травм (у):

 

 

Стаж работы в годах	Число травм	Порядковые номера (ранги)	Разность рангов	Квадрат разности рангов
X	Y	d(х-у)	d^2
До 1 года				-4
1-2				-2
3-4			2,5	+0,5	0,25
5-6			2,5	+1,5	2,25
7 и более				+4
	Σ d^2 = 38,5

Коэффициент ранговой корреляции составит:

Статистическая ошибка и критерий достоверности коэффициента корреляции вычисляются по формулам:

= 0.22, t = = 0,925/0,22= 4,2

Чтобы полученный коэффициент можно было считать достоверным, он должен превышать табличное значение (таблица значений критерия t по Н.А. Плохинскому ) при числе степеней свободы n - 1. В нашем случае величина критерия t (4,2) значительно выше критического значения критерия t (2.7) для уровня значимости р = 0.05 и числа степеней свободы = n −1=4. Зависимость между стажем работы и числом травм по приведенным данным достоверно прослеживается. Вывод: поскольку коэффициент корреляции ρ = -0,925, корреляционная связь обратная, сильная, вероятность безошибочного прогноза выше 95%, следовательно, мы можем утверждать, что с увеличением стажа работы число травм у рабочих уменьшается.

При расчете коэффициента корреляции методом квадратов (метод Пирсона) сначала вычисляют среднее значение в каждом вариационном ряду сравниваемых групп. Затем находят отклонение каждой величины ряда от полученной средней. Для устранения отрицательных значений эти величины возводят в квадрат и подставляют в формулу: r_{xy =} , где d_x и d_y – отклонение каждой варианты от своей средней арифметической М_х и М_y.По величине коэффициента устанавливают направление и силу связи. Достоверность коэффициента определяют по таблицам критических значений (таблицам Каминского) при числе степеней свободы n’ = n-2 (приложение, табл. 4), а также при расчете средней ошибки и критерия достоверности t. Коэффициент корреляции должен превышать свою ошибку не менее чем в 3 раза. Формула ошибки коэффициента ранговой корреляции: m = , t = По методу Пирсона ошибка коэффициента корреляции вычисляется по формуле: m_{r =} , t = . Значения t оценивается по таблице критических значений критерия t (при n<30, приложение, табл. 2).

Пример: определим направление и силу связи между количеством кальция в воде и жесткостью, если известны следующие данные

Жесткость воды (в градусах)	Количество кальция в воде (в мг/л)

Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант. Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).

 

 

Жесткость воды (в градусах)	Количество кальция в воде (в мг/л)	dх	dу	dх × dу	dx^2	dy^2
		-16 -12 -9 +7 +14 +16	-114 -86 -66 +48 +98 +120
Мх=Σ х / n	Му=Σ у / n		Σdх×dу=7078	Σdх^2=982	Σdy^2=51056
Мх=120/6=20	Мy=852/6=142

1. Определить средние величины M_x ряду вариант "х" и М_у в ряду вариант "у" по формулам: М_х = Σх/n (графа 1) и М_у = Σу/n (графа 2).

2. Найти отклонение (d_х и d_у) каждой варианты от величины вычисленной средней в ряду "x" и в ряду "у" d_х = V — М_х (графа 3) и d_y = V — М_у (графа 4).

3. Найти произведение отклонений d_x х d_y и суммировать их: Σ d_х х d_у (графа 5).

4. Каждое отклонение d_x и d_у возвести в квадрат и суммировать их значения по ряду "х" и по ряду "у": Σ d_x² = 982 (графа 6) и Σ d_y² = 51056 (графа 7).

5. Определить произведение Σ d_x² х Σ d_y² и из этого произведения извлечь квадратный корень.

6. Полученные величины Σ (d_x x d_y) и √(Σd_x² x Σd_y²) подставляем в формулу расчета коэффициента корреляции:

7. Определить достоверность коэффициента корреляции:

1-й способ. Найти ошибку коэффициента корреляции (mr_xy) и критерий t по формулам:

Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.

2-й способ оценки достоверности коэффициента корреляции. Достоверность коэффициента корреляции оценивается по таблице "Стандартные коэффициенты корреляции,считающиеся достоверными (по Л.С. Каминскому) " (приложение, табл. 4). При числе степеней свободы (n — 2) = 6 – 2 = 4 наш расчетный коэффициент корреляции r_xу = + 0,99 больше табличного (r_табл = + 0,917 при р = 99%).

Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: r_ху = + 0,99, р > 99,9%).

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:

ЗАДАНИЕ 1: Вычислить коэффициент ранговой корреляции, определить направление и силу корреляционной связи, оценить достоверность полученных данных

Задача 1

Существует ли связь между стажем работы на машиностроительном предприятии и показателями заболеваемости рабочих?

Стаж работы	До 1 года	1-3 года	4-5 лет	6-10 лет	11-15 лет	16-20 лет	21-25 лет	26 и более
Число случаев заболеваний на 100 рабочих	59,6	41,9	40,8	64,7	64,7	77,5	83,6	112,8

Задача 2

Существует ли связь между возрастом заболевших гриппом и уровнем смертности от этого заболевания?

Возраст заболевших в годах	До 1 года	1-4	5-9	10-14	15-17	18-20	21-30	31-40	41-50	51-60	61 и старше
Смертность на 100000 человек	68,3	57,7	55,9	24,7	55,9	42,1	67,9	86,6	89,4	106,7	158,2

Задача 3

Существует ли связь между возрастом мужчин и уровнем смертности?

Возраст в годах	0-4	5-9	10-14	15-24	25-34	35-44	45-54	55-64	65 и старше
Уровень смертности на 100000 человек	801,0	272,0	194,7	296,8	624,1	922,8	2624,4	4324,5	9275,1

Задача 4

Существует ли связь между долей контингента часто болеющих (ЧБ) и возрастом детей?

Возраст в годах	До 1 года	1-2	3-4	5-6	7-8	9-10	11-12	13-14
Доля ЧБ	28,5	48,2	44,9	38,7	38,7	27,9	24,2	20,1

Задача 5

Существует ли связь между возрастом и частотой нарушения зрения у детей?

Возраст в годах	0-3	4-5	6-7	8-9	10-11	12-13	14-15	16-17
Нарушения зрения, ‰	18,9	20,7	31,4	42,7	42,1	54,6	54,6	92,0

Задача 6

Существует ли связь между порядковым номером месяца года и частотой обращения населения за скорой и неотложной медицинской помощью по поводу сердечно-сосудистых заболеваний?

Месяц	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
Частота обращений за СНМП ‰	114,3	108,3	109,7	103,2	104,5	95,2	98,4	97,8	87,6	92,7	92,7	96,4

Задача 7

Существует ли связь между расстоянием от места жительства до предприятия и заболеваемостью рабочих?

Расстояние в метрах	До 500 м	600-1000	1100-3000	3100-4000	4100-5000	5100-7000	7100-9000	9100 и более
Заболеваемость ‰	920,1	887,9	920,1	954,0	1286,3	1107,8	1510,8	1832,7

Задача 8

Существует ли связь между временем прошедшим от возникновения острого приступа холецистита до начала проведения операции и частотой послеоперационных осложнений?

Время в часах	До 3 часов	3-5	6-8	9-11	12-14	15-17	18-20	21-23	24 и более
Частота осложнений в %

Задача 9

Существует ли связь между возрастной группой и частотой самоубийств у мужчин?

Возрастная группа умерших, годы	До 20	20-29	30-39	40-49	50-59	60-69	70 и старше
Частота самоубийств на 100 тыс. чел.	4,1	28,5	43,8	54,8	54,8	48,2	75,5

Задача 10

Существует ли связь между возрастной группой мужчин и распространенностью психических заболеваний?

Возрастная группа, годы	0-4	5-9	10-14	15-19	20-24	25-29	30-39	40-49	50-59	60-69	70 и старше
Заболеваемость ‰	16,2	35,4	31,2	8,1	10,2	35,0	31,4	53,1	58,8	30,5	19,2

Задача 11

Существует ли связь между возрастом ребенка и количеством больных с эквиноварусной деформацией стоп, обусловленной спастическими парезами в нижних конечностях?

Возраст	До 1 месяца	1- 3 месяца	4 – 6 месяцев	7-9 мес.	10-12 мес.	1-2 года	2-3 года	Старше 3 лет
Кол-во больных

Задача 12

Существует ли связь между возрастной группой и уровнем травматизма у мужчин?

Возрастная группа мужчин, годы	Дети от 0 до 14 лет	15-17	18-19	20-29	30-39	40-49	50-59	60-69	70 и старше
Частота травматизма на 100 тыс. чел.	72,3	165,6	233,6	196,9	157,2	176,3	153,3	141,9	97,2

Задача 13

Существует ли связь между возрастом и уровнем смертности женщин в Российской Федерации?

Возраст в годах	До 1 года	1-4	5-9	10-14	15-24	25-34	35-44	45-54	55-64	65 и старше
Уровень смертности на 100000 человек	10,9	0,7	0,3	0,3	0,85	1,8	3,6	7,7	15,4	113,9

Задача 14

Существует ли связь между возрастной группой пациентов и долей полностью удовлетворенных качеством лечения в стационаре?

Возраст в годах	15-20	21-25	26-30	31-35	36-40	41-45	46-50	51-55	56-60	61 и и старше
% удовлетворенных качеством лечения	77,6	81,1	75,2	64,3	64,3	50,1	48,9	46,2	39,9	20,7

 

ЗАДАНИЕ 2: Вычислить коэффициент корреляции методом квадратов (Пирсона), определить направление и силу корреляционной связи, оценить достоверность полученных данных.

Задача 1

Существует ли связь между долей детей, охваченных прививками против кори, и уровнем заболеваемости корью?

Охвачено прививками, %
Заболеваемость на 100 тыс. чел.

Задача 2

Существует ли связь между ростом и массой тела у студентов-медиков в возрасте до 19 лет?

Рост в см.
Масса, кг

Задача 3

Существует ли связь между стажем работы в цехах с вредными условиями труда и кратностью заболеваемости с временной утратой трудоспособности?

Стаж работы (лет)
Кратность случаев ВН (раз)

Задача 4

Существует ли связь между длиной и массой тела у новорожденных?

Длина, см
Масса, кг	2,4	3,1	4,1	3,6	3,2	3,3	3,5	3,8	3,5	3,8	4,0

Задача 5

Существует ли связь между количеством бактерий, вырастающих при посеве 0,1 мл обеззараженной воды, и дозой остаточного хлора в 1 мл воды?

Доза остаточного хлора (мг/л)	0,05	0,10	0,07	0,60	2,00	1,00	0,80	1,2	3,00
Число бактерий

Задача 6

Существует ли связь между возрастом родильницы и количеством грудного молока?

Возраст в годах
Лактация в гр

Задача 7

Существует ли связь междудлительностью охлаждения организма и уровнем молочной кислоты (мг%)?

Дни охлаждения
Уровень молочной кислоты мг%	7,0	7,0	7,2	7,1	8,5	8,9	8,7	8,9	9,0	9,5

Задача 8

Существует ли связь между возрастом пациентов и потребностью их в медицинской помощи (эквивалентные единицы на 1 чел.)?

Возраст в годах
Потребность в мед. помощи	10,0	7,0	2,2	2,0	2,0	3,5	5,0	7,5	10,1	12,0

Задача 9.

Существует ли связь между температурой воздуха осенью и частотой возникновения ОРВИ?

t воздуха
Случаи ОРВИ

Задача 10.

Существует ли связь между возрастом и заболеваемостью студентов медицинского университета?

Возраст, лет
Заболеваемость на 1000 чел.

Рекомендуемая литература.

· Медик В.А., Юрьев В.К. Общественное здоровье и здравоохранение. Учебник для вузов: - М: ГЭОТАР – Медиа. - 2012, - 608 с.

· Медик В.А. Общественное здоровье и здравоохранение: Руководство к практическим занятиям: - М: ГЭОТАР – Медиа. - 2012, - 400 с.

· Щепин О.П., Медик В.А. Общественное здоровье и здравоохранение. Учебник для вузов: - М., 2011, - 592 с.

· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.

· В.К. Юрьев, Г.И. Куценко. Общественное здоровье и здравоохранение. С.-П., 2000. –с.199-201.

· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002. –с. 110-112.

 

 

ТЕМА 7. Динамические ряды

ЦЕЛЬ ЗАНЯТИЯ: Овладеть методикой составления и обработки динамических рядов.

Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно преобразуют динамические ряды с целью выявления особенностей изучаемого процесса и достижения наглядности в характеристике того или иного явления, графически изображают полученные данные для определения тенденции изучаемого явления, рассчитывают показатели динамического ряда. Оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. В каких случаях обработки и анализа статистического материала прибегают к составлению динамических рядов? Что представляет собой динамический ряд?

2. Что такое уровни динамического ряда?

3. Какой динамический ряд называется простым и какой производным?

4. Что такое моментный динамический ряд?

5. Перечислите основные приемы выравнивания динамического ряда. Назовите составляющие анализа динамического ряда.

6. Какие показатели рассчитывают для анализа динамического ряда?

7. Почему для анализа динамического ряда его изображают графически?

КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:

В практическом здравоохранении или проведении медико-социальных исследований и в клинических работах часто требуется выявить основную закономерность изучаемого явления. В таких случаях, как правило, составляют динамический ряд. Динамический ряд — это ряд однородных статистических величин, показывающих изменение явления во времени. Динамический ряд может быть представлен абсолютными числами (изменение числа больных), средними величинами (среднее число лабораторных анализов за неделю) и относительными показателями (изменение рождаемости, заболеваемости, травматизма, обеспеченности врачами). Числа, из которых состоит динамический ряд, называются уровнями ряда. Если колебания уровней значительные, и выявить закономерность затруднительно, динамический ряд выравнивают. Существуют различные методы выравнивания динамического ряда: укрупнение интервалов, расчет скользящей средней и другие, позволяющие устранить влияние случайных колебаний на уровни динамического ряда.

Укрупнение интервала производят путем суммирования данных за ряд смежных периодов. Как видно из табл.5, помесячные числа заболеваний ангиной то увеличиваются, то уменьшаются. После укрупнения интервалов по кварталам года можно увидеть определенную закономерность, наибольшее число заболеваний приходится на летне-осенний период.

Таблица 5

Сезонные колебания случаев ангины в городе А. в 2014 г.

Месяц	I	II	III	IV	V	VI
Число заболеваний по месяцам
по кварталам

 

VII	VIII	IX	X	XI	XII	Итого за2014 г.

Вычисление групповой средней для каждого укрупненного периода производят так: суммируют смежные уровни соседних периодов, а затем полученную сумму делят на число слагаемых (табл. 6).

Таблица 6

Динамика процента расхождений клинических и патологоанатомических диагнозов по данным больницы города А.

Годы
Процент расхож- дения диагнозов	11,0	9,8	8.0	9,2	8,2	8,6	8,5	7,9
Групповая средняя	10,4	8,6	8,4	8,2

Для уровней динамического ряда, представленных в табл. 6, характерны волнообразные колебания. Выравнивание ряда путем вычисления групповой средней позволило получить данные, иллюстрирующие довольно четкую тенденцию к постепенному снижению процента расхождений диагнозов в больнице.

Вычисление скользящей средней позволяет каждый уровень заменить на среднюю величину из данного уровня и двух соседних с ним (табл. 7).

Ряд, выровненный при помощи скользящей средней, представляет последовательную тенденцию снижения процента расхождения диагнозов. Таким образом, скользящая средняя является простейшим способом выравнивания ряда. Этот метод дает возможность сгладить, устранить резкие колебания динамического ряда.

Таблица 7

Методика расчета скользящей средней

Годы
Процент расхож- дения диагнозов	11,0	9,8	8.0	9,2	8,2	8,6	8,5	7,9
Скользящая средняя	-	9,6	9,0	8,7	8,6	8,4	8,3	-

Ряд, выровненный с помощью скользящей средней, иллюстрирует общую четкую тенденцию: постепенное уменьшение показателей частоты расхождения диагнозов.

Анализ динамического (временного) ряда сводится к вычислению следующих показателей: абсолютного прироста (или снижения); темпа роста (или снижения); темпа прироста; значения 1% прироста, показателей наглядности. Абсолютный прирост представляет собой разность между последующим и предыдущим уровнем. Темп роста — это отношение последующего уровня к предыдущему, умноженное на 100%. Темп прироста является отношением абсолютного прироста (снижения) к предыдущему уровню, умноженным на 100%. Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста. Показатель наглядности показывает отношение каждого уровня ряда к одному из них (чаще начальному), принятому за 100%.

1) Абсолютный прирост или убыль (абсолютный размер разности уровней) - разность между последующим и предыдущим уровнями (дает возможность анализировать скорость происходящих изменений в ее абсолютном выражении).

2) Темп прироста или убывания - процентное отношение абсолютного прироста (или снижения) к предыдущему уровню.

3) Темп роста или снижения - процентное отношение последующего уровня к предыдущему.

4) Для анализа динамического ряда используются также показатели наглядности, хотя следует помнить, что для коэффициента наглядности не обязательны взаимосвязанные динамические изменения.

Динамические ряды характеризуют изменение показателей здоровья - уровень и темп снижения заболеваемости, демографические сдвиги (рождаемости, общей и младенческой смертности), изменения физического развития. Пример анализа динамического ряда (табл. 8).

Таблица 8

Динамика рождаемости в сельском поселении за 2010 - 2014 гг.

Год	Число родившихся на 1000 населения	Абсолютный прирост	Темп прироста	Темп роста	Показатель наглядности
	8,7 8,9 8,8 8,5 8,3	- 0,2 -0,1 -0,3 -0,2	- 2,6% -1,3% -3,8% -2,7%	- 102,6% 98,7% 96,2% 97,3%	100,0% 102,6% 101,3% 97,4% 94,8%

Расчет показателей динамического ряда:

1) Абсолютный прирост: 8,9 - 8,7 = 0,2

8,8 - 8,9 = - 0,1 и т.д.

2) Темп прироста: 0,2: 8,7 × 100% = 2,3%

-0,1: 8,9 × 100% = - 1,1% и т.д.

3) Темп роста: 8,9: 8,7 × 100% = 102,3%

8,8: 8,9 × 100% = 98,87% и т.д.

4) Показатель наглядности: уровень 2010 г. принимаем за 100%

8,9: 8,7 × · 100% = 102,3%

8,8: 8,7 × 100% = 101,1% и т.д.

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ: