
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация экспериментальных схемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Настало время просмотреть все экспериментальные схемы, приведенные в нашей книге. В последней главе новых схем не прибавится: там пойдет речь о корреляционных исследованиях, а в них экспериментатор уже не изменяет своих независимых переменных самостоятельно. Обсуждавшиеся нами эксперименты отличаются друг от друга по трем основным параметрам. Соответствующие им различения были введены в четвертой, седьмой и настоящей главах.
В самых первых экспериментах, где участвовал только один испытуемый, внутренняя валидность обеспечивалась за счет различного упорядочивания проб: использовались их регулярное чередование, случайная или позиционно уравненная последовательности. Даже если увеличить число испытуемых в подобных экспериментах, контроль внутренней валидности останется прежним. Иначе говоря, сравнение условий, или уровней, независимой переменной проводится здесь интранидивидуально. Если же внутренняя валидность эксперимента обеспечивалась с помощью привлечения разных групп испытуемых для каждого из условий, или уровней, независимой переменной, то сравнение результатов действия последних проводилось по межгрупповой схеме. А в экспериментах предыдущей главы для обеспечения внутренней валидности каждому испытуемому предъявлялась определенная позиционно уравненная последовательность уровней независимой переменной. В результате сравнение между уровнями проводилось кросс-индивидуально. Таким образом, первый параметр; классификации экспериментальных схем можно назвать способом сравнения условий, или уровней, независимой переменной: интраиндивидуальное, межгрупповое или кросс-индивидуальное.
В предыдущей главе было введено еще одно различение. Если в одних экспериментах используется два (или несколько) качественно разных условия, или уровня, независимой переменной, то в других экспериментах они могут быть выражены количественно. Мы обсуждали это совсем недавно, и вам должно быть понятно, о чем идет речь. Второй основной параметр экспериментальных схем — это тип изменения независимой переменной: качественный или количественный.
Третье различение экспериментальных схем введено в настоящей главе. В экспериментах используются либо одна, либо несколько независимых переменных. Число независимых переменных и есть третий основной параметр: либо эксперимент с одной переменной, либо факторный эксперимент.
Поскольку у нас есть три основания сравнения условий, два типа независимых переменных и два варианта по их числу, то, по всей видимости, мы должны получить ровно 12 различных ячеек для размещения любых экспериментальных схем. Некоторые эксперименты, описанные в нашей книге, действительно, можно распределить по этим ячейкам. Примеры приведены в табл. 8.2. Скажем, в эксперименте Дененберга и Мортона (1962) с прошлым опытом для каждой из независимых переменных — содержания детенышей во время и после вскармливания — использовалось межгрупповое сравнение, причем обе эти переменные изменялись качественно. Этот эксперимент точно попадает в ячейку № 8. Однако не всякий факторный эксперимент можно столь же успешно занести в одну из приведенных ячеек. Ведь используемые независимые переменные (две или несколько) могут различаться по способам сравнения условий или по типу их изменения. Поэтому возможных сочетаний введенных нами параметров гораздо больше 12. (В эксперименте Гаффана, где обезьяны решали задачи на выбор по образцу с различной временной отсрочкой, сравнение условий одной независимой переменной — состояния свода — было, естественно, межгрупповым, а сравнение уровней другой независимой переменной — интервала отсрочки — проводилось кросс-индивидуально. Кроме того, состояние свода изменялось качественно (т. е. либо рассечен, либо нет), а интервал отсрочки — количественно (три уровня).
Если обе независимые переменные одинаковы и по способу сравнения условий, и по типу изменения, как в эксперименте Дененберга и Мортона, то схема называется гомогенной. А если они различаются по этим параметрам, как в эксперименте Гаффана, то схема становится гетерогенной. Факторные эксперименты часто классифицируют по числу уровней каждой независимой переменной. В исследовании Дененберга и Мортона (1962) использовалась схема «2X2», а Гаффан (1974) в своем эксперименте с разными отсрочками использовал схему «2X3».
Изложенная трехмерная классификация экспериментальных схем основывается на главных параметрах. Как вы помните, в индивидуальных экспериментах не используются различные последовательности предъявления проб, в экспериментах с межгрупповым сравнением — разные способы построения групп: случайное распределение, случайный отбор из предварительно выделенных «слоев» и т. д. Поэтому, прочитав целую подписку психологического журнала, вы можете не обнаружить даже двух одинаковых экспериментов, полностью подобных по своим схемам.
Таблица 8.2. 12 гомогенных экспериментальных схем
КРАТКОЕ ИЗЛОЖЕНИЕ
Для проверки гипотезы о воздействии рассечения свода у обезьяны на ее способность узнавания нужно было провести два факторных эксперимента: один — чтобы определить, нарушается ли при этом именно память, а другой — чтобы установить специфичность се нарушения. В каждом из этих экспериментов помимо первичной изучаемой переменной — состояния свода — привлекалась вторая независимая переменная, факторным называется эксперимент с использованием по крайней мере двух независимых переменных.
В итоге факторного эксперимента определяются основной результат действия каждой из независимых переменных и взаимодействие между ними. На примере эксперимента с рассеченным сводом мы раскрыли конкретное содержание основных результатов и взаимодействия и показали способы их измерения (когда две независимые переменные имеют по два уровня). Основной результат действия независимой переменной — это разность между общими средними значениями зависимой переменной по каждому из уровней. Взаимодействие — это разность между двумя разностями по каждому из уровней второй независимой переменной.
Основные вилы взаимодействия, которые можно получить в факторных экспериментах, иллюстрировались графически. Здесь же представлены и способы измерения основных результатов и взаимодействий. Одна из независимых переменных помещается на горизонтальной оси, и затем по соответствующим значениям зависимой переменной строятся отдельные графики для каждого из уровней другой независимой переменной. Если отрезки, полученные таким образом для второй независимой переменной, параллельны, взаимодействие отсутствует (т. е. нулевое). Если отрезки расходятся вправо или влево, взаимодействие называют расходящимся. А если они пересекают друг друга, то это пересекающееся взаимодействие.
Факторные эксперименты часто применяются для проверки гипотез с одним отношением, т. е. для определения результата влияния одной независимой переменной на поведение. Именно такие гипотезы обсуждались нами в предыдущих главах. Центральная задача в таких экспериментах — устранить сопутствующее смешение, как естественное, так и искусственное. Если, согласно гипотезе, независимая переменная действует на определенную базисную переменную, то с помощью факторного эксперимента можно обеспечить контроль за выделением этого воздействия. Однако при том условии, которое организуется для определения воздействий различных уровней изучаемой независимой переменной, последняя может по-разному влиять и на вторую базисную переменную. Это показано на примерах экспериментов Гаффана (1974) с рассечением свода у обезьян. Чтобы устранить смешение собственно памяти с восприятием, между пробой-образцом и пробой-выбором давались не только длинные, но и короткие интервалы отсрочки. При коротком интервале для правильного выбора не нужно запоминать предмет надолго. Смешение способности к узнаванию и запоминания по ассоциации устранялось путем использования чисто ассоциативных задач, для решения которых не нужно опознавать предъявляемые предметы. В каждом из этих экспериментов второй уровень контрольной переменной не оказывал никакого воздействия на предполагаемую базисную переменную. Показателем успешности разделения предполагаемой и сопутствующей переменных служил факт расходящегося взаимодействия между ними. Таким образом, применение факторной схемы позволило получить результаты, близкие к результатам идеального (чистого) эксперимента, в котором можно было бы исследовать только базисную переменную. Тем самым повышается внутренняя валидность эксперимента. Использование факторных схем позволяет повысить и внешнюю валидность. Прежде всего в тех случаях, когда нужно проверить гипотезу о непосредственном простом действии независимой переменной. Согласно альтернативной гипотезе, воздействие является комбинированным, т. е. активный уровень независимой переменной дает результат только благодаря сочетанию с активным уровнем дополнительной переменной. Так, Вайз и Даусон (1974), проводя опыты на крысах, предполагали, что лекарственный препарат диазепам непосредственно приводит к увеличению количества съедаемой пищи, повышая аппетит. Согласно же комбинированной гипотезе, лекарство действует не прямо, а снимая состояние тревожности. В опытах, проводившихся как в новой обстановке, вызывающей у крыс подобное состояние, так и в домашних клетках, было обнаружено значительное различие в количестве съеденной пищи между животными с инъекцией диазепама и с инъекцией плацебо. Тем самым удалось показать, что действие диазепама является непосредственным, оно не зависит от уровня тревожности. А если бы результат действия зависел от уровня дополнительной переменной, то обобщать его было бы нельзя. При проверке обобщения результатов следует учитывать не только факторы, вызванные участием экспериментатора, но и индивидуальные различия испытуемых. Для того и привлекались девочки-индианки в экспериментах по изучению трудовой этики, чтобы распространить полученные результаты на людей, принадлежащих к разным культурным группам. При использовании схем позиционного уравнивания эксперимент автоматически становится факторным. Помимо изучаемой независимой переменной здесь появляется переменная местоположения каждой пробы в порядке их предъявления. В кросс-индивидуальном эксперименте с позиционным уравниванием определяется среднее значение по данным всех испытуемых для первой пробы, затем для второй и т. д. Однако главное преимущество факторных экспериментов — это возможность проверять настоящие комбинированные гипотезы. Например, для проверки гипотезы, известной теперь как закон Йеркса — Додсона, оптимальная сила напряжения, способствующего хорошему изучению, должна понижаться с увеличением трудности задач — нужно было использовать задачи различных уровней трудности различения. Далее обсуждаются факторные эксперименты, в каждом из которых был получен одни из основных видов взаимодействия, описанных нами выше. Нулевое взаимодействие было установлено в эксперименте Стернберга (1969) с изменением четкости опознаваемою тестового стимула и размера ранее предъявленного набора знаков. В эксперименте Дененберга и Мортона (1962) с использованием двух независимых переменных — условий содержания крыс во время и после вскармливания — было обнаружено расходящееся взаимодействие. А пересекающееся взаимодействие было получено в эксперименте по изучению времени реакции, проведенном Саймоном и Руделлом (1907). Одной независимой переменной был тип команды («левая» и «правая»), а другой — ухо, на которое она подавалась (левое и правое). Выяснилось, что значительное влияние на время реакции оказывает то, с кокой стороны поступает сигнал (а эта переменная была нерелевантной). В тех случаях, когда «ухо» не совпадало с типом команды, время реакции возрастало. В каждом из упомянутых экспериментов для проверки комбинированных гипотез нужно было использовать факторную схему. Оценить справедливость соответствующих теорий и моделей, привлекая только одну независимую переменную, было бы невозможно. Взаимодействие, полученное Йерксом и Додсоном, подтвердило теорию о двух базисных переменных — различения стимулов и ассоциирования, на каждую из которых сила электроудара оказывала противоположное воздействие. Результаты Дененберга и Мортона можно объяснить тем, что приручение в период вскармливания делает крыс неспособными к использованию всех преимуществ свободного передвижения для дальнейшего успешного научения в лабиринте. Результаты, полученные Стернбергом, подтвердили предложенную им модель разделения стадий процесса обработки информации — кодирование стимула и сканирование ранее предъявленного набора знаков при опознании одного из них. А обнаруженная Саймоном и Руделлом прочная связь между стимулируемым ухом и типом команды остается пока интригующей загадкой.
Существуют эксперименты, где изучаемых независимых переменных — больше двух, в них проверяются более сложные комбинированные гипотезы. Взаимодействие между двумя переменными называется взаимодействием первом порядка, между тремя — взаимодействием второго порядка и т. д.
Все обсуждавшиеся нами экспериментальные схемы можно классифицировать по трем основным параметрам. Первый параметр —это способ сравнения условий, или уровней, независимой переменной: сравнение по каждому испытуемому, межгрупповое сравнение или сравнение по всем испытуемым. Второй — это характер изменения независимой переменной: качественный или количественный. И третий — число независимых переменных: либо эксперимент с одной переменной, либо факторный эксперимент. Схемы не обязательно должны быть одинаковы (гомогенны) в отношении каждой из независимых переменных. Например, для одной независимой переменной может применяться межгрупповое сравнение, а для другой – интраили кросс-индивидуальное.
ВОПРОСЫ 1. С какой целью в эксперименте с рассечением свода использовалось несколько временных интервалов между пробой-образцом и пробой-выбором? 2. Приведите примеры основных результатов и взаимодействия в факторных экспериментах. 3. Как измеряются основные результаты действия независимых переменных на графике? 4. Опишите, как вырядят на графиках основные виды взаимодействия двух независимых переменных (если у каждой из них – по два уровня). 5. Почему в экспериментах по проверке гипотез о воздействии независимой переменной на определенную базовую переменную часто требуется контрольная переменная? 6. Расскажите, как использовать несколько уровней второй независимой переменной для повышения внешней валидности. 7. Почему для проверки закона Йеркса — Додсона был необходим факторный эксперимент? 8. Каким образом вытекает конкретная комбинирования гипотеза, проверенная в эксперименте Стернберга, из предложенной им модели процесса обработки информации? 9. Изобразите на графике такие экспериментальные результаты, которые могли бы быть получены, если бы приручение крыс в период вскармливания не влияло на успешность их научения в лабиринте, а содержание в просторных ящиках после вскармливания оказывало большую помощь, чем содержанке в тесных клетках. 10. Придумайте комбинированную гипотезу, которая подтверждалась бы наличием пересекающегося взаимодействия. (Постарайтесь отвлечься от исследования Саймона и Руделла.) 11. Какое место (и почему) занимает эксперимент Иеркса и Додсона в системе экспериментальных схем?
СТАТИСТИЧЕСКОЕ ПРИЛОЖЕНИЕ: ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Для того чтобы при наличии двух независимых переменных проверить статистическую значимость двух результатов действия независимой переменной, а также взаимодействие между переменными, применяется F-критерий. Принципы его применения точно такие же, как и описанные в предыдущем приложении. Для того чтобы выявить, достаточно ли величина отношения превышает 1, чтобы отвергнуть нуль-гипотезу, производится сравнение межгрупповой оценки дисперсии генеральной совокупности с внутригрупповой оценкой.
Как получить внутригрупповую оценку, уже было показано. Межгрупповая оценка определяется раздельно для каждого из двух основных результатов действия и для взаимодействия. Таким образом, вычисляются три величины F; каждая полученная величина сравнивается с табличным значением критерия для альфа-уровня, равного 0,05 или 0,01. Это значение критерия можно найти в статистической таблице 3.
Эксперимент с двумя независимыми переменными
Давайте по-другому рассмотрим четыре выборки наших данных по времени реакции. Допустим, что на самом деле эксперимент на время реакции проводился с двумя независимыми переменными: одной из них был тип стимула – свет или тон, другой – тип реакции: простая реакция или реакция выбора. Простая реакция означает нажатие левой кнопки, когда сигнал появляется слева, нажатие правой – когда он появляется справа. Вернемся к исходным обозначениям: условие А представляет простую реакцию на световой стимул; условие Б – простую реакцию на тон; условие В – реакцию выбора на свет; Τ – реакцию выбора на тон. Опыт проводился на четырех группах по 17 испытуемых. Ниже приводятся средние времена реакций, полученные для четырех групп испытуемых.
Различие, связанное с ответом (типом реакции), представлено в этом случае различием между строками, а различия, – вызванные стимулом, представлены различиями между столбцами. Таким образом, произведение реакции на стимул есть произведение строки на столбец (стр×стл). В матрице г строк и с столбцов, в нашем случае r=с=2. Внутригрупповое среднее квадратичное
Для тех же четырех групп данных можно использовать предыдущие расчеты для вычисления среднего квадратичного внутри группы (СКВВГ):
Или
СКВГ = 4306 + 5808 + 5391 + 4673 = 20178.
Как вы заметили, индексы у слагаемых уже новые. ∑х2r1c1 означает, что (полученная внутри группы величина х2 соответствует строке 1 (простая) и столбцу 1 (тон). Точно так же ∑х2r2c2 означает величину для строки 2 (выбор) и столбца 2 (свет) и т. д.
Здесь для нахождения среднего квадратичного можно снова применить формулу (7.6) (поскольку r×с = k):
Из того, что 68 испытуемых делятся на 4 группы, как и ранее, следует
Среднее квадратичное по строкам
Вначале найдем сумму квадратов по строкам и из нее найдем среднее квадратичное по строкам. Разности между средним по каждой строке и общим средним вычисляются следующим образом:
dr1 = Mr1 – Мобщ, dr2 = Mr2 – Мобщ (8.2)
или:
dr1 = 173,5 – 215,5 = –42,0, dr2 = 257,5 – 215,5= +42,0.
Сумма квадратов по строкам – это сумма квадратов этих d-значений, умноженная на произведение числа случаев в группе η и числа столбцов с:
СКстр = пc(d2r1+ d2r2) и т. д., если есть последующие строки. (8.3)
Здесь
СКВстр = 172(1764,0 + 176,40) = 119952
Число степеней свободы для строк равно их числу минус 1:
dfстр = r – 1. (8.4)
В нашем случае
dfстр = 2 – 1 = 1.
И здесь также межгрупповое среднее квадратичное находится делением суммы квадратов на число степеней свободы. Поэтому для строк
или:
Среднее квадратичное по столбцам
Совершенно аналогичные процедуры могут быть сделаны и относительно столбцов. Вначале
dc1 = Mc1 – Mобщ, dc2 = Mc2 – Mобщ (8.6)
или:
dc1 = 206,0 – 215,5 = –9,5, dc2 = 225,0 – 215,5 = +9,5,
СКстл = пr(d2c1+ d2c2) и т. д., если есть еще столбцы (8.7)
или:
СКстл = 17 ∙ 2(90,25 + 90,25) = 6137,
dfстл=с – 1 (8.8)
или:
dfстл = 2 – 1 = 1,
В нашем случае
Среднее квадратичное (строки × столбцы)
Для того чтобы найти сумму квадратов (СКстр×стл), вы должны вначале найти разность между средним каждой подгруппы и общим средним, Затем сложить квадраты этих разностей и умножить полученную сумму на число случаев в группе. Наконец, вычесть из этого числа сумму квадратов по строкам и сумму квадратов по столбцам. Давайте теперь проделаем эти операции шаг за шагом:
dr1c1 = Mr1c1 – Mобщ, dr1c2 = Mr1c2 – Mобщ,
dr2c1 = Mr2c1 – Mобщ, dr2c2 = Mr2c2 – Mобщ.
В нашем случае
dr1c1 = 162,0 – 215,5 = – 53,5,
dr1c2 = 185,0 – 215,5= – 30,5, dr2c1 = 250,0 – 215,5 = + 34,5,
dr2c2 = 265,0 – 215,5 = + 49,5,
СКстр×стл = n (d2r1c1 + d2r1c2 + d2r2c1 + d2r2c2) – СКстр – СKстл· (8.10)
(Замечание: первая часть уравнения уже вычислялась с использованием уравнения 7.4.)
СКстр×стл = 17(2862,25 + 930,25 + 1190,25 + 2450,25) – 119952 – 6137 = 126361 – 119952 – 6137 = 272.
Прежде чем мы перейдем к последнему шагу вычисления среднего квадратичного (СКВстр×стл), мы должны найти число степеней свободы для взаимодействия строк и столбцов. Вспомним, что мы сравниваем разности по одной независимой переменной, вызванные действием другой независимой переменной. Существуют (r – 1) разностей по строкам и (с – 1) при сравнении этих строк с разностями по столбцам. Таким образом, общее число df равно произведению (r – 1)(с – 1). В нашем случае, где всего две строки и два столбца, взаимодействие (строки×столбцы) равно 1:
dfстр×стл = (r – 1)(с – 1) (8.11)
или:
dfстр×стл = (2 – 1)(2 – 1) = 1.
Среднее квадратичное по строкам и столбцам равно сумме квадратов по строкам и столбцам, деленное на 13соответствующее число степеней свободы:
В нашем случае
Вычисление F-отношения
Теперь у нас есть четыре оценки популяционной дисперсии σ̅2X. Это (1) внутригрупповое среднее квадратичное; (2) среднее квадратичное по строкам; (3) среднее квадратичное но столбцам и (4) среднее квадратичное – строки×столбцы. Мы можем использовать внутригрупповое среднее квадратичное как знаменатель при вычислении F-отношения относительно каждого из остальных средних квадратичных. Введение знаменателя часто называют показателем ошибки, имея в виду несистематическое изменение, которое невозможно контролировать в экспериментальных условиях:
В нашем случае
Таким же образом,
или:
И еще раз соответственно:
или:
Принятие или отвержение нуль-гипотезы
Аналогично тому, как это делалось в статистическом приложении к главе 7, мы воспользуемся Статистической таблицей 3 для нахождения критического Значения F. Для Fстр имеется 1df в числителе и 64df в знаменателе. Табличное значение для отвержения нуль-гипотезы для 1 и 65df равно 7,04 на уровне 0,01, Очевидно, что полученная нами величина 380,80 позволяет на этом уровне отклонить нуль-гипотезу. Для Fстр комбинация в числителе и знаменателе та же самая. И здесь полученная величина 19,48 позволяет отклонить нуль-гипотезу на альфа-уровне, равном 0,01.
Для Fстр×стл мы также ищем табличное значение для 1 и 65df. Полученная нами величина 0,86 не позволяет отклонить нуль-гипотезу даже для альфа-уров-ня = 0,05. Критическое значение здесь равно 3,99. F, меньшее единицы, может быть получено лишь для выборочного распределения. В этом случае оно просто не может быть статистически значимым.
Таблица дисперсионного анализа
Дисперсионный анализ можно подытожить в виде следующей таблицы. Обратите внимание, что степени свободы являются аддитивными так же, как и суммы квадратов.
Дисперсионный анализ. Эксперимент на время реакции с разными типами стимулов и видами реакций
Задача. Используйте данные из задачи в статистическом приложении к главе 7 и проведите дисперсионный анализ с составлением таблицы дисперсионного анализа. Снова данные получены для шести раздельных групп испытуемых. Одной переменной является величина награды, второй переменной – трудность задачи. Данные из главы 7 должны быть использованы следующим образом.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.56.251 (0.014 с.) |


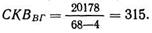
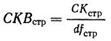 (8.5)
(8.5)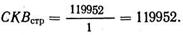
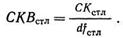 (8.9)
(8.9)
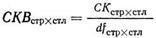 (8.12)
(8.12)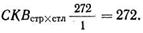
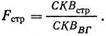 (8.13)
(8.13)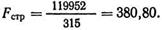
 (8.14)
(8.14)
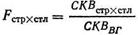 (8.15)
(8.15)



