Три проблемы коэффициента шарпа

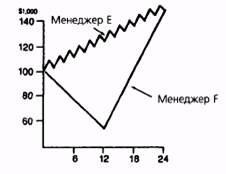
Хотя коэффициент Шарпа — полезный способ измерений, у него есть некоторое количество потенциальных недостатков**

1. Измерение прибыли в коэффициенте Шарпа. Это изме­рение — среднемесячная доходность (или доходность за другой интер­вал времени), выраженная в процентах годовых, — более приспособ­лено для оценки вероятной результативности в следующем месяце, чем для оценки результативности на протяжении всего года. Например, предположим, что управляющий в течение полугода получает 40% при­были каждый месяц, а другие 6 месяцев приносят ему убытки в разме­ре 30%. Вычисляя годовую прибыль, исходя из среднемесячной, мы получим 60% (12 х 5%). Однако если размер позиции корректируется в соответствии с существующими активами, а так поступает большин­ство управляющих, действительная прибыль за год составила бы -11%. Это произойдет, потому что из каждого доллара активов, имеющихся в начале периода, к концу периода осталось бы только $0,8858((1,40)⁶ х (0,70)⁶ = 0,8858).

Как показывает этот пример, если вы озабочены оценкой потенци­альной доходности за расширенный период, а не лишь за следующий месяц или другой интервал, то измерение прибыли, используемое в ко­эффициенте Шарпа, может вести к огромным искажениям. Однако эту проблему можно обойти, используя среднее геометрическое (в проти-

* Здесь подразумевается, что торговые активы постоянны (прибыль изыма-

ется, а убытки восполняются). Другими словами, отсутствует реинвестирова­ние прибыли и снижение величины инвестиций в случае убытков. Вообще го­воря, хотя вычисление прибыли с учетом реинвестиций предпочтительно, это обстоятельство более чем компенсируется существенным преимуществом, со­стоящем в отсутствии необходимости оценивать требования к минимальной величине активов в случае торговой системы. Более того, система с более высокой прибылью, рассчитанной без учета реинвестиций, чаше всего будет демонстрировать и более высокую прибыль с их учетом.

** Этот раздел адаптирован из статьи Дж. Швагера «Alternative to Sharpe Ratio Better Measure of Performance», Futures, p. 57-58, March 1985.

ГЛАВА 21. измерение результативности торговли 739

воположность арифметическому) при расчете средней месячной доход­ности, которую затем выражают в процентах годовых, чтобы получить числитель коэффициента Шарпа. Средняя геометрическая доходность в процентах годовых в точности эквивалентна средней годовой доход­ности с учетом реинвестиций, которая обсуждается позже в этой главе в разделе, посвященном отношению прибыли к максимальному падению стоимости активов.

2. Коэффициент Шарпа не делает различий между коле­-
баниями стоимости активов вверх и вниз. Коэффициент Шарпа
измеряет волатильность, а не риск. А это не обязательно одно и то же.

С точки зрения меры риска, используемой в коэффициенте Шар­па, т.е. стандартного отклонения доходности, колебания вверх и вниз рассматриваются как в равной степени плохие. Таким образом, коэф­фициент Шарпа показывал бы в невыгодном свете управляющего, у которого спорадически наблюдались бы резкие увеличения активов, даже если бы падения стоимости активов были малы.

Рис. 21.3 сравнивает гипотетическое движение активов менедже­ра С, где время от времени наблюдается рост активов и отсутствует их падения, и менеджера D, который столкнулся с несколькими падения­ми стоимости активов. Хотя оба управляющих зафиксировали равную прибыль за период в целом, и менеджер D столкнулся с несколькими отрицательными переоценками, в то время как у менеджера С их не было, коэффициент Шарпа оценил бы менеджера D выше (см. табли­цу). Такой исход — прямое следствие того факта, что коэффициент Шарпа оценивает верхнюю волатильность точно так же, как и нижнюю.

3. Коэффициент Шарпа не делает различий между череду­-
ющимися и последовательными убытками. Мера риска в коэф­-
фициенте Шарпа (стандартное отклонение) не зависит от последова­-
тельности выигрышных и убыточных периодов.

На рис. 21.4 показано гипотетическое изменение стоимости акти­вов с начальной величиной $100 000, управляемых менеджером Е и менеджером F. Каждый из них в обшей сложности зарабатывает $48 000, или $24 000 в год. Однако у менеджера Е месячные доходы в $8000 чередуются с месячными потерями в размере $4000, в то вре­мя как менеджер F сразу теряет $48 000 в первые 12 месяцев и пос­ледовательно зарабатывает $96 000 в течение оставшегося периода.

Коэффициент Шарпа этих двух управляющих был бы одним и тем же. Несмотря на этот факт, мало нашлось бы трейдеров, рассматри­вающих деятельность этих менеджеров как эквивалентную с точки зре­ния риска. Фактически все трейдеры согласились бы с тем, что резуль­таты менеджера F подразумевают значительно более высокий уровень риска.

Рисунок 21.3.

СРАВНЕНИЕ УПРАВЛЯЮЩЕГО С ВЫСОКОЙ ВОЛАТИЛЬНОСТЬЮ, ВЫЗВАННОЙ РЕЗКИМ РОСТОМ АКТИВОВ

ПРИ ОТСУТСТВИИ ПАДЕНИЯ СТОИМОСТИ АКТИВОВ, И УПРАВЛЯЮЩЕГО С ПАДЕНИЯМИ СТОИМОСТИ АКТИВОВ

Рисунок 21 Л.

СРАВНЕНИЕ ДВУХ УПРАВЛЯЮЩИХ С ОДИНАКОВОЙ

ДОХОДНОСТЬЮ И СТАНДАРТНЫМ ОТКЛОНЕНИЕМ, НО С

РАЗЛИЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ МЕСЯЧНЫХ

ПРИБЫЛЕЙ И УБЫТКОВ

Источник: Дж. Швагер «Alternative to Sharpe Ratio Better Measure of Performance», Futures, p. 56, March 1985.

Таблица 21.1.