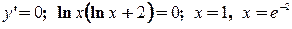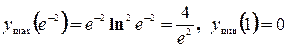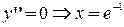Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значения функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Существует два типа задач на нахождение наибольшего и наименьшего значений функции: 1) Наибольшее и наименьшее значения функции, заданной на отрезке 1. найти критические точки 2. выбрать те критические точки, которые лежат внутри 3. найти значения функции на концах отрезка, т.е. 4. из полученных значений функции выбрать наибольшее и наименьшее Пример: Найти наибольшее и наименьшее значения функции Решение: 1.
2.
3. 4. 2) Наибольшее и наименьшее значения функции, заданной на интервале или полуинтервале.
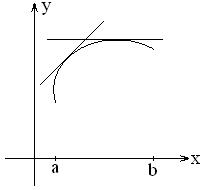
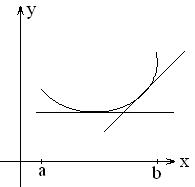
а). На практике, особенно в геометрии, наиболее часто встречаются задачи, когда внутри рассматриваемого промежутка функция имеет только одну точку экстремума. Тогда помогает теорема: Т. Пусть функция б). Если точек экстремума несколько, то: 1). построить график функции 2). если график построить сложно, то необходимо исследовать функцию на экстремум и исследовать поведение функции на концах промежутка, т.е. найти Пример: Найти наименьшее значение функции Решение:
Лекция № 33. Тема: «Выпуклость и вогнутость графика функции. Точки перегиба. Асимптоты». Опр. Кривая выпукла на интервале
Опр. Кривая вогнута на интервале
Достаточные признаки выпуклости и вогнутости графика функции:
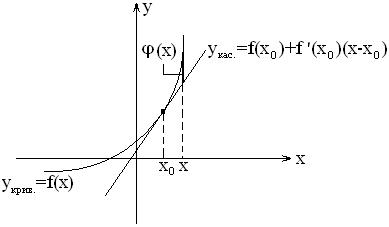
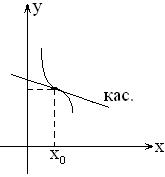
Обозначим отклонение функции от касательной за
Найдем отклонение
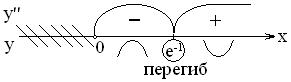
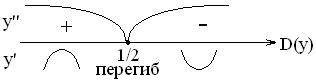
Точка Т. Если (Без док-ва) Пример: Исследовать функцию на выпуклость и вогнутость: Решение:
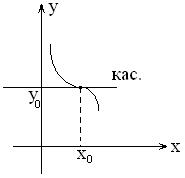
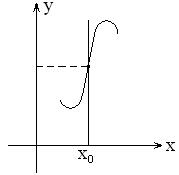
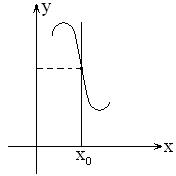
Различные виды точек перегиба
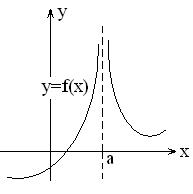
Асимптоты
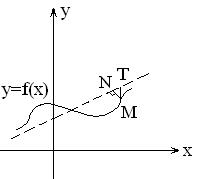
Опр. Асимптотой кривой называется прямая, к которой кривая неограниченно приближается по мере удаления в бесконечность. Как найти асимптоты? 1) Если существует 2) Если 3) Пусть кривая имеет наклонную асимптоту
Т.к. Пример: Найти асимптоты графика функции Решение: 1) Горизонтальная асимптота:
2) Вертикальная асимптота:
3) Наклонная асимптота:
Лекция № 34. Тема: «Полное исследование функции и построение ее графика» 0) Если возможно, построить схематично график функции. 1) Найти область определения функции. 2) Выяснить, является ли функция четной, нечетной, периодической. 3) Исследовать на непрерывность: найти точки разрыва и выяснить их характер. 4) Найти асимптоты графика функции. 5) Найти точки экстремума функции, вычислить значение функции в этих точках. Установить интервалы монотонности. 6) Найти точки перегиба графика функции. Вычислить значение функции в этих точках. Установить интервалы выпуклости и вогнутости. 7) Найти контрольные точки, точки пересечения графика с осями координат. 8) Используя полученный результат, построить график функции. Примеры: I.
1) 2) а). б). Функция ни четная, ни нечетная. 3) Функция непрерывна на всей области определения, как сумма непрерывных функций. 4) Вертикальная асимптота: Горизонтальная асимптота: Наклонная асимптота:
5)
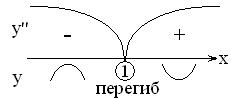
6)
7)
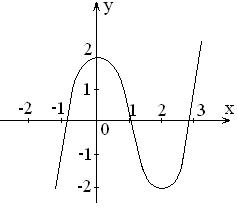
II.
1)
2) Функция ни четная, ни нечетная, т.к. 3) Функция непрерывна на всей 4) Вертикальная асимптота:
Вертикальных асимптот нет. Горизонтальная асимптота: Наклонная асимптота: 5)
6)
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.009 с.) |

 . Чтобы найти наибольшее и наименьшее значения функции, необходимо:
. Чтобы найти наибольшее и наименьшее значения функции, необходимо: и
и 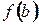
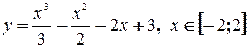


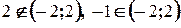
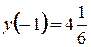
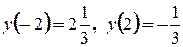


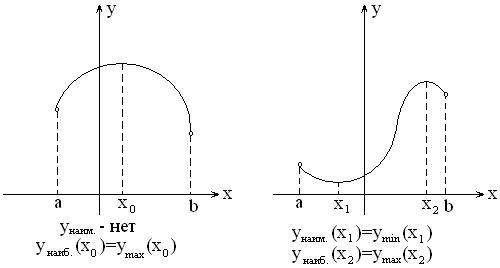
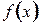 дифференцируема в интервале
дифференцируема в интервале 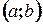 и имеет в этом интервале только одну точку экстремума -
и имеет в этом интервале только одну точку экстремума - 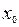 . Если
. Если 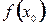 - наибольшее значение функции на
- наибольшее значение функции на  на
на  .
.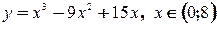
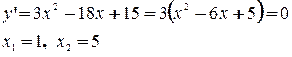


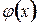 .
.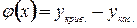
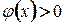 на
на  на
на 
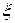 находится между
находится между 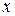 и
и 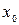 . Итак, отклонение
. Итак, отклонение 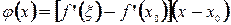 , где
, где  ,
, 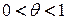 .
.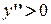 на интервале
на интервале 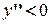 на
на 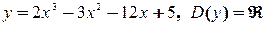 .
.
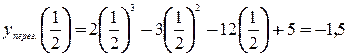

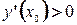



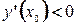


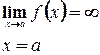

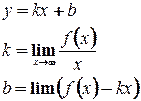
 , то график имеет вертикальную асимптоту, уравнение которой
, то график имеет вертикальную асимптоту, уравнение которой 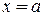 .
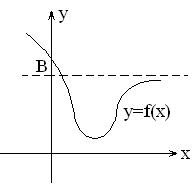
. , то кривая имеет горизонтальную асимптоту, уравнение которой
, то кривая имеет горизонтальную асимптоту, уравнение которой 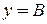
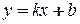 , найдем
, найдем 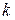 и
и 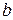 . Кривая приближается к асимптоте, а следовательно
. Кривая приближается к асимптоте, а следовательно 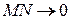 , удобнее рассматривать отрезок
, удобнее рассматривать отрезок 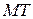 , т.к.
, т.к. 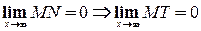 .
. , тогда
, тогда
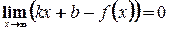 , тогда
, тогда 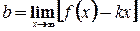
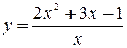
 , горизонтальной асимптоты нет
, горизонтальной асимптоты нет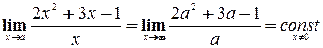
 - вертикальная асимптота
- вертикальная асимптота
 - наклонная асимптота
- наклонная асимптота

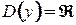
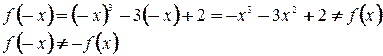
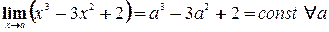 - вертикальных асимптот нет
- вертикальных асимптот нет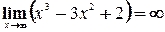 - горизонтальных нет
- горизонтальных нет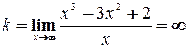 - наклонных нет
- наклонных нет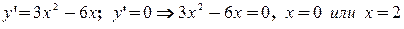 - критические точки.
- критические точки.

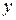 возрастает, когда
возрастает, когда 
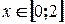
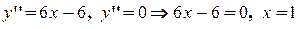
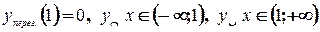
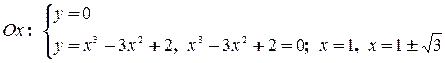
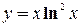

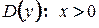

 не является симметричным множеством относительно 0.
не является симметричным множеством относительно 0.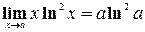
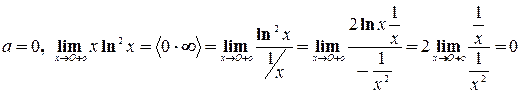
 - горизонтальных асимптот нет.
- горизонтальных асимптот нет. - наклонных асимптот нет
- наклонных асимптот нет