
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заданных неявно и параметрически.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опр. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; например, функция Опр. Функция y аргумента x называется неявной, если она задана уравнением Выше было рассмотрено дифференцирование явных функций, заданных в виде Для нахождения производной функции y, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая y как функцию от x, а затем из полученного уравнения найти производную Пример: Найти производную функции y, заданной уравнением Дифференцируя обе части равенства и учитывая, что y есть функция от x, получим Значение производной при Опр. Говорят, что функция задана параметрически, если зависимость между переменными x и y осуществляется посредством третьей переменной t по формулам: Если x и y рассматривать как координаты точки на плоскости XOY, то при параметрическом задании функции при помощи равенств (1) при изменении параметра t эти точки плоскости описывают некоторую кривую. Про эту кривую говорят, что она задана параметрически. Например, уравнения При параметрическом задании функции, прямая, перпендикулярная к оси абсцисс может пересекать кривую в двух и более точках.
Т. Если функция
Предполагается, что значению t соответствует значение x. Пример: Написать уравнение касательной и нормали к кривой, заданной параметрически уравнениями: Решение. Рассматриваемая кривая представляет собой астроиду.
Найдем точку на этой астроиде, соответствующую значению параметра
Уравнение касательной: Уравнение нормали:
Лекция № 28. Тема: «Логарифмическое дифференцирование. Производные высших порядков. Формула Лейбница. Использование понятия производной в экономике». Рассмотрим функцию Действительно,
Из соотношения
Если же Найдем теперь производную функции
Так как Учитывая полученное равенство, найдем производную функции Дифференцируя сложную функцию, получим:
Отношение Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле:
Для упрощения записи условимся при логарифмическом дифференцировании знак модуля у Пример: Логарифмируя, запишем: Дифференцируя, получим:
Если функция Опр. Производная от производной функции Обозначение: По определению Аналогично определяются третья производная функции,…, n -ная производная функции
Определение n -ной производной дается формулой:
Производные функции второго, третьего и т.д. порядков называются производными этой функции высших порядков. Производная функции второго порядка имеет механическое истолкование: она дает скорость изменения скорости изменения самой функции – это ускорение. Из механики известно, что путь, проходимый телом без сопротивления воздуха, выражается формулой: Производные высших порядков вычисляются по обычным правилам дифференцирования. Операция нахождения производных называется дифференцированием.
Вывод: При дифференцировании любого многочлена получается многочлен, степень которого на единицу меньше, чем степень исходного многочлена. n -ная производная многочлена n -ной степени равняется коэффициенту при старшей степени, умноженному на
С помощью производных можно получить формулу бинома Ньютона:
Предположим, что Предположим, что И т.д. После m раз дифференцирования формулы (1) в полученном равенстве, полагая И т.д. После n раз дифференцирования формулы (1) получаем:
Подставляя в равенство (1) найденные значения коэффициентов, получаем формулу бинома Ньютона. Из этой же формулы при Для вычисления высших производных от произведения двух функций существует формула Лейбница. Если
Экономический смысл производной. Пусть функция Рассмотрим еще одно понятие, иллюстрирующее экономический смысл производной. Издержки производства Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и др. Предельные величины характеризуют не состояние, а процесс, изменение экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции. Опр. Эластичностью функции Эластичность функции показывает приближенно, на сколько процентов изменится функция Лекция № 29. Тема: «Дифференциал функции. Связь дифференциала с производной. Геометрический и механический смысл дифференциала» Пусть функция
В записи формулы (1) слагаемое Опр. Дифференциалом функции Такой дифференциал обозначается так:
Следовательно, по определению дифференциала функции мы должны иметь: Подставляя в равенство (3) вместо дифференциала его выражение (2), получаем: Разделим обе части равенства на
Следовательно, получаем утверждение: если в точке Верно и обратное утверждение: если
По формуле (4) фактически вычисляется дифференциал функции. Возьмем функцию
Дифференциал независимой переменной равняется приращению этой переменной, поэтому формулу (4) можно записать так:
Пусть
Из формулы (5) получается новое обозначение для производной функции: Таким образом, мы имеем для функции Из определения дифференциала и описания главной линейной части приращения функции следует, что дифференциал функции можно определить так: Опр. Дифференциалом функции На основании формулы (4) дифференциал функции можно определить чисто формально: Опр. Дифференциалом функции Выясним геометрический смысл дифференциала функции, используя формулу (4), и учитывая геометрический смысл производной функции.
Из последнего равенства получаем геометрический смысл дифференциала функции. Дифференциал функции Механический смысл дифференциала функции получается из механического истолкования производной функции. Пусть функция
Тема: «Инвариантная форма записи дифференциал. Дифференциалы высших порядков. Применение дифференциала функции к приближенным вычислениям значений функции» Для вычисления дифференциала функции
Дело в том, что в этом случае Пусть имеем функцию
Дифференциал сложной функции вычисляется по формуле (2). Итак, формула (2) применима для вычисления производной функции как в случае, когда Если
Вычисляя дифференциал сложной функции
Должно быть: Пусть функция
В такой записи Опр. Дифференциал от дифференциала функции
Аналогично определяется дифференциал функции Если
Рассмотрим, какие вычислительные формулы получаются для дифференциалов высших порядков. Если
Итак, в случае, когда
Аналогичным образом получаются формулы для вычисления дифференциала третьего и вообще
Формула В этом случае имеем:
Эта формула с формулой (5) не совпадает, так что (5) для дифференциала второго порядка не обладает свойством инвариантности, она не всегда верна. То же самое можно сказать и о дифференциалах третьего и т.д. порядков. Если функция
Если в этом случае пренебречь бесконечно малой величиной
Это равенство означает, что при малых приращениях
Последнее равенство можно записать так:
По этой формуле можно вычислять приближенно значения функции в точках
Лекция № 30. Тема: «Основные теоремы дифференциального исчисления. Раскрытие неопределенностей по правилу Лопиталя». Существует несколько теорем, связанных с производными функций, которые лежат в основе всех применений дифференциального исчисления. Эти теоремы принято называть основными теоремами дифференциального исчисления. Т. (Ферма): Если функция Док-во: Предполагается, что Этот предел не зависит от того, каким образом (справа или слева)
Оба условия (*) и (**) выполняется, когда ч.т.д. Геометрическое истолкование теоремы Ферма получается из геометрического смысла производной. В точке Т. (Ролля): Если функция (Без док-ва)
Геометрическое истолкование теоремы Ролля очевидно.
Все условия теоремы Ролля существенны в формулировке этой теоремы. Например, если функция Пример:
Т. (Лагранжа):): Если функция
Док-во: Рассмотрим вспомогательную функцию: Эта функция непрерывна на отрезке
Из последнего равенства получается равенство (1). ч.т.д. Замечание. Теорема Лагранжа, как видно из ее доказательства, является следствием теоремы Ролля. В свою очередь теорема Ролля получается из теоремы Лагранжа, если Выясним геометрический смысл теоремы Лагранжа.
Дробь правой части равенства (1) представляет собой тангенс угла наклона хорды AB, соединяющей соответствующие точки графика функции
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.237 (0.009 с.) |

 .
. , не разрешенным относительно зависимой переменной; например, функция
, не разрешенным относительно зависимой переменной; например, функция  , заданная уравнением
, заданная уравнением  (заметим, что последнее уравнение задает две функции,
(заметим, что последнее уравнение задает две функции, 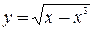 при
при  , и
, и  при
при  ).
). . Рассмотрим дифференцирование неявной функции, заданной уравнением
. Рассмотрим дифференцирование неявной функции, заданной уравнением  .
. , и вычислить ее значение в точке
, и вычислить ее значение в точке  .
. , откуда
, откуда  .
. .
. (1). При этом переменная
(1). При этом переменная  называется параметром.
называется параметром. параметрически задают окружность с центром в начале координат с радиусом R. Если
параметрически задают окружность с центром в начале координат с радиусом R. Если  , соответствующие точки
, соответствующие точки  координатной плоскости описывают эту окружность.
координатной плоскости описывают эту окружность.
 и
и  дифференцируемы и
дифференцируемы и  , то производная
, то производная  вычисляется по формуле:
вычисляется по формуле:
 в точке, соответствующей значению параметра
в точке, соответствующей значению параметра  .
.

 или
или 

 и докажем, что для любого
и докажем, что для любого  .
. При этом
При этом  .
. , учитывая непрерывность логарифмической функции, получаем:
, учитывая непрерывность логарифмической функции, получаем: , и следовательно,
, и следовательно,  .
. , то учитывая равенство
, то учитывая равенство  , получим:
, получим:  .
. . Эта функция определена при всех
. Эта функция определена при всех 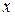 , кроме
, кроме  .
.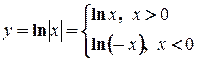
 , то окончательно получаем:
, то окончательно получаем:  .
. или, что то же, функции
или, что то же, функции  , где
, где  . При этом предполагается, что функция
. При этом предполагается, что функция 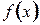 не обращается в ноль в рассматриваемой точке
не обращается в ноль в рассматриваемой точке  , т.е.
, т.е.  (1)
(1) называется логарифмической производной функции
называется логарифмической производной функции 

 .
. , откуда
, откуда
 имеет производную
имеет производную  , то эта производная в свою очередь тоже является функцией и может иметь производную.
, то эта производная в свою очередь тоже является функцией и может иметь производную. .
. .
.

 .
.

 .
.

 - представляет собой многочлен n -ной степени. В общем виде его можно записать так:
- представляет собой многочлен n -ной степени. В общем виде его можно записать так: (1), где
(1), где  - какие-то пока неопределенные числа, коэффициенты.
- какие-то пока неопределенные числа, коэффициенты. . Продифференцируем формулу (1):
. Продифференцируем формулу (1):  (2)
(2) . Продифференцируем формулу (2), в полученном равенстве полагаем, что
. Продифференцируем формулу (2), в полученном равенстве полагаем, что  .
.

 и при
и при  получим известные формулы для квадрата суммы и для куба суммы двух слагаемых.
получим известные формулы для квадрата суммы и для куба суммы двух слагаемых. и эти функции имеют все производные, то имеет место формула Лейбница:
и эти функции имеют все производные, то имеет место формула Лейбница:

 выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент
выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент  . Очевидно, за период времени от
. Очевидно, за период времени от  количество произведенной продукции изменится от значения
количество произведенной продукции изменится от значения  до значения
до значения  ; тогда средняя производительность труда за этот период времени
; тогда средняя производительность труда за этот период времени  . Очевидно, что производительность труда в момент
. Очевидно, что производительность труда в момент  , т.е.
, т.е.  .
.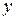 будем рассматривать как функцию количества выпускаемой продукции
будем рассматривать как функцию количества выпускаемой продукции  - прирост продукции, тогда
- прирост продукции, тогда  - приращение издержек производства и
- приращение издержек производства и  - среднее приращение издержек производства на единицу продукции. Производная
- среднее приращение издержек производства на единицу продукции. Производная  выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции. называется предел отношения относительного приращения функции
называется предел отношения относительного приращения функции 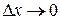 :
: 
 такова, что при переходе от точки
такова, что при переходе от точки  к точке
к точке  получает приращение, которое представляется так:
получает приращение, которое представляется так:
 (1)
(1) не зависит от
не зависит от  - бесконечно малая величина высшего порядка малости по сравнению с
- бесконечно малая величина высшего порядка малости по сравнению с  .
. при
при 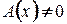 называется главной линейной частью приращения функции, т.е. величина
называется главной линейной частью приращения функции, т.е. величина  .
.
 (2)
(2) или
или  (3)
(3)
 .
. , то по связи между функцией, имеющей предел в точке, и бесконечно малой величиной в этой точке имеем:
, то по связи между функцией, имеющей предел в точке, и бесконечно малой величиной в этой точке имеем: , где
, где  - бесконечно малая величина при
- бесконечно малая величина при  , а это и означает, что функция в точке
, а это и означает, что функция в точке  (4)
(4) , вычислим дифференциал по формуле (4):
, вычислим дифференциал по формуле (4):
 (5)
(5) . Вычислим дифференциал по определению:
. Вычислим дифференциал по определению:
 .
. .
.

 .
. выражает закон прямолинейного движения точки, тогда
выражает закон прямолинейного движения точки, тогда  - есть скорость движения в момент времени t. Дифференциал:
- есть скорость движения в момент времени t. Дифференциал:  , где
, где  - некоторый промежуток времени. Из этого равенства и получаем механическое истолкование дифференциала функции. Дифференциал функции, выражающей закон прямолинейного движения, представляет собой длину пути, который точка прошла бы, если бы она за промежуток времени
- некоторый промежуток времени. Из этого равенства и получаем механическое истолкование дифференциала функции. Дифференциал функции, выражающей закон прямолинейного движения, представляет собой длину пути, который точка прошла бы, если бы она за промежуток времени  . Оказывается, что формула (2) остается верной и в том случае, когда
. Оказывается, что формула (2) остается верной и в том случае, когда  . В этом случае имеем функцию
. В этом случае имеем функцию  . Вычислим дифференциал этой сложной функции по формуле, имеем:
. Вычислим дифференциал этой сложной функции по формуле, имеем:


 . Значит, формула (1) применима только в том случае, когда
. Значит, формула (1) применима только в том случае, когда  имеет все производные. Тогда эта функция имеет дифференциал:
имеет все производные. Тогда эта функция имеет дифференциал: .
. (3)
(3) -ного порядка.
-ного порядка. , то общее определение дифференциала
, то общее определение дифференциала  (4)
(4)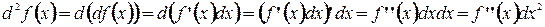
 (5)
(5)
 (6)
(6)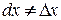 , а
, а  .
.



 или
или  (*)
(*) , то из равенства (*) получаем:
, то из равенства (*) получаем:  . Заменяя
. Заменяя  .
.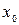 и в этой точке принимает наибольшее или наименьшее значение, то
и в этой точке принимает наибольшее или наименьшее значение, то  , если только эта производная существует.
, если только эта производная существует.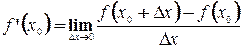 .
.
 [числитель дроби неположителен, знаменатель тоже, значит дробь неотрицательна]
[числитель дроби неположителен, знаменатель тоже, значит дробь неотрицательна] 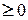 .
.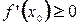 (*)
(*)

 (**)
(**) .
. , дифференцируема на интервале
, дифференцируема на интервале  и
и  , то существует по крайней мере одна точка
, то существует по крайней мере одна точка  , что
, что  .
.
 на
на  . У графика этой функции нет касательных.
. У графика этой функции нет касательных.
 (1)
(1) .
. . Так что для функции
. Так что для функции  выполняются все условия теоремы Ролля, т.е. существует
выполняются все условия теоремы Ролля, т.е. существует  .
.





