
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные формы записи теоремы ЛагранжаСодержание книги
Поиск на нашем сайте
Пусть
(*) – формула приращений Следствие из теоремы Лагранжа: Если функция Док-во: Пусть
ч.т.д. Т. (Коши): Пусть функции
(Без док-ва)
Правило Лопиталя. Т. Пусть функции Док-во: Значения функций в точке a нас не интересует, а
Таким образом: ч.т.д. Замечание: Правило Лопиталя остается справедливым и при Помни! 1) Правило Лопиталя действует, если неопределенность двух типов: 2) Правило Лопиталя в случае других видов неопределенностей 1) неопределенность «
2) неопределенности « С помощью логарифмирования выражения можно свести к неопределенности
Пример:
Лекция № 31. Тема: «Формула Тейлора: для многочлена, для произвольной функции, для некоторых элементарных функций» 1) Формула Тейлора для многочлена. Рассмотрим многочлен степени n:
Разложим данный многочлен по степеням
Положим
Разложение по степеням
Это формула Тейлора для многочлена. Пример: Разложить
Ответ:
2) Формула Тейлора для произвольной функции Пусть функция Опр. Многочленом Тейлора для функции
Например,
Таким образом, Очевидно, если Отметим, что
Учитывая, что
Будем искать остаток
Таким образом,
Итак,
Если положить в формуле Тейлора а =0, то получим формулу Маклорена: Частные случаи формулы Тейлора
3) Формула Тейлора для некоторых элементарных функций а).
б).
в).
г).
Лекция № 32. Тема: «Возрастание и убывание функции. Точки экстремума. Наибольшее и наименьшее значения функции». Т. (достаточное условие возрастания и убывания функции): Если функция Док-во: 1) Нужно доказать, что
Итак, взяли 2) При ч.т.д. Замечание: Иногда бывает, что Например,
Пример: Найти промежутки возрастания и убывания функции 1) Найти 2) Исследовать знак производной:
Ответ:
Экстремумы Опр. Точка Опр. Точка Т. (необходимое условие экстремума): Если функция Док-во: Чтобы убедиться в справедливости этой теоремы, достаточно применить теорему Ферма к той окрестности, о которой говорится в определении экстремума. ч.т.д. Замечание: Обратное утверждение неверно, например, Опр. Точки, в которых производная равна нулю либо не существует, называются критическими. Опр. Точки, в которых производная равна нулю, называются стационарными. Из необходимого условия экстремума следует, что подозрительными на экстремум являются критические точки. Т. (первое достаточное условие экстремума): Если производная функции, непрерывной в точке (Без док-ва) Т. (второе достаточное условие экстремума): ТОЛЬКО ДЛЯ СТАЦИОНАРНЫХ ТОЧЕК! Пусть точка (Без док-ва)
Пример: Исследовать на экстремум функцию Решение:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.190.6 (0.01 с.) |

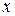 - фиксированная точка,
- фиксированная точка,  - приращенная точка, где
- приращенная точка, где  - произвольное приращение.
- произвольное приращение.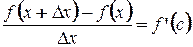
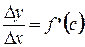 , т.е. отношение приращения функции к приращению аргумента есть значение производной в некоторой промежуточной точке.
, т.е. отношение приращения функции к приращению аргумента есть значение производной в некоторой промежуточной точке.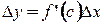
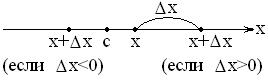
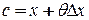 , где
, где  - число от нуля до единицы
- число от нуля до единицы
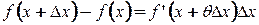 (*)
(*)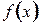 во всех точках промежутка имеет производную, равную нулю, то функция постоянна в этом промежутке.
во всех точках промежутка имеет производную, равную нулю, то функция постоянна в этом промежутке. и
и  - произвольные точки промежутка. Тогда по теореме Лагранжа:
- произвольные точки промежутка. Тогда по теореме Лагранжа: 

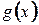 непрерывны на отрезке
непрерывны на отрезке  , дифференцируемы на интервале
, дифференцируемы на интервале  , причем
, причем  для всех
для всех  . Тогда внутри данного отрезка найдется хотя бы одна точка
. Тогда внутри данного отрезка найдется хотя бы одна точка  такая, что выполняется равенство:
такая, что выполняется равенство:
 . Тогда, если существует предел отношения
. Тогда, если существует предел отношения  производных в этой точке, то существует и предел отношения функций, причем имеет место равенство
производных в этой точке, то существует и предел отношения функций, причем имеет место равенство  .
. не изменится, если функции доопределить в точке а, предположив, что
не изменится, если функции доопределить в точке а, предположив, что 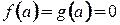 . Рассмотрим предел:
. Рассмотрим предел: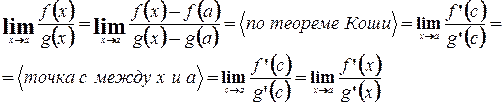

 и при неопределенности
и при неопределенности 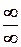 .
.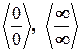

 »
»

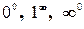 »
» или
или  .
.
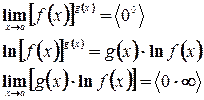

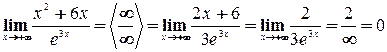
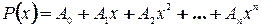
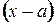 , т.е.
, т.е.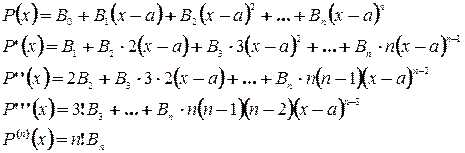
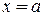 , тогда
, тогда 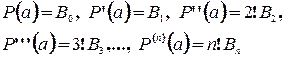 . Таким образом:
. Таким образом:
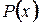 примет вид:
примет вид:
 по степеням
по степеням  .
.


 порядка и пусть x – произвольная точка из окрестности точки а.
порядка и пусть x – произвольная точка из окрестности точки а. -ной степени вида:
-ной степени вида:
 . Рассмотрим а =0. Тогда
. Рассмотрим а =0. Тогда  .
. .
. , где
, где  - остаточный член.
- остаточный член.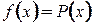 , то
, то  .
.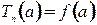

 , получим:
, получим:
 , поэтому
, поэтому  .
. . Найдем множитель
. Найдем множитель 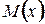 , для этого выясним, что из себя представляет отношение:
, для этого выясним, что из себя представляет отношение: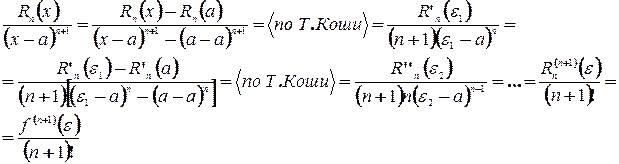
 , где
, где 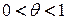 .
. - остаточный член формулы Тейлора в форме Лагранжа.
- остаточный член формулы Тейлора в форме Лагранжа.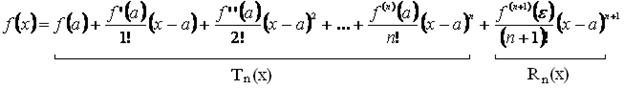





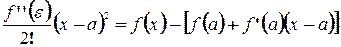 , где
, где  , а
, а 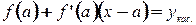

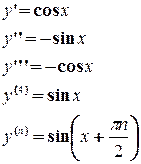
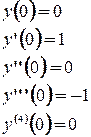




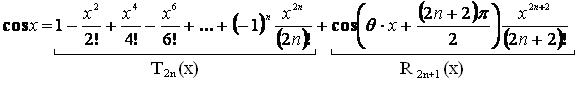



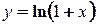



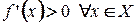
 . Возьмем любые элементы
. Возьмем любые элементы 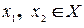 и пусть
и пусть  . Рассмотрим функцию
. Рассмотрим функцию  , применим теорему Лагранжа:
, применим теорему Лагранжа: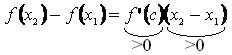

 - возрастает на промежутке X.
- возрастает на промежутке X. на промежутке X теорема доказывается аналогично.
на промежутке X теорема доказывается аналогично. в случае строгого возрастания функции. Это возможно тогда, когда
в случае строгого возрастания функции. Это возможно тогда, когда  в точках, не заполняющих сплошь некоторый промежуток.
в точках, не заполняющих сплошь некоторый промежуток. .
.  .
. в точке
в точке  - одна точка.
- одна точка. .
. 
 :
: 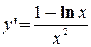


 и убывает, если
и убывает, если 
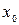 называется точкой максимума непрерывной функции
называется точкой максимума непрерывной функции  , в которой наибольшее значение данной функции достигается в точке
, в которой наибольшее значение данной функции достигается в точке  , для
, для  , для
, для  при
при 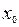 является стационарной для дважды дифференцируемой в окрестности этой точки функции, причем
является стационарной для дважды дифференцируемой в окрестности этой точки функции, причем  . Тогда
. Тогда  , и точкой минимума, если
, и точкой минимума, если  .
.






