
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностей совместных событийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
где Теорема может быть обобщена на любое конечное число совместных событий:
Событие
Условнойвероятностью события А при наличии В называется вероятность события События
Теорема умножения вероятностей независимых событий Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Для большего числа событий, независимых в совокупности:
Теорема умножения вероятностей зависимых событий Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
Пример 1. Зависимы или независимы: 1) несовместные события; 2) события, образующие полную группу; 3) равновозможные события? Решение. 1) Зависимы, так как появление любого из них обращает в нуль вероятности всех остальных; 2) зависимы, так как непоявление всех, кроме одного, обращает в единицу вероятность последнего; 3) могут быть как зависимы, так и независимы.
Пример 2. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются события:
Зависимы или независимы следующие пары событий: 1) Решение. 1) независимы, так как 2) зависимы, так как 3) зависимы, так как 4) независимы, так как 5) зависимы, так как несовместны.
Пример 3. На стеллаже в библиотеке в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие Решение. Первый способ. Событие
По теореме сложения
Окончательно получим
Второй способ. События
Вероятность
Пример 4. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта. Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В. Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого. Всего в колоде 13 червонных и 13 бубновых карт. При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна Тогда
Пример 5. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей? Вероятность выпадения 6 очков при одном броске кости равна
Пример 6. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна
Вероятность того, что второй стрелок попадет в цель, а первый – нет равна
Тогда вероятность попадания в цель только одним стрелком равна
Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:
Тогда вероятность того, что в цель попадет только один стрелок равна:
Пример 7. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.
а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна
Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках.
б) Вероятность того, что нужная деталь находится не менее, чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность равна вероятности того, что деталь не находится только в одном ящике и имеется вообще.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 896; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 ,
, – произведение событий
– произведение событий  и
и  .
. .
. называется противоположным событию
называется противоположным событию  . Сумма вероятностей противоположных событий равна единице:
. Сумма вероятностей противоположных событий равна единице: .
. или
или  .
. ;
;  .
. .
. .
.
 – появление бубнового туза;
– появление бубнового туза; – появление десятки.
– появление десятки. ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
; .
.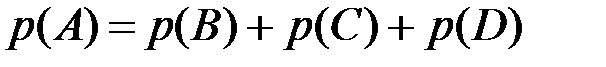 ,
, ,
,  ,
,  .
.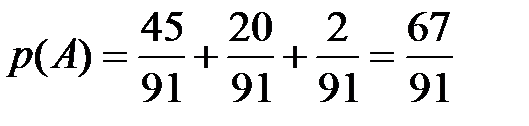 .
. (ни один из взятых трех учебников не имеет переплета) – противоположные, поэтому
(ни один из взятых трех учебников не имеет переплета) – противоположные, поэтому .
. .
. , при вытаскивании второй карты -
, при вытаскивании второй карты -  , третьей -
, третьей -  , четвертой -
, четвертой -  .
. .
. .
. . Вероятность того, что не выпадет 6 очков -
. Вероятность того, что не выпадет 6 очков -  . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна
. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна  . Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна
. Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна  .
. , промах второго – событие
, промах второго – событие  .
.
 .
. .
. .
.


 .
.


