
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы математической статистикиСодержание книги Поиск на нашем сайте
Математическая статистика — раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей. Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Полученные в результате наблюдения (опыта, эксперимента) данные сначала надо обработать: 1) упорядочить, представить в удобном для обозрения и анализа виде. 2)оценить, хотя бы приблизительно, интересующие нас характеристики наблюдаемой случайной величины. Например, дать оценку неизвестной вероятности события, оценку математического ожидания, оценку дисперсии случайной величины, оценку параметров распределения, вид которого неизвестен, и т.д. 3)проверка статистических гипотез, то есть решение вопроса согласования результатов оценивания с опытными данными. Например, выдвигается гипотеза, что наблюдаемая случайная величина подчиняется нормальному закону или случайное событие обладает данной вероятностью. Одной из важнейших задач математической статистики является разработка методов, позволяющих по результатам обследования выборки (т. е. части исследуемой совокупности объектов) делать обоснованные выводы о распределении признака изучаемых объектов по всей совокупности. Для обработки статистических данных созданы специальные программные пакеты (STADIA, SYSTAT, STAT-GRAPHICS и др.). Простейшие статистические функции имеются в программируемых калькуляторах и офисных программах (EXCEL). Результаты исследования статистических данных методами математической статистики используются для принятия решения, т.е. для научных и практических выводов. 1. Генеральная совокупность и выборка. Пусть требуется изучить множество однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным — контролируемый размер детали. Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов. Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью (случайной величиной X). Множество объектов, случайно отобранных из генеральной совокупности ( Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки. Все объекты генеральной совокупности должны иметь одинаковую вероятность попасть в выборку, т. е. выбор должен производится случайно. Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 — объем генеральной совокупности, а 10 — объем выборки.
2. Статистическое распределение выборки. Полигон. Гистограмма. Рассмотрим эксперимент, описание которого строится при помощи случайной величины X. Это означает, что однократный эксперимент дает нам возможность определить одно из возможных значений случайной величины X. Пусть в результате
Отметим, что сумма относительных частот равна единице:
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал. Для графического изображения статистического распределения используются полигоны и гистограммы. Для построения полигона на оси Ох откладывают значения вариант
Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала
Пример. Построить гистограмму частот по данному распределению выборки объема
>
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

 ), называется выборкой.
), называется выборкой. экспериментов получен набор значений случайной величины X:
экспериментов получен набор значений случайной величины X:  ,
,  ,...
,...  . То есть, из генеральной совокупности извлечена выборка, причем
. То есть, из генеральной совокупности извлечена выборка, причем  раз,
раз,  —
—  раз,
раз,  раз и
раз и  — объем выборки. Наблюдаемые значения
— объем выборки. Наблюдаемые значения  называют частотами, а их отношения к объему выборки относительными частотами:
называют частотами, а их отношения к объему выборки относительными частотами: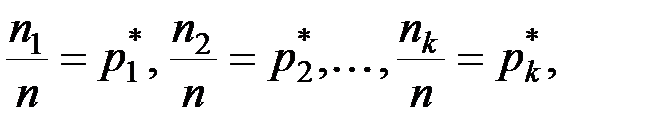

 , на оси Оу — значения частот
, на оси Оу — значения частот  (относительных частот
(относительных частот  ). Точки соединяем ломаной.
). Точки соединяем ломаной. — сумму частот вариант, попавших в i-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами
— сумму частот вариант, попавших в i-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами  (плотность частоты). Площадь i -го частичного прямоугольника равна
(плотность частоты). Площадь i -го частичного прямоугольника равна  . Следовательно, площадь гистограммы равна сумме всех частот, т. е. объему выборки (или единице).
. Следовательно, площадь гистограммы равна сумме всех частот, т. е. объему выборки (или единице). :
:




