
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суть и порядок исчисления средних величинСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Средние величины являются одними из наиболее распространенных обобщающих статистических показателей. Они имеют своей целью одним числом охарактеризовать статистическую совокупность состоящую из меньшинства единиц. Средние величины тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность. С помощью метода средних решаются следующие основные задачи: 1. Характеристика уровня развития явлений. 2. Сравнение двух или нескольких уровней. 3. Изучение взаимосвязей социально-экономических явлений. Анализ размещения социально-экономических явлений в пространстве. Для решения этих задач статистическая методология разработала различные виды средних. Средняя гармоническая является первообразной формой средней арифметической. Она рассчитывается в тех случаях, когда веса fi не заданы непосредственно, а входят как сомножитель в один из имеющихся показателей. Также как и арифметическая, средняя гармоническая может быть простой и взвешанной. Средняя гармоническая простая:
Средняя гармоническая смешанная:
Wi - произведение вариантов на частоты При расчете средних величин необходимо помнить о том, что всякие промежуточные вычисления должны приводить как в числителе, так и в знаменателе и имеющим экономический смысл показателям. Для выяснения методики расчета средней арифметической используем следующие обозначения: X - арифметический признак X (X1, X2,... X3) - варианты определенного признака n - число единиц совокупности
В зависимости от исходных данных средняя арифметическая может быть рассчитана двумя способами: 1. Если данные статистического наблюдения на сгруппированы, или сгруппированные варианты имеют одинаковые частоты, то рассчитывается средняя арифметическая простая:
2. Если частоты сгруппированы в данных разные, то рассчитывается среднее арифметическое взвешанное:
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах. В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот. В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному. В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ. Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше. Если веса fi заданы не в абсолютных показателях, а в относительных, то формула расчета средней арифметической будет следующей:
pi - относительные величины структуры, показывающие, какой процент составляют частоты вариантов в сумме всех частот. Если относительные величины структуры заданы не в процентах, а в долях, то среднее арифметическое будет рассчитываться по формуле:
Мода и медиана в статистике Структурное среднее характеризует состав статистической совокупности по одному из варьирующих признаков. К этим средним относятся мода и медиана. Мода - такое значение варьирующего признака, которое в данном ряду распределения имеет наибольшую частоту. В дискретных рядах распределений мода определяется визуально. Сначала определяется наибольшая частота, а по ней модальное значение признака. В интервальных рядах для вычисления моды используется следующая формула:
Xmo - нижняя граница модальности (интервал ряда с наибольшей частотой) Mo - величина интервала fMo - частота модального интервала fMo-1 - частота интервала предшествующего модальному fMo+1 - частота интервала следующего за модальным Медианой называется такое значение варьирующего признака, которое делит ряд распределения на две равные части по объему частот. Медиана рассчитывается по разному в дискретных и интервальных рядах. 1. Если ряд распределения дискретный и состоит из четного числа членов, то медиана определяется как средняя величина из двух серединных значений рангированного ряда признаков. 2. Если в дискретном ряду распределения нечетное число уровней, то медианой будет серединное значение рангированного ряда признаков. В интервальных рядах медиана определяется по формуле:
Me - величина интервала
Вариация и ее показатели Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может бьпъ одинакрвои, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом — эти отличия велики, т.е. в одном случае вариация признака мала, а в другом - велика, это имеет весьма важное значение для характеристики надежности средней величины. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации. Самым элементарным показателем вариации признака является размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака: R=Xmax-Xmin Среднее линейное отклонение d‾ представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: (х - x‾). Среднее линейное отклонение: для несгруппированных данных d = ∑ | x-x‾| / n где п — число членов ряда; для сгруппированных данных d ‾ =∑ | x-x‾| f / ∑ f где ∑f - сумма частот вариационного ряда. Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):1) простая дисперсия для несгруппированных данных σ2=∑(X-X‾)2 / n 2)взвешенная дисперсия для вариационного ряда σ2=∑(X-X‾)2 f / ∑f Cвойства дисперсии: 1)если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 раз.Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
где а — дисперсия, исчисленная по способу моментов; i— величина интервала; x1=x-A/ i новые (преобразованные) значения вариантов (А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой); — момент второго порядка; — квадрат момента первого порядка Среднее квадратическое отклонение σ равно корню квад-| ратному из дисперсии: для несгруппированных данных
для вариационного ряда
Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные ва- рианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется. Обозначим: 1 — наличие интересующего нас признака; 0 — его отсутствие; р — доля единиц, обладающих данным признаком; q — доля единиц, не обладающих данным признаком; р + q =1. Исчислим среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака так как p + q = l.,то
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 925; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.207.112 (0.011 с.) |


 - средняя величина признака
- средняя величина признака

 - численность (частоты) вариантов
- численность (частоты) вариантов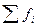 - сумма частот
- сумма частот



 - нижняя граница медианного интервала (интервала для которого накопленная частота впервые превысит полусумму частот)
- нижняя граница медианного интервала (интервала для которого накопленная частота впервые превысит полусумму частот)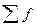 - сумма частот ряда
- сумма частот ряда - сумма накопленных частот предшествующих медианному интервалу
- сумма накопленных частот предшествующих медианному интервалу - частота медианного интервала
- частота медианного интервала






