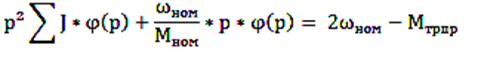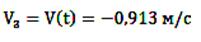Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения движения. Двухмассовая механическая системаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис.3.1. Расчетная схема двухмассовой механической системы Расчетная схема двухмассовой системы. Система (рис. 3.1, а) содержит две вращающиеся массы с моментами инерции J1 и J2, связанные упругим звеном с жесткостью с. К первой массе (пусть это будет ротор двигателя) приложены моменты М, который примем пока постоянным, и Mc1, обусловленный, например, трением. Вторую массу будем полагать нагруженной статическим моментом Мс2. В статическом режиме, как отмечалось, все элементы системы будут двигаться с одинаковой скоростью, в динамическом же в силу наличия упругости скорости будут различны: ω1 – у первой массы и ω1 – у второй. Математическая модель. Поставим задачу – записать уравнения движения такой идеализированной двухмассовой системы. Расчленим систему на части (рис. 3.1, 6) и заменим каждую отброшенную часть ее реакцией, как это всегда делается в механике при составлении уравнений равновесия. Реакцию упругого элемента представим моментом упругого взаимодействия М12:
Для первой и второй масс на основании второго закона Ньютона записываем, соблюдая знаки моментов:
Уравнения (3.1) — (3.3) составляют полное математическое описание системы на рис. 3.1, а. Весь вопрос теперь в том, как распорядиться этим описанием, а это зависит от того, какие задачи нужно решать. Простые частные случаи. Пусть моменты сопротивления пренебрежимо малы
В коэффициенте перед третьей производной скорости легко узнать частоту собственных колебаний
а в правой части – среднее ускорение εср. Тогда окончательно будем иметь
Как и следовало ожидать, уравнение описывает незатухающий колебательный процесс (корни характеристического уравнения p1 = 0, p2,3 = ±jΩ12) с частотой колебаний Ω12. Оно определяет изменение средней скорости εсрt, на которую колебания накладываются. Решение уравнения (3.5) с учетом конкретных начальных условий дает полную картину движения первой массы. Так, при
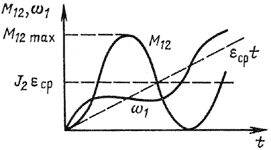
Зависимость ω1 от t показана на рис. 3.2.
Рис. 3.2. Динамические процессы в двухмассовой системе Динамические перегрузки. Математическое описание в виде (3.1) - (3.3) позволяет решать и другие задачи. Например, иногда очень важно оценить динамическую нагрузку упругого звена, т. е. найти и проанализировать зависимость М12 от времени. Решив исходные уравнения (3.1) - (3.3) относительно М12, получим
Это также уравнение незатухающего колебательного процесса, решение которого можно получить в виде
Зависимость M12(t) показана на рис. 3.2. Из нее следует, в частности, что в рассматриваемом случае максимальная нагрузка М12тах вдвое превышает среднюю, определяемую средним ускорением.
В них содержатся переменные (это все М и ω), параметры (с, J1 и J2) и оператор р, причем каждая переменная может быть выражена через другие переменные и параметры в сочетании с операторами. Уравнению (3.8), решенному относительно ω1, будет соответствовать, уравнению (3.7), решенному относительно M12,. Расчеты электромеханической системы. Выбираем реечный двигатель. Исходя из параметров двигателя выбираем: Диаметр вала = 0,003 м. Высота зуба = 0,002 м. Диаметр шестерни = 0,007 м. Рассчитываем коэффициент передачи: Скорость вращения номинальная:
Скорость вращения ведущей шестерни:
Коэффициент передачи:
Момент инерции:
Момент инерции приведения:
Момент трения:
Момент приведения трения:
Источник момента при использовании ИП генератора тока:
Результатом решения данного уравнения является:
В режиме источника напряжения:
Решение:
Учтем, что ω= ̇ и сделаем замену
По заданному графику движения груза рассчитываем:
Найдем время возврата в исходное состояние:
Примем время торможения равное 10% от t5-7, оно будет равно 1,5 сек. Рассчитаем скорость на стадии возврата в исходное состояние, учитывая, что оно будет отрицательным. Рассчитываем:
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.242.56 (0.01 с.) |


 (3.1)
(3.1) (3.2)
(3.2)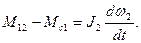 (3.3)
(3.3) и нас интересует движение первой массы. Преобразуем уравнения (3.1) - (3.3), сохранив ω1, и получим
и нас интересует движение первой массы. Преобразуем уравнения (3.1) - (3.3), сохранив ω1, и получим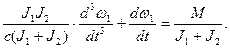
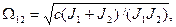 (3.4)
(3.4)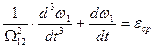 . (3.5)
. (3.5) имеем
имеем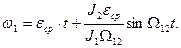
 . (3.6)
. (3.6)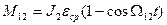 .
.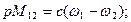 (3.7)
(3.7)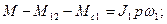 (3.8)
(3.8)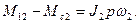 (3.9)
(3.9)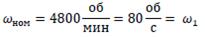

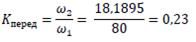
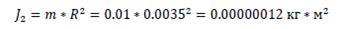
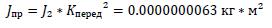
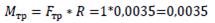
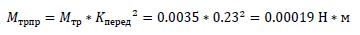
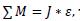 тогда получим равенство:
тогда получим равенство:
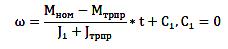

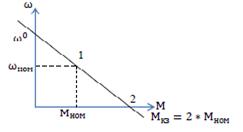
 учитывая, что ω = 2ωном, подставляем в равенство:
учитывая, что ω = 2ωном, подставляем в равенство: