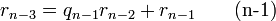Декартів добуток множин не підчинається і сполучному закону, але пов'язаний з операцією об’єднання множин розподільною властивістю : для будь – яких множин А, в і с маємо рівність

Класифікація – це дія розподілу об’єктів по класах на основі схожості об’єктів інших об’єктів. Множина х розбита на класи, якщо: 1. підмножина попарно не перетинається 2. об’єднання підмножин утворює множину х Якщо не виконується хоча б одна з цих вимог, класифікація вважається неправильною. Так, множина Х трикутників можна розбити на 3 класи: гострокутні, прямокутні, тупокутні. Вірно, виділені підмножини попарно не перетинаються(серед гострокутних немає тупокутних і прямокутних, серед прямокутних немає гострокутних і тупокутних тощо) і їх об’єднання співпадає з множиною Х. Проте не кожна система підмножин даної множини являє собою розбиття цієї множини. Наприклад, якщо з множини Х трикутників виділити підмножини рівнобедрених,рівносторонніх і різносторонніх, то розбиття множини Х на класи ми не отримаємо, оскільки множина рівнобедрених, і рівносторонніх трикутників перетинаються (всі ріностороні трикутники являються рівнобедреними). Для того щоб виділити підмножину достатньо вказати характеристичні властивості його елементів.

Розглянемо, наприклад, множину натуральних чисел. Його елементи володіють різними властивостями. Серед натуральних чисел є парні, непарні, кратні 3, кратні 5 тощо. Припустимо, що нас цікавлять числа, що володіють властивістю ділитися на 3. ця властивість дозволяє виділити з множини натуральних чисел підмножину чисел, кратних 3. тоді про інші числа ми можемо сказати, що вони не кратні 3, отже отримуємо ще одну підмножину множини натуральних чисел. Виділені підмножини не перетинаються, а їх об’єднання співпадає з множиною натуральних чисел. Таким чином, задання одних властивостей елементів множини натуральних чисел привело до розбиття цієї множини на 2 класа: клас чисел, кратних 3 (3,6,15), і клас чисел, не кратних 3 (2,4,5,7). А яким буде розбиття на класи, якщо вказати 2 властивості, тобто виділити з множини 2 різні підмножини? Розглянемо 2 властивості натуральних чисел: «бути кратним 3» і «бути кратним 5». За допомогою цих властивостей із множини натуральних чисел можна виділити 2 підмножини: А – підмножина чисел кратних 3, В – підмножина чисел кратних 5. ці підмножини перетинаються, але ні одне з них не являється підмножиною іншого. Проаналізуємо те, що вийшло. Круг, що зображає множину натуральних чисел, розбився на 4 області, що перетинаються – вони пронумеровані. Кожна область зображає деякі підмножини множини натуральних чисел. Підмножина 1 складається з чисел кратних 3,5. підмножина 2 – кратних 3, і не кратних 5. підмножина 3 – кратних 5 і не кратних 3. підмножина 4 – числа, що не кратні ні 3, ні 5. поєднує ці 4 підмножини множина натуральних чисел. Таким чином, виділення 2 властивостей натуральних чисел призвело до розбиття множини на 4 класи. Але так буває не завжди.

10.Декартів добуток. Кортеж. Число елементів декартового добутку.

Декартовим добутком множин А і В називається множина, елементами якої є всі упорядковані пари (а, b) такі, що перший компонент яких єналежить множині А, а другий компонент належить множині В.

Позначається декартів добуток А×В (але не А∙В або АВ).

Нехай А ={a1, a2, a3} i B = {b1, b2}. Знайдемо А×В і В×А.

А×В = {(a1, b1), (a1, b2), (a2, b1), (a2, b2),(a3, b1), (a3, b2)},

B×A = {(b1, a1), (b1, a2), (b1, a3), (b2, a1), (b2, a2), (b2, a3)}.

Із означення видно, що декартів добуток не має переставної властивості: А×В ≠ В×А

Переставна властивість декартового добутку двох різних множин має місце лише тоді, коли одна з них порожня: А×Ø = Ø×А = Ø

Декартів добуток двох рівних множин називають декартовим квадратом: А×А = А2, трьох множин – декартовим кубом і т. д.

Декартів добуток множин не підчинається і сполучному закону, але пов'язаний з операцією об’єднання множин розподільною властивістю: для будь – яких множин А, В і С маємо рівність

Елементи декартового добутку 2 кінчених множин краще записувати за допомогою таблиці. Наприклад. А= (1,2,3) В = (3,5)

А/В

(1,3)

(1,5)

(2,3)

(2,5)

(3,3)

(3,5)

В математиці розглядають не тільки упорядковані пари, а й упорядковані набори з 3, 4 і тощо елементів. Такі набори ще називають кортежами. Так (1,2,3) – кортеж довжиною 3 (так як в ньому 3 елементи), а (7,6,5,4,9) – кортеж довжиною 5.

Декартів добуток множин називається множиною кортежів довжиною n, утворені так, що перший компонент кортежу належить множині, 2- множині, n-я – множині.

Знайдемо декартів добуток множин, якщо = (2,3), =(3,4,5), =(7,8).

Елементами декартового добутку будуть кортежі довжиною 3, сформовані так: перший компонент буде вибиратися з множини, 2 -, 3 -. Отримаємо =((2,3,7); (2,4,8); (2,5,7); (2,5,8); (3,3,7); (3,3,8);(3,4,7);(3,4,8); (3,5,7);(3,5,8)).

З поняття рівності між числами випливає більш широке поняття відношення еквівалентності на множинах. За аналогією деякі нерівності також можуть бути використані як моделі для більш широкого класу відношень.Означення. Відношення називається відношенням нестрогого порядку, якщо воно рефлексивне, антисиметричне і транзитивне.Відношення нестрогого порядку є узагальненням відношення на множині натуральних чисел, тому можна легко перевірити властивості цього відношення:1) рефлексивність: 2) антисиметричність:;3) транзитивність: Означення. Відношення називається відношенням строгого порядку, якщо воно антирефлексивне, асиметричне і транзитивне.Відношення строгого порядку є узагальненням відношення на множині натуральних чисел, тому можна легко перевірити властивості цього відношення: 1) антирефлексивність: 2) асиметричність:;3) транзитивність: Обидва типи відношень називаються відношенням порядку.Означення. Множина, на якій задане відношення порядку, називається цілком впорядкованою, якщо будь-які два елементи з знаходяться в цьому відношенні і частково впорядкованою в противному випадку.Означення. Відношення порядку називається відношенням лінійного порядку, якщо додатково виконується властивість: (для нестрогого порядку) або (для строгого порядку).Означення. Множина, на якій задане відношення лінійного порядку, називається лінійно впорядкованою.Приклади:1. і – відношення нестрогого порядку для чисел; і – відношення строгого порядку. Обидва відношення цілком впорядковують множини і.. На множині підмножин множини відношення нестрогого включення задає нестрогий частковий порядок, а відношення строгого включення задає строгий частковий порядок. Перевіримо властивості відношення нестрогого включення:1) рефлексивність:;2) антисимметричність:;3) транзитивність:.Означення. Відношення називається відношенням домінування, якщо воно антирефлексивне, асиметричне і для нього може не виконуватися властивість транзитивності.Означення. Відношення називається відношенням толерантності, якщо воно рефлексивне, симетричне, але не транзитивне.

16. Поняття відповідності. Відповідність обернена даній
Відповідністю між множинами A і B в теорії множин називається будь-яка підмножина C декартового добутку A?B. Якщо (a, b)?C, то кажуть, що елемент b відповідає елементу a при відповідності C.Обернена відповідністьВідповідністю, оберненою до заданої відповідності C між множинами A і B, називається відповідність D між множинами B і A така, що D ={(b, a) | (a, b)?C}.Відповідність, обернену до відповідності C, позначають C-1.Обернена відповідністьВідповідністю, оберненою до заданої відповідності C між множинами A і B, називається відповідність D між множинами B і A така, що D ={(b, a) | (a, b)?C}.Відповідність, обернену до відповідності C, позначають C-1.Композиція відповідностейЯкщо задано відповідності і, то композицією відповідностей і (позначається) називається відповідність між множинами і така, щоВідповідності, функції та відображенняУ математичній літературі прийнято називати відповідність C?A?B функціональною відповідністю або функцією з A в B, якщо кожному елементові a?Pr1 C відповідає тільки один елемент з Pr2 C.Термін відображення зазвичай вживається як синонім функції, але деякі джерела схильні розрізняти ці поняття, причому в одних функцією називається таке відображення, яке є всюди визначеним, а в інших — навпаки: відображенням вважається така функція, яка є всюди визначеною.

17. Взаємнооднозначні відповідності. Рівнопотужні площини. Приклади.
Взаємне однозначна відповідність (математичне), така відповідність між елементами двох безлічі, при якому кожному елементу першої безлічі відповідає один певний елемент другої безлічі, а кожному елементу другої безлічі — один певний елемент першої безлічі. Ст о. с. — приватний вигляд функції або відображення, коли дана функція і їй зворотна є однозначними. Якщо між двома безліччю можна встановити Ст о. с., то ця безліч називається еквівалентною, або рівнопотужними. Наприклад, безлічі цілих і їх квадратів равномощни, оскільки відповідність n ® n 2 є Ст о. с.

18. Натуральні числа та їх властивості. Число нуль. Множина цілих невід’ємних чисел. Порядкові і кількісні натуральні числа. Лічба.
Натура?льні чи?сла — числа, що виникають природним чином при лічбі. Це числа: 1, 2, 3, 4, … Множину натуральних чисел прийнято позначати знаком Існують два основних підходи до означення натуральних чисел:числа, що використовуються при лічбі предметів (перший, другий, третій…) — підхід, загальноприйнятий у більшості країн світу; формалізованим різновидом цього підходу є аксіоматичне описання системи натуральних чисел за допомогою аксіом Пеано.числа для позначення кількості предметів (відсутність предметів, один предмет, два предмети…) — підхід, прийнятий у роботах Ніколя Бурбакі, де натуральне число означається як потужність скінченних множин; при такому підході, як правило, 0 відносять до натуральних чисел.Від'ємні та дробові числа не є натуральними числами.Множина натуральних чисел є нескінченною: для будь-якого натурального числа знайдеться інше натуральне число, більше за нього.Властивості:1.Комутативність додавання:a+b=b+a2.Комутативність множення:ab=ba3.Асоціативність додавання:(a+b)+c=a+(b+c)4.Асоціативність множення: (ab)c=a(bc) 0 — цифра й одночасно число, нейтральний елемент для операції додавання. Множення будь-якого елемента множини на нуль дає нуль.Існує два підходи до визначення натуральних чисел, що відрізняються належністю нуля множині натуральних чисел. В радянській школі прийнято не відносити нуль до натуральних чисел.Будь-яке число в нульовому степені буде дорівнювати одиниці.Властивості множини цілих невід’ємних чисел1. Множина цілих невід’ємних чисел впорядкована. Наприклад, вона впорядковується відношенням «менше», яке є транзитивним і антисиметричним.Для будь — яких цілих невід’ємних чисел а і b може виконуватись одне з трьох відношень: а b, а = b, а b.Можна розташувати числа так, щоб для будь-яких двох чисел спочатку йшло число менше, тоді отримаємо ряд цілих невід’ємних чисел: 0,1, 2, З, 4,…2. Множина цілих невід’ємних чисел нескінченна. Для кожного цілого невід’ємного числа а можна вказати число, яке слідує безпосередньо за ним. Це число а + 1.3. Множина цілих невід’ємних чисел дискретна. Це означає, що не можна вказати таке натуральне число, яке знаходиться між цілими невід’ємних числами а і а + 1. Самі ці числа називаються сусідніми.

20.Додавання цілих невід’ємних чисел. Теорема про існування і єдиність суми.
Сумою цілих невід’ємних чисел а і б називають число елементів в об'єднанні непересічних множин. А+b=n(AύB),де n(A)=a,b I A∩B =ᴓСума декількох доданків:нехай сума двох доданків визначена і визначена сума n доданків.Тоді сума складається з n+1 доданка,сума а1+а2+…аn+an +1,дорівнює (а1+а2+…+an)+an +1.

21.Закони додавання на множині цілих невід’ємних чисел
Закон-:для будь-яких цілих невід'ємних чисел а і б виконується рівність а + б = б + аНехай а-число елементів в множині А,b-число елементів в множині В і А∩В=ᴓ.Тоді з визначення суми цілих невід’ємних чисел а + б є число елементів об’єднання множин А і В: а+b = n (AυB).Але множина Аυдорівнює множині ВυА згідно змістовній властивості об’єднання множин і значить n (AυB)=n(BυA).По визначенню суми n(BυA)=b+a тому a+b=b+a для будь-яких цілих невід’ємних чисел а і б.Докажемо тепер сполучний закон,докажемо,що для будь-яких цілих невід’ємних чисел а,b,c виконується рівність (a+b)+c=a+(b+c). Нехай а=n(A) b=n(B) c=n(C) причому A∩B=ᴓ B∩C=ᴓ.Тоді по визначенню суми двох чисел можна записати (а+b)+c=n(AυB)+n(C)=n(AυB)υC).Так як об'єднання множин підчиняється сполучному закону,то n((AυB)υC)=n(Aυ(BυC)).Звідси по визначенню суми двох чисел маємо n(Aυ(BυC__=n(A)+n(BυC)=a+(b+c). Отже, (a+b)+c = a+(b+c) для будь-яких цілих невід’ємних чисел a, b,c.

22. Відношення «дорівнює» і «менше» на множині цілих невід’ємних чисел:а) виходячи з теоретико – множинних позоцій;б) через суму;в) через відрізок чисел натурального ряду.
Нехай дано два цілих невід’ємних числа а і б.З теоретико-множинної точки зору вони являють собою число елементів кінцевих множин А іВ:а=n(A) b=n(B).Якщо ці множини рівно потужні то їм відповідає одне і те ж число а=б.Приходимо до визначення: числа а і б рівні якщо вони визначаються рівно потужними множинами: a=b↔A≈B деn(A)=a n(B)=b.Якщо множина А і В нерівно потужна,то числа,визначувані ними різні.В такому випадку,якщо множина А рівно потужна власній підмножині безлічі В і n(A)=a n(B) =b,говорять,що число а менше числа б и пишуть:a˂b.В такій ситуації говорять,що b більше а і пишуть: b˃а a.˂b↔A≈B1∩B і B1≠B B1≠ᴓ.Друге визначення відношення «менше»:
Число а менше числа b тоді і тільки тоді коли існує таке натуральне число с,що а+с=b.Таким чином виходить ще одне визначення відношення «менше»: число а менше числа b тоді і тільки тоді коли відрізок натурального ряду Na є власною підмножиною відрізка цього ряду Nb: a˂b↔NaυNb I Na ≠Nb/

23. Означення віднімання через теоретико-множинний зміст.Означення віднімання через суму
Вираз:Різницею цілих невід'ємних чисел а і b назіваеться число елементів в доповненні множини В до безлічі А при умові що n(A)=a n(B)=b I B∩A
a-b=n(A/B) де a=n(A) b=n(B) B∩A.Визначення:Різницею цілих невід’ємних чисел а і b називають таке ціле невід’ємне число с сума чкого і числа b рівна а. a-b=c↔a=b+c

24 Теорема про існування і єдиність різниці.
Теорема: Різниця цілих невід’ємних чисел а і b існує тоді і тільки тоді коли b≤a/Доказ:Якщо а=b то а-b=0 і звідси рівність а-bіснує.Якщо b більше а то по визначенню відношення «менше» існує таке натуральне число с,що а=b+с.Тоді по визначенню рівності с=а-b різниця а-b існує.Якщо рівність а-b існує,то по визначенню різниці знайдеться таке ціле невід’ємне число с,що а=b+с.Якщо с=0,то а=b;якщо с більше за 0,то bменше за а по визначенню «менше».Значить b≤а.
Теорема:Якщо різниця цілих невід’ємних чисел а і b існує,то вона єдина.Доказ:Уявімо,що існує два значення різниці а-b:а-b=с1 і а-b=с2.Тоді по визначенню різниці маємо а=b+c1 I a=b+c2.Звідси береться b+c1=b+c2 і значить с1=с2.

25.Правила віднімання числа від суми.
Щоб відняти число від суми, достатньо відняти його з одного з доданків і до отриманого результату додати інший доданок: а) якщо, то, б) якщо, то.Щоб відняти від числа суму чисел, достатньо відняти від цього числа послідовно доданки.

26. Правила віднімання суми від числа.
Щоб відняти суму від числа потрібно відняти віз цього числа послідовно кожний доданок один за другим,якщо a,b,c-цілі невід’ємні числа,то при а≥b+с маємо a-(b+c)=(a-b)-c.

30. Ділення цілих невід’ємних чисел. Означення ділення через теоретико-множинний зміст та через добуток.
Розглянемо приклад 8:2 = 4.Проаналізуймо його.У прикладі розглядається множина, в якій 8 елементів. Вона розбивається на підмножини, в кожній з яких по 2 елементи, тобто на рівнопотужні підмножини.Більше того,вони попарно не перетинаються.Таким чином число 4 отримане в відповіді-це число двохелементних підмножин,на які розбита множина з 8 елементів.Приватним цілого невід'ємне числа а і натурального числа b називається таке ціле невід'ємне число c=a:b, «произвидение» якого і числа b дорівнює a.

32.Теорема про неможливість ділення на нуль.
Проблема полягає не у складності здійснення операції, а у неможливості в принципі за обмежень сучасної теорії чисел. Фактично, в якій галузі математики ми б не розвивали заборони чи невідомості, знову стикаємось з діленням на нуль: там ї≠0, там "проходить якомога близько, але не перетинається"... школоті взагалі пояснюють з 1-ого(чи коли починають вчити математику): на нуль ділити не можна. Ура! Тоді ніяких проблем. Насправді причина в тому, що за здійснення операції створюється кілька парадоксів, допущення яких як наслідок допущення операції зруйнує всю алгебру.Сформулюємо правило: При ділення нуля на будь-яке число в частці дістаємо нуль. 0: а =0 Про неможливість ділення на нуль слід повідомити так: ділити на нуль не можна. Наприклад, не можна 7 поділити на 0, бо немає такого числа, при множенні якого на 0 дістали б 7.Можуть виявитися учні, яких зацікавлять питання – чому? Вчитель повинен бути готовий до такого питання.Якщо а: 0 =х х = 0 х? 0 а: 0 = 0 а: 0 = х 0 · 0 = а х · 0 = а а = 0 Маємо протиріччя а = 0

33. Правила ділення суми на число
Щоб поділити суму на число, достатньо поділити кожний доданок на це число і додати здобуті частки.(6 + 4): 2 = 6: 2 + 4: 2 = 3 + 2 = 5. (а + в): с = а: с + в: с

34 Правила ділення різниці на число..
Щоб поділити різницю чисел на дане число, достатньо поділити на це число зменшуване і від'ємник.Потім від першої частки відняти другу.(80 - 24): 4 = 80: 4 - 24: 4 = 20 - 6 = 14 (а - в): с = а: с - в: с

36. Правило ділення числа на добуток та множення числа на частку.
Щоб поділити число на добуток двох чисел, достатньо подлити це число на один із множників, а потім результат поділити на другий множник. 12: (2 х 3) = 12: 2: 3 = 6: 3 = 2 а: (в х с) = (а: в): с = (а: с): в

37. Ділення з остачею.
Виконати ділення з остачею - знайти найбільше ціле число, яке у добутку з дільником дає число, що не перевищує ділене. Це число називається неповною часткою. Різниця між діленим і добутком дільника на неповну частку називається остачею.19: 3 =... (ост. 1) 18 і 1

19: 3 = 6 (ост. 1) ділене дільник частка остача

38. Позиційна і непозиційна система числення. Запис чисел в десятковій системі числення. Запис чисел в різних позиційних системах числення, відмінних від десяткової.
Загальновживана форма запису числа є насправді не що інше, як скорочена форма запису розкладу за степенями основи системи числення, наприклад

130678=1*105+3*104+0*103+6*102+7*101+8

1. Для переведення чисел із системи числення з основою p в систему числення з основою q, використовуючи арифметику нової системи числення з основою q, потрібно записати коефіцієнти розкладу, основи степенів і показники степенів у системі з основою q і виконати всі дії в цій самій системі. Очевидно, що це правило зручне при переведенні до десяткової системи числення. Наприклад: з вісімкової в десяткову:

7358=7*1082+3*1081+5*1080= 7*8102+3*8101+5*8100=47710

Алгоритм Евкліда.

Найбільший спільний дільник двох чисел це найбільше число, що ділить обидва дані числа без залишку. Алгоритм Евкліда оснований на тому, що НСД не змінюється, якщо від більшого числа відняти менше. Наприклад, 21 є НСД чисел 252 та 105 (252 = 21 × 12; 105 = 21 × 5); оскільки 252 − 105 = 147, НСД 147 та 105 також 21. Оскільки більше з двох чисел постійно зменшується, повторне виконання цього кроку дає все менші числа, поки одне з них не дорівнюватиме нулю. Коли одне з чисел дорівнюватиме нулю, те, що залишилось, і є НСД. Обертаючи кроки алгоритму Евкліда у зворотний порядок, НСД можна виразити як лінійну комбінацію даних чисел помножених на цілі коефіцієнти, наприклад 21 = 5 × 105 + (−2) × 252

Характеристики:

Алгоритм

Алгоритм Евкліда ітеративний, тобто, пошук розв'язку відбувається за декілька кроків. Для того щоб знайти НСД(a, b) на 0-му кроці знаходять остачу r ₀ від ділення a на b. На 1-му кроці знаходять остачу від ділення b на r ₀. Оскільки залишки зменшуються на кожному кроці але не можуть бути від'ємними, то цю операцію виконують n кроків до тих пір поки не отримують остачу 0. Найбільшим спільним дільником є остання не нульова остача r_{n −1}. Кількість кроків в алгоритмі має бути скінченною, оскільки існує лише скінченна кількість цілих чисел між початковим залишком r ₀ та нулем.

 

Класифікація – це дія розподілу об’єктів по класах на основі схожості об’єктів інших об’єктів. Множина х розбита на класи, якщо: 1. підмножина попарно не перетинається 2. об’єднання підмножин утворює множину х Якщо не виконується хоча б одна з цих вимог, класифікація вважається неправильною. Так, множина Х трикутників можна розбити на 3 класи: гострокутні, прямокутні, тупокутні. Вірно, виділені підмножини попарно не перетинаються(серед гострокутних немає тупокутних і прямокутних, серед прямокутних немає гострокутних і тупокутних тощо) і їх об’єднання співпадає з множиною Х. Проте не кожна система підмножин даної множини являє собою розбиття цієї множини. Наприклад, якщо з множини Х трикутників виділити підмножини рівнобедрених,рівносторонніх і різносторонніх, то розбиття множини Х на класи ми не отримаємо, оскільки множина рівнобедрених, і рівносторонніх трикутників перетинаються (всі ріностороні трикутники являються рівнобедреними). Для того щоб виділити підмножину достатньо вказати характеристичні властивості його елементів.

Розглянемо, наприклад, множину натуральних чисел. Його елементи володіють різними властивостями. Серед натуральних чисел є парні, непарні, кратні 3, кратні 5 тощо. Припустимо, що нас цікавлять числа, що володіють властивістю ділитися на 3. ця властивість дозволяє виділити з множини натуральних чисел підмножину чисел, кратних 3. тоді про інші числа ми можемо сказати, що вони не кратні 3, отже отримуємо ще одну підмножину множини натуральних чисел. Виділені підмножини не перетинаються, а їх об’єднання співпадає з множиною натуральних чисел. Таким чином, задання одних властивостей елементів множини натуральних чисел привело до розбиття цієї множини на 2 класа: клас чисел, кратних 3 (3,6,15), і клас чисел, не кратних 3 (2,4,5,7). А яким буде розбиття на класи, якщо вказати 2 властивості, тобто виділити з множини 2 різні підмножини? Розглянемо 2 властивості натуральних чисел: «бути кратним 3» і «бути кратним 5». За допомогою цих властивостей із множини натуральних чисел можна виділити 2 підмножини: А – підмножина чисел кратних 3, В – підмножина чисел кратних 5. ці підмножини перетинаються, але ні одне з них не являється підмножиною іншого. Проаналізуємо те, що вийшло. Круг, що зображає множину натуральних чисел, розбився на 4 області, що перетинаються – вони пронумеровані. Кожна область зображає деякі підмножини множини натуральних чисел. Підмножина 1 складається з чисел кратних 3,5. підмножина 2 – кратних 3, і не кратних 5. підмножина 3 – кратних 5 і не кратних 3. підмножина 4 – числа, що не кратні ні 3, ні 5. поєднує ці 4 підмножини множина натуральних чисел. Таким чином, виділення 2 властивостей натуральних чисел призвело до розбиття множини на 4 класи. Але так буває не завжди.

10.Декартів добуток. Кортеж. Число елементів декартового добутку.

Декартовим добутком множин А і В називається множина, елементами якої є всі упорядковані пари (а, b) такі, що перший компонент яких єналежить множині А, а другий компонент належить множині В.

Позначається декартів добуток А×В (але не А∙В або АВ).

Нехай А ={a1, a2, a3} i B = {b1, b2}. Знайдемо А×В і В×А.

А×В = {(a1, b1), (a1, b2), (a2, b1), (a2, b2),(a3, b1), (a3, b2)},

B×A = {(b1, a1), (b1, a2), (b1, a3), (b2, a1), (b2, a2), (b2, a3)}.

Із означення видно, що декартів добуток не має переставної властивості: А×В ≠ В×А

Переставна властивість декартового добутку двох різних множин має місце лише тоді, коли одна з них порожня: А×Ø = Ø×А = Ø

Декартів добуток двох рівних множин називають декартовим квадратом: А×А = А2, трьох множин – декартовим кубом і т. д.

Декартів добуток множин не підчинається і сполучному закону, але пов'язаний з операцією об’єднання множин розподільною властивістю: для будь – яких множин А, В і С маємо рівність

Елементи декартового добутку 2 кінчених множин краще записувати за допомогою таблиці. Наприклад. А= (1,2,3) В = (3,5)

А/В

(1,3)

(1,5)

(2,3)

(2,5)

(3,3)

(3,5)

В математиці розглядають не тільки упорядковані пари, а й упорядковані набори з 3, 4 і тощо елементів. Такі набори ще називають кортежами. Так (1,2,3) – кортеж довжиною 3 (так як в ньому 3 елементи), а (7,6,5,4,9) – кортеж довжиною 5.