
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения и функции – математический аппарат изучения явлений в физикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математика – наука прикладная. Функции прямой и обратной пропорциональностей можно почти одновременно изучить как на уроках алгебры, так и на уроках физики в 7-8 классах. При изучении данных тем необходимо еще раз обратить внимание учащихся на то, что с увеличением аргумента значение функции обратной пропорциональности уменьшается. Рассмотрим применение прямой и обратной пропорциональности на уроках физики на примере темы «Закон Ома для участка цепи». Различные действия тока, такие, как нагревание проводника, магнитные и химические действия, зависят от силы тока. Изменяя силу тока в цепи, можно регулировать эти действия. Но, чтобы управлять током в цепи, надо знать, от чего зависит сила тока в ней. Ученикам нужно объяснить, что электрический ток в цепи - это упорядоченное движение заряженных частиц в электрическом поле. Чем сильнее действие электрического поля на эти частицы, тем больше сила тока в цепи. Но действие поля характеризуется физической величиной - напряжением. Поэтому можно предположить, что сила тока зависит от напряжения. Установим, какова эта зависимость, на опыте.
Собираем электрическую цепь, состоящую из источника тока, амперметра, спирали из никелиновой проволоки, ключа и параллельно присоединенного к спирали вольтметра. Замыкаем цепь и отмечаем показания приборов. Затем присоединяем к первому аккумулятору второй такой же аккумулятор и снова замыкаем цепь. Напряжение на спирали при этом увеличится вдвое, и амперметр покажет вдвое большую силу тока. При трех аккумуляторах напряжение на спирали увеличивается втрое, во столько, же раз увеличивается сила тока. Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нем. Другими словами, сила тока в проводнике прямо пропорциональна напряжению на концах проводника. Составим график зависимости силы тока в проводнике от напряжения между концами этого проводника. На графике в условно выбранном масштабе по горизонтальной оси отложено напряжение в вольтах, а по вертикальной - сила тока в амперах. Видим, что зависимость напряжения от силы тока прямо пропорциональна. Прямолинейное равномерное движение можно описать при помощи графика линейной функции. Рассмотрим задачу, которую можно предложить семиклассникам при изучении линейных функций на уроках алгебры. Задача. Пешеход движется равномерно со скоростью 4 км/ч из пункта А в пункт В. Задайте формулой зависимость расстояния S, пройденного пешеходом от времени t. Решение: S = 4t
Задача. Автобус и мотоциклист движутся навстречу друг другу со скоростями 10м/с и 20 м/с. Расстояние между ними в момент начала наблюдения равно 500 м. Считая, что ось Х направления в сторону движения автобуса и при t=0 положение автобуса совпадает с началом отсчета, написать для автобуса и мотоциклиста уравнения х=х(t). Решение.
Формулу силы тяжести F=mg, можно получить, выполнив на уроке эксперимент и построив график зависимости F(m).
Знания линейных функций будут необходимы при выполнении лабораторной работы «Изучение зависимости силы упругости от деформации тела» для более наглядного представления прямо пропорциональной зависимости между физическими величинами. Для проведения работы понадобятся пружина и 4 грузика по 102 грамма. 1. Измерим длину нерастянутой пружины. 2. Подвесим один грузик массой 0,1 кг к пружине и снова измерим длину пружины. 3. Подвесим второй грузик, теперь масса груза на пружине составляет массой 0,2 кг, измерим длину пружины. 4. Подвесим третий грузик и измерим длину пружины, которая растянулась под действием груза массой 0,3 кг 5. Подвесим еще грузик и получим груз массой 0,4 кг, подвешенный на пружине; измерим длину пружины Построим график зависимости F от l. На координатной плоскости отметим точки… Соединим получившиеся точки… Графиком данной зависимости является - прямая. Мы знаем, что кроме силы тяжести направленной вертикально вниз на тело действует и сила упругости, направленная вертикально вверх в нашем случае сила тяжести грузов, подвешенных к пружине, уравновешивается силой упругости, возникшей в пружине.
Линейные функции можно использовать при изучении темы «Плотность». Задача. Записать формулу зависимости массы стальной балки от её объема, если V – объем балки, m - его масса, плотность стали 7,8. Построить график этой зависимости. Решение: m=ρV; ρ=7,8; m =7,8V; у=k·х;
Многие реальные ситуации моделируют с помощью прямой пропорциональности. Например, Рассмотрим уравнение S=2t. Если принять, что это формула расстояния: S= V t, то можно предложить построить график этого уравнения и найти по графику путь, пройденный за 4 секунды?
По уравнению у = 0,5х + 4 можно описать движение. Здесь движущееся тело находится на расстоянии 4 метров от наблюдателя спереди и отдаляется от него со скоростью 0,5 м/с. Можно также построить график и провести анализ. При изучении на уроках алгебры линейных и квадратных уравнений учителю желательно использовать физические задачи, что позволит впоследствии применять полученные знания на уроках физики. Для этого необходимо показать различие и сходство при решении задачи математическим и физическим способами. Решим следующую задачу. В лесу мимо пня, на котором сидела Маша, в 10 часов 00 минут пробежал Медведь со скоростью 0,9 км/ч. Через некоторое время в 10 часов 06 минут Маша пустилась в погоню за Медведем со скоростью 1,8 км/ч. Сколько времени понадобится Маше, чтобы догнать Медведя? Рассмотрим математический способ решения: - Для решения данной задачи нам понадобится таблица.
Определим: - Какая физическая величина известна? - Какой путь S, пробежал каждый? - Что можно сказать о времени t? (время движения Маши на 6 мин меньше) - Как можно выразить 6 мин в часах? - Какое время возьмем за х? (наименьшее – время движения Маши) - Тогда какое время был в пути Медведь? (на 0,1 ч больше, т.е. х+0,1 ч) Заполним таблицу. Нам известна скорость объектов, известно, что путь, который пробежали Маша и Медведь, одинаков. Время движения Маши на 6 минут меньше, чем у Медведя. Выразим 6 мин в часах. Пусть х – время движения Маши, тогда время движения Медведя х+1. Определим расстояние, которое пробежала Маша: S1 = 1,8 х. Определим расстояние, которое пробежал Медведь: S2 = 0,9(х+0,1). Т.к. S1= S2, то 1,8х =0,9(х+0,1). Решим данное равенство и найдем х. х=0,1 часа.
1,8х =0,9(х+0,1) 1,8х –0,9 х – 0,09 = 0 0,9х – 0,09 = 0 0,9х = 0,09 х = 0,09/0,9 х = 0,1 часа – время Маши Ответ: Время Маши – 0,1 часа. Запишем физический способ решения задачи.
Учащимся можно предложить составить задачу по рисунку и решить её математическим и физическим способами, 
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.007 с.) |





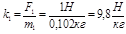



 .
g- ускорение свободного падения
.
g- ускорение свободного падения




 Решение:
Решение:




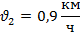

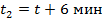





 , т.к.
, т.к. 
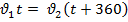



 Ответ:
Ответ: 
 -?
-?



