
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математический способ решенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Составляем уравнение 4х + 2х = 54 6х = 54 х = 2х = 2∙9 = 18 км/ч Ответ: Через 2 часа скорость первого равна 18 км/ч и скорость второго - 9 км/ч. Физический способ решения.
используя алгоритм:
Линейные функции применяются во многих физических процессах: - в кинематике – это графики пути, перемещения, координаты прямолинейного равномерного движения; скорости, ускорения при прямолинейном равнопеременном движении; - в динамике - графики зависимости Fтяж (m), Fтр (P), Fупр (x),… - в разделе «законы сохранения» - графики зависимостей Еп(h), W(t), p (t),… - в квантовой физике - графики Екин (частота падающего света) в теории фотоэффекта. В 8 классе ученики учатся решать дробные уравнения. Для чего нужны дробные уравнения? Какие задачи приводят к их появлению? В физике это задачи, в которых одна величина выражается через другие при помощи дробного выражения (содержащего переменную в знаменателе дроби). Например: время = сторона прямоугольника = цена = производительность =
В приложении 1 к данной части можно ознакомиться с решением математических задач, которые актуальны и на уроках физики.
Применение векторного анализа и теоремы Пифагора При решении задач по физике Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию направление, смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков. На уроках физики учитель дает определение радиус-вектора при изучении механических явлений. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например, скорость, перемещение, импульс, напряженность электрического поля, сила. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов также используют на уроках физики неоднократно, изучая разные темы в разных классах. Интуитивное понимание вектора у учащихся складывается с первых же уроков физики в 7 и 8 классе. Проведем сравнение понятия вектора в физике и математике:
Понимание вектора в физике и математике происходит поэтапно, когда ученики раскрывают и изучают следующие вопросы: В математике: · Координатная прямая. · Координатная плоскость. · Координаты точки. В физике: · Понятие системы отсчета. · Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество. Понятие вектор и нулевой вектор, в каком случае проекция вектора на ось считается положительной, отрицательной, равной нулю, - рассматривается как в математике, так и в физике. Координаты вектора в физике рассматриваем относительно перемещения тела. Интеграцию обоих предметов необходимо осуществлять при изучении сложения векторов. В математике это правило треугольника, параллелограмма, многоугольника, произведение векторов. В физике прикладной характер правил сложения векторов виден не при определении перемещения тела, а при сложении скоростей движущегося тела, при вычислении механической работы.
Глубокое понимание вектора и действий с векторами у учеников сложится только посредством интеграции математического и физического определения этих понятий. Рассмотрим пример задачи, при решении которой применяется теорема Пифагора.
На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота? Решение: По теореме Пифагора На уроках физики ученики сталкиваются с теоремой Пифагора чаще всего при изучении механических и оптических явлений. В приложении к данному выступлению можно ознакомиться с подборкой задач на применение векторного анализа и правила треугольника (Приложение 3).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

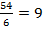 км/ч
км/ч









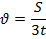

 Ответ:через 2 часа скорость первого равна 5 м/с и скорость второго – 2,5 м/с.
Ответ:через 2 часа скорость первого равна 5 м/с и скорость второго – 2,5 м/с.
 -?
-?

 , скорость =
, скорость =  ;
;
 количество =
количество = 
 время =
время =  .
.
 Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy).
Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy).

 Правило параллелограмма.
Правило параллелограмма.
 Правило многоугольника.
Правило многоугольника.

 . Соответствующий многоугольник (треугольник) перемещений выглядит таким образом:
. Соответствующий многоугольник (треугольник) перемещений выглядит таким образом: 

 , то выражение для скорости в любой момент t времени имеет вид:
, то выражение для скорости в любой момент t времени имеет вид:  .
.



 Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела.
Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела.

 Произведение векторов – скалярная величина.
Произведение векторов – скалярная величина.
 Механическая работа – скалярная величина.
Механическая работа – скалярная величина.
 Задача индийского математика XII века Бхаскары.
Задача индийского математика XII века Бхаскары. . Высота тополя равна
. Высота тополя равна  м.
м.


