
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Концепция интегрированного обученияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Часть 1. Принципы интегрированного обучения. · Синтезированность знаний. Целостное, синтезированное, систематизированное восприятие изучаемых по той или иной теме вопросов способствует развитию широты мышления. Постановка проблемы, исследуемой методами интеграции, развивает целенаправленность и активность мышления. · Углублённость изучения. Более глубокое проникновение в суть изучаемой темы способствует развитию глубины мышления. · Актуальность или практическая значимость проблемы. Обязательная реализация рассматриваемой проблемы в какой-то практической ситуации усиливает практическую направленность обучения, что развивает критичность мышления, способность сопоставлять теорию с практикой. · Альтернативность решения. Новые подходы к известной ситуации, нестандартные способы решения проблемы, возможность выбора решения данной проблемы способствуют развитию гибкости мышления, развивают оригинальность мышления. Сопоставление решений развивает активность, критичность, организованность мышления. За счёт стремления осуществлять разумный выбор действий, отыскивать наиболее краткий путь достижения цели развивается целенаправленность, рациональность, экономия мышления. · Доказательность решения. Доказательность решения проблемы развивает доказательность мышления. Интеграция — необходимое условие современного учебного процесса, её возможная реализация в рамках какой-либо школы была бы переходом этой школы на новый качественный уровень образования. Основной задачей образования на современном этапе является формирование конкурентоспособной личности, подготовка выпускника школы такого уровня, чтобы, попадая в проблемную ситуацию, он мог найти несколько способов ее решения, выбрать рациональный способ, обосновать свое решение. Компетентностный подход сменил целевые ориентиры: от знающего ученика - к умелому, от обученного - к умеющему учиться. Мы говорили о том, что в подготовке и проведении интегрированного урока участвует несколько учителей. Но стоит отметить, что такие уроки может проводить и один учитель, владеющий материалом интегрируемой дисциплины. Такие ситуации становятся сегодня нормой. Преимущества многопредметного интегрированного урока перед традиционным монопредметным очевидны. На таком уроке можно создать более благоприятные условия для развития самых разных интеллектуальных умений учащихся, через него можно выйти на формирование более широкого синергетического мышления, научить применению теоретических знаний в практической жизни, в конкретных жизненных, профессиональных и научных ситуациях. Интегрированные уроки приближают процесс обучения к жизни, натурализируют его, оживляют духом времени, наполняют смыслом. Чтобы научить детей думать, открывать, изобретать, учитель должен самосовершенствоваться.
Часть 2. Активизация познавательной деятельности обучающихся посредством интеграции предметов на примере математики и физики Необходимость обращения к интегрированному обучению вызвана рядом проблем, с которыми приходится сталкиваться учителям-предметникам при реализации образовательной программы в основной и старшей школе. Заметное снижение интереса у учащихся к предметам естественно-математического цикла, которое обусловлено сложностью программного материала по физике и математике. Сама специфика предметов естественно-математического цикла побуждает к комплексному подходу в обучении школьников, т.е. логика данных наук ведёт к их интеграции, взаимопроникновению, объединению отдельных тем. Несогласованность программ по изучаемым в школе предметам естественно-математического цикла приводит к тому, что одна и та же тема по физике и математике изучается в разное время. Эти противоречия легко снимаются в интегрированном обучении, которое позволяет решить ещё одну проблему — временную, т.е. межпредметная интеграция позволяет учителю экономить учебное время. Чтобы научить детей думать, открывать, изобретать, учитель должен самосовершенствоваться. Огонь знаний в глазах учеников зажигается только при условии активной творческой деятельности педагога. Учителя математики и физики, преподавая свой предмет, совсем не учитывают того, что некоторые вопросы нужно сначала изучить на уроках математики, а затем применять на уроках физики. Ещё хуже, когда математик во время объяснения новой темы совсем не говорит о её применении в физике. Современный курс математики построен на идеях множества, функции геометрических преобразований, охватывающих различные виды симметрии. Школьники изучают производные элементарных функций, интегралы и дифференциальные уравнения. Математика не только дает физике вычислительный аппарат, но и обогащает её в идейном плане. На уроках математики школьники учатся работать с математическими выражениями, а задача преподавания физики состоит в том, чтобы познакомить учащихся с переходом от математических явлений к физическим и связей между ними.
Решение.
Формулу силы тяжести F=mg, можно получить, выполнив на уроке эксперимент и построив график зависимости F(m).
Знания линейных функций будут необходимы при выполнении лабораторной работы «Изучение зависимости силы упругости от деформации тела» для более наглядного представления прямо пропорциональной зависимости между физическими величинами. Для проведения работы понадобятся пружина и 4 грузика по 102 грамма. 1. Измерим длину нерастянутой пружины. 2. Подвесим один грузик массой 0,1 кг к пружине и снова измерим длину пружины. 3. Подвесим второй грузик, теперь масса груза на пружине составляет массой 0,2 кг, измерим длину пружины. 4. Подвесим третий грузик и измерим длину пружины, которая растянулась под действием груза массой 0,3 кг 5. Подвесим еще грузик и получим груз массой 0,4 кг, подвешенный на пружине; измерим длину пружины Построим график зависимости F от l. На координатной плоскости отметим точки… Соединим получившиеся точки… Графиком данной зависимости является - прямая. Мы знаем, что кроме силы тяжести направленной вертикально вниз на тело действует и сила упругости, направленная вертикально вверх в нашем случае сила тяжести грузов, подвешенных к пружине, уравновешивается силой упругости, возникшей в пружине.
Линейные функции можно использовать при изучении темы «Плотность». Задача. Записать формулу зависимости массы стальной балки от её объема, если V – объем балки, m - его масса, плотность стали 7,8. Построить график этой зависимости. Решение: m=ρV; ρ=7,8; m =7,8V; у=k·х;
Многие реальные ситуации моделируют с помощью прямой пропорциональности. Например, Рассмотрим уравнение S=2t. Если принять, что это формула расстояния: S= V t, то можно предложить построить график этого уравнения и найти по графику путь, пройденный за 4 секунды?
По уравнению у = 0,5х + 4 можно описать движение. Здесь движущееся тело находится на расстоянии 4 метров от наблюдателя спереди и отдаляется от него со скоростью 0,5 м/с. Можно также построить график и провести анализ. При изучении на уроках алгебры линейных и квадратных уравнений учителю желательно использовать физические задачи, что позволит впоследствии применять полученные знания на уроках физики. Для этого необходимо показать различие и сходство при решении задачи математическим и физическим способами. Решим следующую задачу. В лесу мимо пня, на котором сидела Маша, в 10 часов 00 минут пробежал Медведь со скоростью 0,9 км/ч. Через некоторое время в 10 часов 06 минут Маша пустилась в погоню за Медведем со скоростью 1,8 км/ч. Сколько времени понадобится Маше, чтобы догнать Медведя? Рассмотрим математический способ решения: - Для решения данной задачи нам понадобится таблица.
Определим: - Какая физическая величина известна? - Какой путь S, пробежал каждый? - Что можно сказать о времени t? (время движения Маши на 6 мин меньше) - Как можно выразить 6 мин в часах? - Какое время возьмем за х? (наименьшее – время движения Маши) - Тогда какое время был в пути Медведь? (на 0,1 ч больше, т.е. х+0,1 ч) Заполним таблицу. Нам известна скорость объектов, известно, что путь, который пробежали Маша и Медведь, одинаков. Время движения Маши на 6 минут меньше, чем у Медведя. Выразим 6 мин в часах. Пусть х – время движения Маши, тогда время движения Медведя х+1. Определим расстояние, которое пробежала Маша: S1 = 1,8 х. Определим расстояние, которое пробежал Медведь: S2 = 0,9(х+0,1). Т.к. S1= S2, то 1,8х =0,9(х+0,1). Решим данное равенство и найдем х. х=0,1 часа.
1,8х =0,9(х+0,1) 1,8х –0,9 х – 0,09 = 0 0,9х – 0,09 = 0 0,9х = 0,09 х = 0,09/0,9 х = 0,1 часа – время Маши Ответ: Время Маши – 0,1 часа. Запишем физический способ решения задачи.
Учащимся можно предложить составить задачу по рисунку и решить её математическим и физическим способами, 
Физический способ решения.
используя алгоритм:
Линейные функции применяются во многих физических процессах: - в кинематике – это графики пути, перемещения, координаты прямолинейного равномерного движения; скорости, ускорения при прямолинейном равнопеременном движении; - в динамике - графики зависимости Fтяж (m), Fтр (P), Fупр (x),… - в разделе «законы сохранения» - графики зависимостей Еп(h), W(t), p (t),… - в квантовой физике - графики Екин (частота падающего света) в теории фотоэффекта. В 8 классе ученики учатся решать дробные уравнения. Для чего нужны дробные уравнения? Какие задачи приводят к их появлению? В физике это задачи, в которых одна величина выражается через другие при помощи дробного выражения (содержащего переменную в знаменателе дроби). Например: время = сторона прямоугольника = цена = производительность =
В приложении 1 к данной части можно ознакомиться с решением математических задач, которые актуальны и на уроках физики.
При решении задач по физике Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию направление, смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков. На уроках физики учитель дает определение радиус-вектора при изучении механических явлений. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например, скорость, перемещение, импульс, напряженность электрического поля, сила. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов также используют на уроках физики неоднократно, изучая разные темы в разных классах. Интуитивное понимание вектора у учащихся складывается с первых же уроков физики в 7 и 8 классе. Проведем сравнение понятия вектора в физике и математике:
Понимание вектора в физике и математике происходит поэтапно, когда ученики раскрывают и изучают следующие вопросы: В математике: · Координатная прямая. · Координатная плоскость. · Координаты точки. В физике: · Понятие системы отсчета. · Координаты, которыми задается положение тела на прямой, на плоскости, в пространстве, и их количество. Понятие вектор и нулевой вектор, в каком случае проекция вектора на ось считается положительной, отрицательной, равной нулю, - рассматривается как в математике, так и в физике. Координаты вектора в физике рассматриваем относительно перемещения тела. Интеграцию обоих предметов необходимо осуществлять при изучении сложения векторов. В математике это правило треугольника, параллелограмма, многоугольника, произведение векторов. В физике прикладной характер правил сложения векторов виден не при определении перемещения тела, а при сложении скоростей движущегося тела, при вычислении механической работы.
Глубокое понимание вектора и действий с векторами у учеников сложится только посредством интеграции математического и физического определения этих понятий. Рассмотрим пример задачи, при решении которой применяется теорема Пифагора.
На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота? Решение: По теореме Пифагора На уроках физики ученики сталкиваются с теоремой Пифагора чаще всего при изучении механических и оптических явлений. В приложении к данному выступлению можно ознакомиться с подборкой задач на применение векторного анализа и правила треугольника (Приложение 3).
Приложение 1 Задача 1. Коля поехал на дачу на велосипеде, а Миша на мотоцикле. Выехали они одновременно, но так как скорость мотоциклиста на 15 км/час больше скорости велосипедиста, то Миша приехал на 1 часа раньше Коли. Найдите скорость движения каждого мальчика, если расстояние от дома до дачи 30 км. Решение. Так как требуется найти скорости, обозначим меньшую из них буквой Х и заполним таблицу.
Учитывая, что мотоциклист приехал на 2 часа раньше, составим уравнение
Уравнение имеет два корня: х1 = 15, х2 = -30, но второй корень не подходит по смыслу задачи. Ответ: скорость Коли 15 км/час, Миши 30 км/час. При составлении математической модели учителю целесообразно сначала ответить на следующие вопросы совместно с учениками 1. Какой процесс описывается в задаче? 2. Какими величинами характеризуется этот процесс? 3. Как связаны между собой эти величины? 4. Сколько реальных процессов описывается в задаче? 5. Значение каких величин известны? На данном этапе формируются познавательные учебные действия и умение использовать полученную информацию в деятельности, происходит развитие мыслительных операций. В последующем ученикам необходимо решать задания по аналогии, используя алгоритм действий. 6. Значение каких величин сравниваются? 7. Значение каких величин требуется найти? 8. Составить краткую запись условия задачи. 9. Обозначить одну из неизвестных величин переменной х и выразить другие неизвестные величины через х. Решение текстовой задачи на движение состоит из трех этапов: составление математической модели, работы с ней и ответа на вопрос задачи. В этой задаче сравнивались две одноименные величины, применялись три приема: чтобы уравнять две величины, нужно к меньшей из них прибавить разницу между ними, или из большей вычесть разницу, или из большей вычесть меньшую величину. Рассмотрим задачи, описывающие и другие явления физики, не только механические. Задача 2. Электрическое сопротивление одного проводника на 1 Ом больше, чем сопротивление другого. Напряжение 20 Вольт вызывает в параллельно соединенных проводниках ток силой 9 А. Найти сопротивление каждого из проводников. Решение:
Пусть сопротивление одного проводника x (Ом), тогда другого – (x + 1) Ом. Из курса физики известно, что если проводники соединены параллельно, то ток разветвляется, то есть сила тока всей цепи равна сумме сил токов ветвей цепи: Iобщ=I1+I2. По закону Ома: I = U/R. Итак: U/R1+ U/R2=9. Составим уравнение и решим:
Ответ: R1 = 4 Ом, R2 = 5 Ом. Задача 3. Вода массой 10 кг разлита в два сосуда. При нагревании первый сосуд получил 48 ккал, а второй – 12 ккал. После чего температура в первом сосуде оказалась на 10С выше, чем во втором. Сколько килограмм воды находилось в каждом сосуде? (Теплоотдачу в окружающую среду не учитывать). Решение. Количество теплоты Пусть масса воды в первом сосуде х кг, во втором сосуде – (10 – х) кг. По условию ∆Q = 48 ккал, тогда ∆T1 = 48/х, ∆T2 = 12/(10-х). Составим по условию задачи уравнение: 48/х- 12/(10-х) = 1, х ≠0,х≠40. Решаем:
Значение х1 = 62,3 не удовлетворяет условию задачи. Ответ: в первом сосуде было 7,7 кг воды, а во втором – 2,3 кг. Теперь мы рассмотрим несколько физических задач, имеющих практическое значение, решения которых сводятся к решению квадратного уравнения. Совсем скоро дети по физике будут изучать тему «Движение тела под действием силы тяжести». На уроке алгебры при изучении квадратных уравнений учителю рекомендуем вспомнить, какие формулы описывают прямолинейное движение тела по вертикали под действием силы тяжести. Данное движение рассматривается как частный случай равноускоренного движения. Уравнение движения тела имеет вид: H = H = υ = υ = t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>t</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Ускорение свободного падения g =9,8 м/с2 (при решении задач для упрощения расчетов принимают g =10 м/с2). Задача 1. Сколько времени футбольный мяч после удара будет находиться выше 25 м. Начальная скорость мяча 30 м/с? Сопротивлением воздуха пренебречь. Ответ выразите в м/с. Решение:
Мяч пролетает одну и ту же высоту дважды. Один раз – когда летит вверх, и другой – когда мяч летит вниз.
Подобные задачи встречаются и в заданиях ЕГЭ по математике. На это следует обратить внимание учеников. В разделе «самостоятельные работы» мы предлагаем подборку таких задач. Задача 2. Камень падает в шахту. Через 6 секунд слышен звук удара камня о дно шахты. Определите глубину шахты, считая скорость звука равной 330 м/с. Решение: Камень падает вниз на дно шахты, ударяется и звуковая волна от удара камня движется вверх, до высоты слушателя. Поэтому t = tк +tзв , где tк – время падения камня, tзв – время движения звуковой волны.
С другой стороны расстояние, какое проходит звуковая волна определяется по формуле: S = υзв ∙ tзв [м]. Так как глубина шахты и есть, то расстояние, что проходит звуковая волна, то можно приравнять Н=S, и получится уравнение: υзв ∙ tзв = Обозначим время падения камня tк=х, а время движения звуковой волны tзв=у. Составим систему уравнений:
Подставив числовые значения, получим следующую систему уравнений:
Решим систему уравнений методом подстановки: выразим переменную х через у. х =6 – у Тогда система уравнений примет вид:
36 – 12у + у2 = 66у у2 – 78у + 36 = 0 D = 6084 -144 = 5940 y1 = y2 = х = 6 – 0,5 = 5,5 (с) – время падения камня tк. Теперь найдем глубину шахты: H = Ответ: глубина шахты около 151,25 м. Приложение 2
Тип урока: Бинарный урок по физике и математике в 5 классе. Тема Буквенные выражения. Образовательные задачи: 1) заложить первые представления о познаваемости явлений природы; 2) объяснить место физики как науки и показать применимость математического аппарата в ней. Эпиграф: Науку все глубже постигнуть стремись, Познанием вечного жаждой томись. Лишь первых познаний блеснет тебе свет, Узнаешь: предела для знания нет. Фирдоуси (Персидский и таджикский поэт, 940 – 1030 гг). Ход урока Организационный момент. 2. Проверка выполнения домашнего задания. (5 мин) Подготовка к основному этапу. Актуализация. (5 мин) Задача. В полдень термометр показывал температуру t0C, а к полуночи температура опустилась на р0С. Какую температуру показывал термометр в полночь? Составьте выражение и найдите его значение: при t = 25, р = 7. 4. Усвоение новых знаний. (5 мин) Термометр - это прибор, созданный человеком для измерения температуры. Температурой называют величину, которая показывает какое тепло имеет тело, (некоторый объект). Изменение тепла и температуры – это одно из явлений природы, которая изучает наука физика. Также физика изучает другие явления: движение, то есть механическое явление. Еще физика изучает электрические и магнитные явления, свойства света, которые называются оптическими явлениями. Благодаря открытиям в области физики, человечество имеет такую хорошо развитую технику. И конечно такая наука использует математику, как аппарат для расчетов. (Учитель демонстрирует карточки, портреты и другую наглядность по своему усмотрению, продолжает беседу). 5. Творческая работа. (10 мин) Оборудование: Измерительный цилиндр (сосуд со шкалой) с водой и деревянный маленький брусок в форме параллелепипеда. Выполнение работы: 1) Напомнить ученикам, что 1 миллилитр равен 1 кубическому сантиметру. 2) Объяснить коротко, что такое объем, найти объем параллелепипеда по формуле 3) Измерить объем воды в измерительном цилиндре. 4) Опустить в сосуд с водой брусок. 5) Измерить теперь объем воды. 6) Вычислить объем вытесненной воды при погружении бруска. 7) Объем вытесненной воды должен совпасть с объемом бруска (1 мл=1 см3). 8) Сегодня на уроке ученики пятого класса открыли для себя закон Архимеда – один из законов физики. 9) Обозначив объем бруска - V3,объем воды в начале опыта - V1, объем воды с погруженным телом – V1, получим буквенное выражение V3=V2-V1. Вывод: буквенные выражения - одно из средств, необходимое для определения законов физики. 6. Обобщение и систематизация знаний. Остаток времени рекомендуем потратить на решение задач о движении, вспомнить понятие скорости, буквенное выражение, определяющую скорость и т.д. Можно выбрать задачи из учебника или из других источников. Тем самым напомнить еще раз, что физика изучает механические явления – явление движения.
Приложение 3 Задача 1.
Решение: 1) Запишем закон сложения скоростей в векторном виде. 2) Сделаем чертеж, произведя сложение векторов скоростей. 3) Искомый вектор является гипотенузой прямоугольного треугольника. По теореме Пифагора вычислим её, найдя тем самым модуль скорости. 4) Зная, что при прямолинейном равномерном движении модуль перемещения пропорционален скорости, составим пропорцию и найдем модуль искомого перемещения.
Следующие две задачи рекомендуем рассмотреть только после изучения тригонометрических функций острого угла. Задача 2. Скорость лодки относительно течения 10 м/с, скорость течения 5 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж.
Задача 3. С какой силой F (эф) надо удерживать груз весом Р (пэ) на наклонной плоскости, чтобы он не сползал вниз?
Решение: Пусть Задача4. Мяч брошен под углом 450 к горизонту со скоростью 20 м/с с поверхности Земли. Найдите высоту подъема мяча через 2 секунды. Решение:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 973; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.241.118 (0.014 с.) |



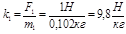



 .
g- ускорение свободного падения
.
g- ускорение свободного падения




 Решение:
Решение:




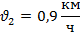

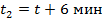





 , т.к.
, т.к. 
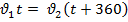



 Ответ:
Ответ: 
 -?
-?









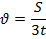

 Ответ:через 2 часа скорость первого равна 5 м/с и скорость второго – 2,5 м/с.
Ответ:через 2 часа скорость первого равна 5 м/с и скорость второго – 2,5 м/с.
 -?
-?

 , скорость =
, скорость =  ;
;
 количество =
количество = 
 время =
время =  .
.
 Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy).
Вспомним формулы для расчета координат тела в любой момент времени (х = х0 + sx, y = y0+ sy).

 Правило параллелограмма.
Правило параллелограмма.
 Правило многоугольника.
Правило многоугольника.

 . Соответствующий многоугольник (треугольник) перемещений выглядит таким образом:
. Соответствующий многоугольник (треугольник) перемещений выглядит таким образом: 

 , то выражение для скорости в любой момент t времени имеет вид:
, то выражение для скорости в любой момент t времени имеет вид:  .
.



 Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела.
Прикладной характер правил сложения векторов виден не только при определении перемещения тела, но и при сложении скоростей движущегося тела.

 Произведение векторов – скалярная величина.
Произведение векторов – скалярная величина.
 Механическая работа – скалярная величина.
Механическая работа – скалярная величина.
 Задача индийского математика XII века Бхаскары.
Задача индийского математика XII века Бхаскары. . Высота тополя равна
. Высота тополя равна  м.
м.

 ; 30x+450=30x+x2+15x; x2+15x-450=0;
; 30x+450=30x+x2+15x; x2+15x-450=0;

 , где С – теплоемкость воды, ∆T – разность температур, показывающая на сколько градусов нагрели воду, m - масса воды, с =1.
, где С – теплоемкость воды, ∆T – разность температур, показывающая на сколько градусов нагрели воду, m - масса воды, с =1.
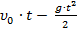 – если тело движется вверх;
– если тело движется вверх; – если тело движется вниз.
– если тело движется вниз. - скорость тела при начальной скорости направленной вниз;
- скорость тела при начальной скорости направленной вниз; - скорость тела при начальной скорости направленной вверх;
- скорость тела при начальной скорости направленной вверх;
 t1= 5, t2= 1
t1= 5, t2= 1 . Ответ: 4 секунды мяч летел выше 25 метров.
. Ответ: 4 секунды мяч летел выше 25 метров.



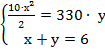


 = 78,5 (с) - не подходит, т.к это время больше 6с.
= 78,5 (с) - не подходит, т.к это время больше 6с. = 0,5(с) – время движения звуковой волны tзв.
= 0,5(с) – время движения звуковой волны tзв. = 151,25 (м).
= 151,25 (м). (объем параллелепипеда равен произведению трех его измерений, то есть длины, ширины и высоты).
(объем параллелепипеда равен произведению трех его измерений, то есть длины, ширины и высоты). Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?
Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?




 – центр тяжести груза, к которому приложена сила
– центр тяжести груза, к которому приложена сила 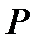 . Разложим вектор
. Разложим вектор  по двум взаимно перпендикулярным направлениям. Сила
по двум взаимно перпендикулярным направлениям. Сила  перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила
перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила  , удерживающая груз,
, удерживающая груз,  должна быть равной по величине и противоположной по направлению силе. Поэтому
должна быть равной по величине и противоположной по направлению силе. Поэтому  .
.
 <
< 


