Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прогрессии. Числовые последовательностиСодержание книги Поиск на нашем сайте
В Вавилонском царстве всеми расчетами занимались писцы, которые принадлежали к высшему сословию. Школа, где обучались писцы, называлась «дом табличек». Для таких школ предназначались специальные математические таблички. Тексты на них можно было разделить на два класса: таблицы и задачники. Среди задач на табличках встречаются задачи на арифметические и геометрические прогрессии. Вавилонские писцы знали правила суммирования n членов арифметической прогрессии:
Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства. Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым. Ариабхатта (V в.) применял формулы общего числа, суммы арифметической прогрессии. Но правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202 г. (Леонардо Пизанский) Сегодня встречается понятие прогрессии в различных областях науки. Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растёт по геометрической прогрессии. Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию. Физика. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывают их ещё на 4 части… – это пример геометрической прогрессии. Биология. Многие организмы обладают интенсивностью размножения в геометрической прогрессии. Известно, что бактерии размножаются давлением: одна бактерия делится на две; каждая из этих двух делится ещё на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий… Интенсивность размножения бактерий используют в пищевой и фармацевтической промышленностях, в сельском и коммунальном хозяйствах, природоохранных мероприятиях. Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии. С решением типичных задачи из различных областей наук, а также использованием первоначальных сведений из теории чисел, теории групп и теории инвариантов в ходе изучения различных предметов можно познакомится самостоятельно в приложение 4. При организации интегрированного обучения видна органическая связь между предметами, обучающиеся почувствуют и полюбят эффект разнообразия, а также у них будет развиваться новое качество - целенаправленно работать и ориентироваться в созданных условиях.
Приложение 1 Задача 1. Коля поехал на дачу на велосипеде, а Миша на мотоцикле. Выехали они одновременно, но так как скорость мотоциклиста на 15 км/час больше скорости велосипедиста, то Миша приехал на 1 часа раньше Коли. Найдите скорость движения каждого мальчика, если расстояние от дома до дачи 30 км. Решение. Так как требуется найти скорости, обозначим меньшую из них буквой Х и заполним таблицу.
Учитывая, что мотоциклист приехал на 2 часа раньше, составим уравнение
Уравнение имеет два корня: х1 = 15, х2 = -30, но второй корень не подходит по смыслу задачи. Ответ: скорость Коли 15 км/час, Миши 30 км/час. При составлении математической модели учителю целесообразно сначала ответить на следующие вопросы совместно с учениками 1. Какой процесс описывается в задаче? 2. Какими величинами характеризуется этот процесс? 3. Как связаны между собой эти величины? 4. Сколько реальных процессов описывается в задаче? 5. Значение каких величин известны? На данном этапе формируются познавательные учебные действия и умение использовать полученную информацию в деятельности, происходит развитие мыслительных операций. В последующем ученикам необходимо решать задания по аналогии, используя алгоритм действий. 6. Значение каких величин сравниваются? 7. Значение каких величин требуется найти? 8. Составить краткую запись условия задачи. 9. Обозначить одну из неизвестных величин переменной х и выразить другие неизвестные величины через х. Решение текстовой задачи на движение состоит из трех этапов: составление математической модели, работы с ней и ответа на вопрос задачи. В этой задаче сравнивались две одноименные величины, применялись три приема: чтобы уравнять две величины, нужно к меньшей из них прибавить разницу между ними, или из большей вычесть разницу, или из большей вычесть меньшую величину. Рассмотрим задачи, описывающие и другие явления физики, не только механические. Задача 2. Электрическое сопротивление одного проводника на 1 Ом больше, чем сопротивление другого. Напряжение 20 Вольт вызывает в параллельно соединенных проводниках ток силой 9 А. Найти сопротивление каждого из проводников. Решение:
Пусть сопротивление одного проводника x (Ом), тогда другого – (x + 1) Ом. Из курса физики известно, что если проводники соединены параллельно, то ток разветвляется, то есть сила тока всей цепи равна сумме сил токов ветвей цепи: Iобщ=I1+I2. По закону Ома: I = U/R. Итак: U/R1+ U/R2=9. Составим уравнение и решим:
Ответ: R1 = 4 Ом, R2 = 5 Ом. Задача 3. Вода массой 10 кг разлита в два сосуда. При нагревании первый сосуд получил 48 ккал, а второй – 12 ккал. После чего температура в первом сосуде оказалась на 10С выше, чем во втором. Сколько килограмм воды находилось в каждом сосуде? (Теплоотдачу в окружающую среду не учитывать). Решение. Количество теплоты Пусть масса воды в первом сосуде х кг, во втором сосуде – (10 – х) кг. По условию ∆Q = 48 ккал, тогда ∆T1 = 48/х, ∆T2 = 12/(10-х). Составим по условию задачи уравнение: 48/х- 12/(10-х) = 1, х ≠0,х≠40. Решаем:
Значение х1 = 62,3 не удовлетворяет условию задачи. Ответ: в первом сосуде было 7,7 кг воды, а во втором – 2,3 кг. Теперь мы рассмотрим несколько физических задач, имеющих практическое значение, решения которых сводятся к решению квадратного уравнения. Совсем скоро дети по физике будут изучать тему «Движение тела под действием силы тяжести». На уроке алгебры при изучении квадратных уравнений учителю рекомендуем вспомнить, какие формулы описывают прямолинейное движение тела по вертикали под действием силы тяжести. Данное движение рассматривается как частный случай равноускоренного движения. Уравнение движения тела имеет вид: H = H = υ = υ = t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>t</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Ускорение свободного падения g =9,8 м/с2 (при решении задач для упрощения расчетов принимают g =10 м/с2). Задача 1. Сколько времени футбольный мяч после удара будет находиться выше 25 м. Начальная скорость мяча 30 м/с? Сопротивлением воздуха пренебречь. Ответ выразите в м/с. Решение:
Мяч пролетает одну и ту же высоту дважды. Один раз – когда летит вверх, и другой – когда мяч летит вниз.
Подобные задачи встречаются и в заданиях ЕГЭ по математике. На это следует обратить внимание учеников. В разделе «самостоятельные работы» мы предлагаем подборку таких задач. Задача 2. Камень падает в шахту. Через 6 секунд слышен звук удара камня о дно шахты. Определите глубину шахты, считая скорость звука равной 330 м/с. Решение: Камень падает вниз на дно шахты, ударяется и звуковая волна от удара камня движется вверх, до высоты слушателя. Поэтому t = tк +tзв , где tк – время падения камня, tзв – время движения звуковой волны.
С другой стороны расстояние, какое проходит звуковая волна определяется по формуле: S = υзв ∙ tзв [м]. Так как глубина шахты и есть, то расстояние, что проходит звуковая волна, то можно приравнять Н=S, и получится уравнение: υзв ∙ tзв = Обозначим время падения камня tк=х, а время движения звуковой волны tзв=у. Составим систему уравнений:
Подставив числовые значения, получим следующую систему уравнений:
Решим систему уравнений методом подстановки: выразим переменную х через у. х =6 – у Тогда система уравнений примет вид:
36 – 12у + у2 = 66у у2 – 78у + 36 = 0 D = 6084 -144 = 5940 y1 = y2 = х = 6 – 0,5 = 5,5 (с) – время падения камня tк. Теперь найдем глубину шахты: H = Ответ: глубина шахты около 151,25 м. Приложение 2
Тип урока: Бинарный урок по физике и математике в 5 классе. Тема Буквенные выражения. Образовательные задачи: 1) заложить первые представления о познаваемости явлений природы; 2) объяснить место физики как науки и показать применимость математического аппарата в ней. Эпиграф: Науку все глубже постигнуть стремись, Познанием вечного жаждой томись. Лишь первых познаний блеснет тебе свет, Узнаешь: предела для знания нет. Фирдоуси (Персидский и таджикский поэт, 940 – 1030 гг). Ход урока Организационный момент. 2. Проверка выполнения домашнего задания. (5 мин) Подготовка к основному этапу. Актуализация. (5 мин) Задача. В полдень термометр показывал температуру t0C, а к полуночи температура опустилась на р0С. Какую температуру показывал термометр в полночь? Составьте выражение и найдите его значение: при t = 25, р = 7. 4. Усвоение новых знаний. (5 мин) Термометр - это прибор, созданный человеком для измерения температуры. Температурой называют величину, которая показывает какое тепло имеет тело, (некоторый объект). Изменение тепла и температуры – это одно из явлений природы, которая изучает наука физика. Также физика изучает другие явления: движение, то есть механическое явление. Еще физика изучает электрические и магнитные явления, свойства света, которые называются оптическими явлениями. Благодаря открытиям в области физики, человечество имеет такую хорошо развитую технику. И конечно такая наука использует математику, как аппарат для расчетов. (Учитель демонстрирует карточки, портреты и другую наглядность по своему усмотрению, продолжает беседу). 5. Творческая работа. (10 мин) Оборудование: Измерительный цилиндр (сосуд со шкалой) с водой и деревянный маленький брусок в форме параллелепипеда. Выполнение работы: 1) Напомнить ученикам, что 1 миллилитр равен 1 кубическому сантиметру. 2) Объяснить коротко, что такое объем, найти объем параллелепипеда по формуле 3) Измерить объем воды в измерительном цилиндре. 4) Опустить в сосуд с водой брусок. 5) Измерить теперь объем воды. 6) Вычислить объем вытесненной воды при погружении бруска. 7) Объем вытесненной воды должен совпасть с объемом бруска (1 мл=1 см3). 8) Сегодня на уроке ученики пятого класса открыли для себя закон Архимеда – один из законов физики. 9) Обозначив объем бруска - V3,объем воды в начале опыта - V1, объем воды с погруженным телом – V1, получим буквенное выражение V3=V2-V1. Вывод: буквенные выражения - одно из средств, необходимое для определения законов физики. 6. Обобщение и систематизация знаний. Остаток времени рекомендуем потратить на решение задач о движении, вспомнить понятие скорости, буквенное выражение, определяющую скорость и т.д. Можно выбрать задачи из учебника или из других источников. Тем самым напомнить еще раз, что физика изучает механические явления – явление движения.
Приложение 3 Задача 1.
Решение: 1) Запишем закон сложения скоростей в векторном виде. 2) Сделаем чертеж, произведя сложение векторов скоростей. 3) Искомый вектор является гипотенузой прямоугольного треугольника. По теореме Пифагора вычислим её, найдя тем самым модуль скорости. 4) Зная, что при прямолинейном равномерном движении модуль перемещения пропорционален скорости, составим пропорцию и найдем модуль искомого перемещения.
Следующие две задачи рекомендуем рассмотреть только после изучения тригонометрических функций острого угла. Задача 2. Скорость лодки относительно течения 10 м/с, скорость течения 5 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж.
Задача 3. С какой силой F (эф) надо удерживать груз весом Р (пэ) на наклонной плоскости, чтобы он не сползал вниз?
Решение: Пусть Задача4. Мяч брошен под углом 450 к горизонту со скоростью 20 м/с с поверхности Земли. Найдите высоту подъема мяча через 2 секунды. Решение:
Теорема Пифагора
Приложение 4 Применение первоначальных сведений из теории чисел, теории групп и теории инвариантов как в математике, так и в физике. На первых уроках по физике в 7 классе учитель обычно раскрывает смысл физический явлений, рассказывает о том, что физика – наука, которая изучает физические явления и процессы. Физика для исследования физических процессов использует математический аппарат исчисления. Нужно подвести детей к тому, что им придется изучить много формул, описывающие физические процессы. И здесь учителю необходимо раскрыть смысл записи больших и малых чисел в стандартном виде. Так как дети еще с пятого класса по математике знают формулу Задача: расстояние от Земли до солнца 150000000 км. За сколько секунд свет от Солнца дойдет до Земли, если скорость света 300000 Решение: Воспользуемся известным определением: расстояние, прошедшее движущимся телом за единицу времени называется скоростью. Значит, нам нужно 150 миллионов километров поделить на 300 тысяч километров. 150 миллионов в стандартной записи имеет вид: Дано: Решение:
Если учитель хочет рассмотреть эту задачу на первых вводных уроках по физике, то ему придется объяснить детям тему «Действия со степенями», которую они будут изучать на уроках математики в 8 классе.
В восьмом классе по математике при изучении темы «Стандартный вид числа» предлагаем ввести названия больших малых чисел и сразу после введения определения «стандартный вид числа»:
Чтобы ввести понятие малых чисел, предлагаем решить следующую задачу. Задача. Масса Земли приближенно равна 6 000 000 000 000 000 000 000 т, а масса атома водорода 0,0000000000000000000017 г. Во сколько раз Земля тяжелее атома водорода? Дано:
Решение: Вначале ученикам нужно объяснить, что а в степени минус эн равен обратной величине а в степени э. Хотя по учебнику Макарычева Юрий Николаевича эта формулу рассматривают в 9 классе. А на уроках физики дети с ней сталкиваются, как только начинают решать серьезные задачи. Итак, вводим формулу:
Вспомним, что при делении степеней с одинаковыми основаниями показатели степени вычитаются.
Даже на вводных уроках по физике бывает так, что учитель не обращает внимания на то, что дети не знают приставок СИ, что их надо запомнить, как таблицу умножения, «на века». Так хотя бы на уроках математики, при изучении темы «стандартное число» или «действия со степенями» необходимо эти приставки заучить наизусть.
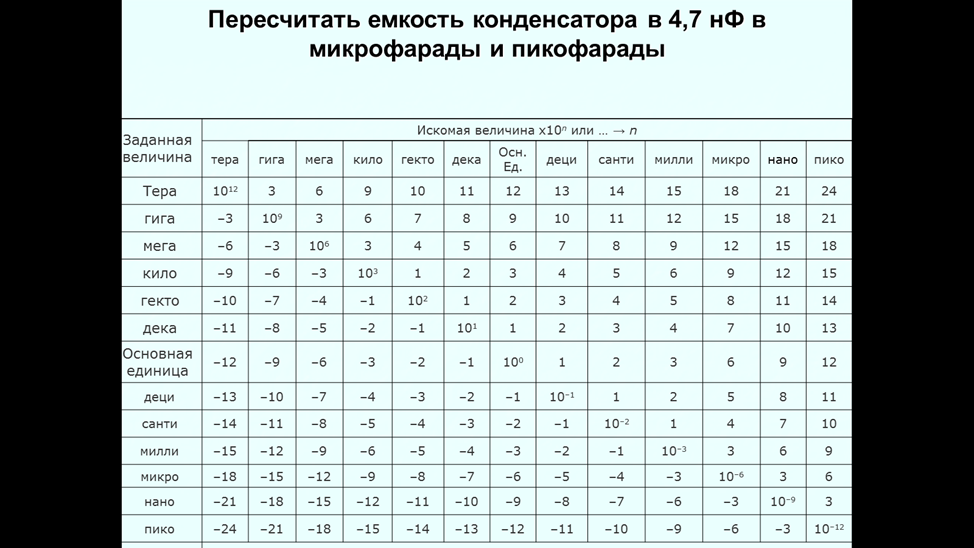
Предлагаем рассмотреть с учениками таблицу пересчета приставок дольных и кратных десятичных единиц физических величин.
1) Для закрепления предлагаем следующую задачу.
Задача: Пересчитать длину волны 0,45 микрометров в метры и нанометры. Решение:
2) Основные сведения о планетах Солнечной системы – планетах земной группы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1028; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.250 (0.013 с.) |

 .
.

 ; 30x+450=30x+x2+15x; x2+15x-450=0;
; 30x+450=30x+x2+15x; x2+15x-450=0;

 , где С – теплоемкость воды, ∆T – разность температур, показывающая на сколько градусов нагрели воду, m - масса воды, с =1.
, где С – теплоемкость воды, ∆T – разность температур, показывающая на сколько градусов нагрели воду, m - масса воды, с =1.
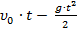 – если тело движется вверх;
– если тело движется вверх; – если тело движется вниз.
– если тело движется вниз. - скорость тела при начальной скорости направленной вниз;
- скорость тела при начальной скорости направленной вниз; - скорость тела при начальной скорости направленной вверх;
- скорость тела при начальной скорости направленной вверх;
 t1= 5, t2= 1
t1= 5, t2= 1 . Ответ: 4 секунды мяч летел выше 25 метров.
. Ответ: 4 секунды мяч летел выше 25 метров.



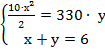


 = 78,5 (с) - не подходит, т.к это время больше 6с.
= 78,5 (с) - не подходит, т.к это время больше 6с. = 0,5(с) – время движения звуковой волны tзв.
= 0,5(с) – время движения звуковой волны tзв. = 151,25 (м).
= 151,25 (м). (объем параллелепипеда равен произведению трех его измерений, то есть длины, ширины и высоты).
(объем параллелепипеда равен произведению трех его измерений, то есть длины, ширины и высоты). Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?
Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?




 – центр тяжести груза, к которому приложена сила
– центр тяжести груза, к которому приложена сила 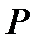 . Разложим вектор
. Разложим вектор  по двум взаимно перпендикулярным направлениям. Сила
по двум взаимно перпендикулярным направлениям. Сила  перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила
перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила  , удерживающая груз,
, удерживающая груз,  должна быть равной по величине и противоположной по направлению силе. Поэтому
должна быть равной по величине и противоположной по направлению силе. Поэтому  .
.









 стоп.
стоп.

 . Решив это уравнение, получаем значение x=12. Ответ: глубина озера составляет 12 метров, длина камыша – 13 метров.
. Решив это уравнение, получаем значение x=12. Ответ: глубина озера составляет 12 метров, длина камыша – 13 метров.

 Решение:
По теореме Пифагора получаем
Решение:
По теореме Пифагора получаем
 .
.

 =
=  . Устанавливают 4 троса.
. Устанавливают 4 троса.  . Ответ: 50 метров троса не хватит, нужно еще 2 метра.
. Ответ: 50 метров троса не хватит, нужно еще 2 метра.
 , то для постановки проблемного вопроса на уроке математике при изучении темы «стандартный вид числа» в 8 классе, можно дать задачу с большими величинами, решаемую с помощью этой формулы. Например:
, то для постановки проблемного вопроса на уроке математике при изучении темы «стандартный вид числа» в 8 классе, можно дать задачу с большими величинами, решаемую с помощью этой формулы. Например: .
. , то есть 150 000 000 =15
, то есть 150 000 000 =15  10 000 000=
10 000 000=  . Несколькими уроками ранее учащиеся изучили действия со степенями:
. Несколькими уроками ранее учащиеся изучили действия со степенями:  Итак, решение задачи:
Итак, решение задачи:






 .
. .
.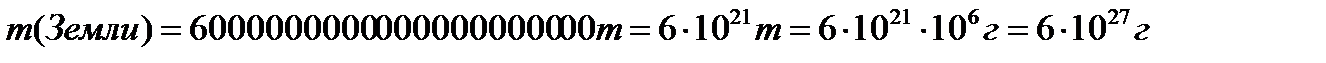 .
.