
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет напряжений при изгибеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Формула для расчета нормальных напряжений при изгибе Рассмотрим изогнутый участок бруса dz (рис. 32.2).
Суммарный изгибающий момент сил упругости в сечении Вспомните свои лучшие путешествия: отзывы. Заработай на Отзывах.
Таким образом, Откуда Е / р = Mn / Jx. Ранее получено После ряда преобразований получим формулу для определения нормальных напряжений в любом слое поперечного сечения бруса:
где Jx — геометрическая характеристика сечения при изгибе. Эпюра распределения нормальных напряжений при изгибе изображена на рис. 32.3.
Отношение Эта величина называется моментом сопротивления сечения при изгибе, или осевым моментом сопротивления. Размерность — мм3. Wx характеризует влияние формы и размеров сечения на прочность при изгибе. Напряжение на поверхности 2. Вращательное движение твердого тела Движение твердого тела, при котором все точки, лежащие на некоторой прямой, принадлежащей телу или неизменно с ним связанной, остаются неподвижными в рассматриваемой системе отсчета, называется вращательным движением. Упомянутая выше прямая называется осью вращения.
Внутренние силовые факторы В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих сил применяют метод сечений: надо мысленно рассечь брус, находящийся в равновесии, на две части и рассмотреть равновесие одной из них.
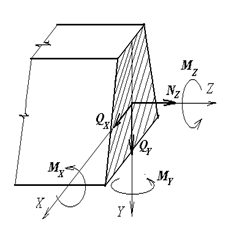
Под действием внешних нагрузок в поперечном сечении бруса возникают следующие внутренние силовые факторы (рис. 2.1):
Nz = N - продольная растягивающая (сжимающая) сила Mz = T - крутящий (скручивающий) момент Qx (Qy) = Q - поперечные силы Mx (My) = M - изгибающие моменты
Рис. 2.1
Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):
Моменты инерции и сопротивления при изгибе бруса прямоугольного сечения Моменты инерции наиболее распространенных фигур Для прямоугольника сечением Выделим в сечении на расстоянии y элементарную площадку: Тогда
Рис. 2.22. Моменты инерции плоских сечений
Аналогично найдем Момент инерции этой фигуры относительно оси x1, находящейся от центральной на расстоянии
Полярный момент кругового кольца относительно центра круга (см. подпункт 2.4.2.4):
Так как эта фигура имеет две взаимно-перпендикулярные оси симметрии, то
а осевые моменты инерции сплошного круга
Формулы (2.53), (2.56) позволяют определить геометрические характеристики сложных плоских сечений путем «разбивки» их на простые. Для наиболее широко распространенных стандартных профилей (двутавр, швеллер, уголок) геометрические характеристики сечений приведены в каталогах на сортовой прокат.
Моменты сопротивлений сечений Моментом сопротивления сечения при изгибе относительно нейтральной оси называется отношение момента инерции относительно центральной оси к расстоянию от оси до наиболее растянутых волокон. Тогда на основании формул (2.59) – (2.62) моменты сопротивлений, мм3:
прямоугольного сечения: кольцевого круга: сплошного круга:
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.228 (0.009 с.) |

 Рис. 32.2
Рис. 32.2
 .
. - осевой момент инерции сечения.
- осевой момент инерции сечения. .
. .
.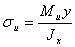 ,
, Рис. 32.3
Рис. 32.3
 .
.
 принято обозначать Wx:
принято обозначать Wx: 
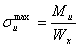 .
.

 (рис. 2.22, а) осевой момент инерции относительно оси x, проходящей через центр тяжести сечения (центральной оси x):
(рис. 2.22, а) осевой момент инерции относительно оси x, проходящей через центр тяжести сечения (центральной оси x):  .
.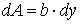 .
. . (2.59)
. (2.59)
 . (2.60)
. (2.60) , согласно уравнению (2.56):
, согласно уравнению (2.56):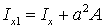 . (2.61)
. (2.61) .
. , (2.62)
, (2.62) . (2.62 а)
. (2.62 а)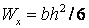 ,
,  ; (2.63)
; (2.63) ; (2.64)
; (2.64) . (2.65)
. (2.65)


