
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр продольных сил NzСтр 1 из 4Следующая ⇒
Виды опорных закреплений
С технической точки зрения опорные закрепления конструкций весьма разнообразны. При формировании расчетной схемы все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).
Рис. 1
В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
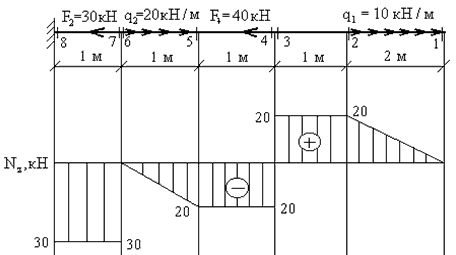
Построение эпюр продольных сил Nz
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
По найденным значениям строим эпюру Nz. Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.
рис. 2
Построение эпюр крутящих моментов Мкр.
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
По найденным значениям строим эпюру Мкр (рис.3,б).
рис. 3 Внутренние силовые факторы В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих сил применяют метод сечений: надо мысленно рассечь брус, находящийся в равновесии, на две части и рассмотреть равновесие одной из них.
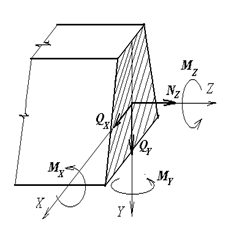
Под действием внешних нагрузок в поперечном сечении бруса возникают следующие внутренние силовые факторы (рис. 2.1):
Nz = N - продольная растягивающая (сжимающая) сила Mz = T - крутящий (скручивающий) момент Qx (Qy) = Q - поперечные силы Mx (My) = M - изгибающие моменты
Рис. 2.1
Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):
Расчет сварных соединений
При расчете сварных соединений необходимо учитывать вид соединения, способ сварки (автоматическая, полуавтоматическая, ручная) и сварочные материалы, соответствующие основному материалу конструкции (табл. 4.2). Расчет стыковых сварных соединений при действии осевой силы
где пределы стыка (например, на технологические планки, см. рис.4.4, б);
Рис. 4.4. Виды сварных стыковых соединений а – прямой стык; б – косой стык; в, г – при разной ширине соединяемых элементов; д, е – при разной толщине соединяемых элементов; ж – однослойный с подваркой корня; 1 – технологические планки; 2 – подварочный шов
При отсутствии физических методов контроля расчетное сопротивление металла сварного соединения по нормам составляет Чтобы соединение было равнопрочным основному элементу, длина шва должна быть больше размера “b” (рис.4.5), поэтому в соединении применяют косой шов, который выполняют с наклоном реза Расчетное сопротивление при сдвиге соединения Если расчетное сопротивление металла шва в стыковомсоединении Напряжения при кручении Принимая во внимание (2.33), закон Гука при кручении можно описать выражением:
В силу гипотезы, что радиусы круглых поперечных сечений не искривляются, касательные напряжения сдвига в окрестностях любой точки тела, находящейся на расстоянии
т.е. пропорциональны расстоянию ее до оси. Значение относительного угла
Сумма элементарных моментов, действующих по всему поперечному сечению А, равна крутящему моменту МZ. Считая, что Интеграл Таким образом,
откуда, угол закручивания единицы длины бруса
Произведение Полный угол закручивания, рад:
Если крутящий момент и момент инерции сечения постоянны по длине
Решив совместно выражения (2.35) и (2.36), получим уравнение
из которого следует, что напряжение в точке поперечного сечения прямо пропорционально расстоянию до центра сечения. При Отношение полярного момента инерции
Общее уравнение динамики Расчет валов на кручение Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна Скручивающий момент равен Если мощность задана в киловаттах, то величина скручивающего момента определяется по формуле
Виды опорных закреплений
С технической точки зрения опорные закрепления конструкций весьма разнообразны. При формировании расчетной схемы все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).
Рис. 1
В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
Построение эпюр продольных сил Nz
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
По найденным значениям строим эпюру Nz. Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.
рис. 2
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1963; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.255 (0.061 с.) |






 , проходящей через центр тяжести соединения, выполняют по формуле
, проходящей через центр тяжести соединения, выполняют по формуле . Отсюда
. Отсюда  (4.1)
(4.1) - наименьшая из толщин соединяемых элементов;
- наименьшая из толщин соединяемых элементов;  - расчетная длина шва, равная полной его длине, уменьшенной на
- расчетная длина шва, равная полной его длине, уменьшенной на  , или полной его длине, если концы шва выведены за
, или полной его длине, если концы шва выведены за - расчетное сопротивление стыковых сварных соединений по пределу текучести (см.СНиП II-23-81*, прил.5);
- расчетное сопротивление стыковых сварных соединений по пределу текучести (см.СНиП II-23-81*, прил.5);  - коэффициент условия работы.
- коэффициент условия работы.
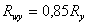 .
.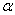 при
при  . Такой шов равнопрочен с основным металлом и не требует проверки прочности. При действии сдвигающей силы Q на стыковой шов, в шве возникают срезывающие напряжения
. Такой шов равнопрочен с основным металлом и не требует проверки прочности. При действии сдвигающей силы Q на стыковой шов, в шве возникают срезывающие напряжения  .
.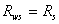 , где
, где  - расчетное сопротивление основного металла на сдвиг.
- расчетное сопротивление основного металла на сдвиг.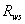 меньше расчетного сопротивления основного металла, проверку выполняют по сечению металла шва.
меньше расчетного сопротивления основного металла, проверку выполняют по сечению металла шва. . (2.34)
. (2.34) от центра (рис. 2.16, б), равны произведению
от центра (рис. 2.16, б), равны произведению , (2.35)
, (2.35) закручивания по формуле (2.35) может быть найдено из условия, что элементарная окружная сила (
закручивания по формуле (2.35) может быть найдено из условия, что элементарная окружная сила (  ) на элементарной площадке размером dA, расположенной на расстоянии
) на элементарной площадке размером dA, расположенной на расстоянии  .
. :
: .
. представляет собой чисто геометрическую характеристику и носит название полярного момента инерции сечения.
представляет собой чисто геометрическую характеристику и носит название полярного момента инерции сечения. , (2.36)
, (2.36) . (2.37)
. (2.37) называется жесткостью сечения бруса при кручении.
называется жесткостью сечения бруса при кручении. . (2.38)
. (2.38) стержня, то полный угол закручивания
стержня, то полный угол закручивания . (2.39)
. (2.39) , (2.40)
, (2.40) . Наибольшие напряжения возникают у наружной поверхности:
. Наибольшие напряжения возникают у наружной поверхности:  .
. к наибольшему радиусу r называется моментом сопротивления сечения кручению
к наибольшему радиусу r называется моментом сопротивления сечения кручению  , мм3:
, мм3:
 (рад/сек), а передаваемая мощность
(рад/сек), а передаваемая мощность 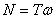 .
.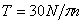 .
. .
.


