Порядок розрахунку статично невизначених систем методом сил.

1) Визначають ступінь статичної невизначеності системи.

2) З заданої статично невизначеної системи утворюють основну шляхом видалення заданого навантаження і всіх зайвих зв’язків.

Щоб привезти основну систему у відповідність з заданою навантажують основну систему заданим навантаженням і зайвими невідомими Х₁, Х₂,...., Х_п, які прикладені по напрямку відкинутих зв’язків. (Основну систему окремо не показують, а тільки навантаження).

3) Складають канонічні рівняння, кожне з яких виражає рівність нулю сумарного переміщення того чи іншого перерізу навантаженої системи по напрямку відкинутого зв’язку, яке виникає від дії заданого навантаження і всіх зайвих невідомих. Число канонічних рівнянь повинно бути рівним числу відкинутих зв’язків.

4) Після того як склали канонічні рівняння переходять до обчислення одиничних σ_ік і вантажних ∆_ір переміщень.

Вантажним називається такий стан основної системи, при якому вона знаходиться лише під дією заданого навантаження.

Одиничним називається такий стан основної системи, при якому вона навантажена тільки однією силою, яка дорівнює одиниці (Х _і=1) та діє в напрямку невідомої реакції (Х_і).

а)Викреслюють вантажний і окремо всі одиничні стани основної системи.

б) Далі будують відповідні їм вантажну М_р і одиничні М₁,М₂,..., М_n епюри згинальних моментів.

в)Обчислюють одиничні σ_ік і вантажні ∆_ір переміщення, за допомогою способу перемноження епюр.

г)Наприклад: щоб визначити переміщення σ₁₁ – потрібно епюру М₁ перемножити саму на себе; σ₁₂ - перемножити епюри М₁ і М₂; ∆_р - М₁ х М_р.

 

44.

При перемноженні епюр необхідно враховувати слідуюче:

а) одиничні переміщення з однаковими індексами - σ₁₁, σ₂₂,…, σ_nn називаються головними; вони ніколи не дорівнюють нулю і завжди додатні, так як при їхньому обчисленні епюри перемножуються самі на себе.

б) одиничні переміщення з різними індексами σ_і1, σ_і2,..., σ_іn називаються другорядними; можуть бути величинами додатніми чи від’ємними, тому що при їх обчисленні перемножуються різні епюри.

в) на основі теореми про взаємні переміщення (теорема Максвела) одиничні переміщення з взаємно переставленими індексами рівні між собою, тобто σ_іn = σn_і .

г) знайдені значення σ_{іn і} ∆_ір підставляють в канонічні рівняння і знаходять зайві невідомі Х₁, Х₂,....Х_п.

д) Завантаживши основну систему заданим навантаженням і вже відомими силами Х₁ = А₁; Х₂ = А₂;....Х_п = А_n , будують епюри Q, M, N, які будуть кінцевими епюрами поперечних сил, згинальних моментів і повздовжніх сил.

Кінцеву епюру згинальних моментів можна отримати і іншим способом, шляхом додавання ординат епюри М_р з відповідними ординатами епюри М₁, помноженими на Х₁, ординатами епюри

М₂, помноженими на Х₂ , і ординатами епюри М_n помноженими на Х_п, тобто:

М_кін.= М_р + М₁ Х₁ +М₂ Х₂ +...+ М_n Х_n.

е) Виконують перевірку розрахунку.

 

 

45.

Перевірка правильності побудови епюр.

Одержані кінцеві епюри необхідно перевірити на правильність побудови.

Перш за все проводиться статична перевірка. Але вона не дає гарантії правильності розрахунку. Наприклад: якщо зайві невідомі визначені невірно, то епюра побудована по цих даних буде вірною, тому статична перевірка буде задовільнятися. Але сам розв’язок в цілому невірний. Помилки при визначені зайвих невідомих можна виявити за допомогою деформаційної чи кінематичної перевірок. Суть в тому що: переміщення в основній системі по напрямку відкинутих зв’язків від сумісної дії всіх зайвих невідомих і заданого навантаження дорівнюють нулю. Це можна зробити шляхом перемноження кінцевої епюри M на відповідну одиничну M₁. При правильному визначенні переміщення будуть рівні нулю.

При перемноженні ординат з однаковими знаками використовують слідуючу формулу:

ωy = l/6 (ас + 4 fq + вd);

де: l – довжина ділянки, на якій перемножаються епюри;

ас - добуток крайніх лівих ординат;

4 fq - добуток середніх ординат;

Вd - добуток крайніх правих ординат.

Якщо ординати, які перемножують з різними знаками, то використовують формулу:

 

ωy = l/6 (2ас + 2 вd + аd +вс).

 

46.

Тема 8. Нерозрізні балки.

 

Загальні відомості.

Нерозрізною називається розташована на опорах статично невизначена балка, яка має безперервну будову по всій довжині з числом прольотів від двох і більше.

Наприклад:

По числу прольотів - двох прольотні, трьох прольотні і т.д. Одна з опор робиться шарнірно нерухомою чи защемленою - всі інші шарнірно рухомі. Опори позначають зліва на право арабськими цифрами 0;1;2;3;4;...п, а прольоти L₁,L₂...L_п. Індекс при довжині кожного прольоту співпадає з номером правої опори цього прольоту. Переріз нерозрізних балок робиться переважно постійним по всій довжині, але, інколи, при великій різниці навантажень в прольотах, вони мають різний переріз. Опори зазвичай розташовуються на одній прямій.

В статичній невизначеності легко переконатися підрахувавши ступінь статичної невизначеності. Для нерозрізних балок знаходиться за формулою:

Л=Соп-3

де: Л - ступінь статичної невизначеності;

Соп -кількість опорних стержнів;

3 -три рівняння рівноваги статики.

Переваги і недоліки.

Переваги: 1)легші, ніж розрізні;

2)забезпечують більш надійний зв'язок опор між собою.

Недоліки: 1)чуттєвість до нерівномірного осідання опор.

 

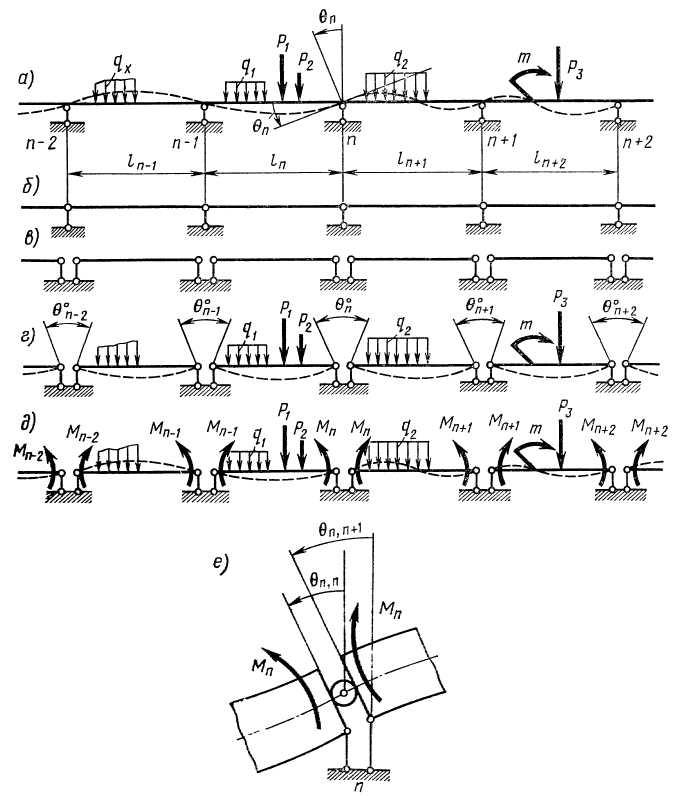
З) Галузь застосування.

Широко використовуються при будівництві громадських і промислових будівель, для влаштування перекриття і підкранових балок, залізно дорожніх і автодорожніх мостів.

4) Рівняння трьох моментів. Нехай розглянемо багато прольотну нерозрізну балку на ділянці між опорами n-2 і n+2.

Пунктирною лінією показана пружна вісь цієї частини балки і кут повороту перерізу на опорі n.

В якості основної системи приймаємо запропоновану французькими інженерами Берто і Клапейроном балку з шарнірами, встановленими над проміжними опорами.

 

47.

 

Але ми знаємо, що в перерізі балки, проведеному через центр шарніра згинальний момент дорівнює нулю. Тому шарніри введені у всі проміжні опорні перерізи даної нерозрізної балки, знищують всі згинальні моменти в цих перерізах.

Тоді дану систему зручніше розглядати, як систему з окремих балочок на шарнірних опорах.

Але ми бачимо, що між основною системою і заданою є розбіжності. Щоб привести основну систему до заданої, навантажуємо основну систему заданим навантаженням.

Тоді, внаслідок наявності шарнірних опор, окремі балочки основної системи вигнуться, а їх опорні перерізи повернуться один відносно другого і утворять так звані кути перелому.

Однак в заданій системі пружна вісь балки представляє собою безперервну плавну криву, а в основній - ні.

Щоб цій умові задовольняла і основна системи, введемо в її опорні перерізи невідомі попарно рівні, але з протилежними напрямками моменти Мn-2; Мn-1; Мn; Мn+1; Мn+2, які будуть замінювати ті внутрішні зусилля, а саме згинальні моменти в опорних перерізах балки, які виявилися рівними нулю в результаті введення шарнірів.

48.

Невідомі моменти прийняті додатніми, тобто направлені так, що повинні викликати розтяг нижніх волокон балки. Одержана в результаті система буде такою ж як задана (якщо дивитись на внутрішні зусилля і переміщення). Тому маючи нерозрізну балку, можемо скласти систему лінійних рівнянь, в кожне з яких ввійдуть три невідомих опорних моменту, які відносяться до кожної пари суміжних прольотів. Всі ці рівняння називаються рівняннями трьох моментів.