З дисципліни «Будівельна механіка»

Курс лекцій

З дисципліни «Будівельна механіка»

 

для студентів стаціонарної та заочної форм навчання

ВНЗ 1-11 рівня акредитації спеціальності

5.06010101 «Будівництво та експлуатація будівель і споруд»

 

 

з номінації: інноватика в організації самостійної

роботи студентів

 

Чернівці, 2010

 

 

Укладач: Карвацька А. В. – викладач спецдисциплін, спеціаліст 11 категорії.

Рецензент: Вилка С. Г. – голова циклової комісії спеціальності

«Будівництво та експлуатація будівель і споруд»

 

Курс лекцій розроблений для студентів стаціонарної та заочної форм навчання для самостійної роботи з вивчення дисципліни «Будівельна механіка» розділ «Статика споруд».

Зміст відповідає робочій програмі. Зібраний і систематизований матеріал, викладений в доступній формі за дотриманням всіх вимог. Теоретичний матеріал супроводжується достатньою кількістю пояснень у вигляді формул і малюнків.

Мета даного посібника – забезпечити студентів і викладачів цілісним матеріалом з вивчення дисципліни «Будівельна механіка» відповідно до діючої програми.

 

Рецензія

На курс лекцій

з дисципліни «Будівельна механіка»

 

Курс лекцій виконано у відповідності з робочою програмою з дисципліни будівельна механіка. Складається з дев’яти тем, які охоплюють не тільки матеріал, вивчений на аудиторних заняттях,

але і теми самостійного вивчення.

Зібраний і систематизований матеріал, викладений в доступній

формі за дотриманням всіх вимог. Теоретичний матеріал супроводжується достатньою кількістю пояснень у вигляді формул і малюнків.

 

Розглянуто на засіданні циклової комісії будівельних дисциплін.

 

Голова комісії:

будівельних дисциплін: Вилка С. Г.

Зміст.

Вступ 3

 

Тема 1. Основні положення. 4

 

Тема 2. Дослідження геометричної незмінності плоских 10

стержневих систем.

 

Тема 3. Багато прольотні статично визначені (шарнірні) балки. 17

 

Тема 4. Cтатично визначені плоскі рами 22

 

Тема 5. Тришарнірні арки. 27

 

Тема 6. Статично визначені плоскі ферми. 31

 

Тема 7. Cтатично невизначені системи. 40

 

Тема 8. Нерозрізні балки. 47

 

Тема 9. Підпірні стіни. 53

 

Висновок. 57

 

Література. 58

 

 

2.

Вступ.

 

Сучасне будівництво вимагає високого рівня знань та навичок. Адже постійно змінюються будівельні матеріали, вдосконалюється технологія ведення робіт, урізноманітнюються проектні рішення. Та потрібно пам’ятати, що будівля чи споруда – це не тільки архітектурна форма або вишукане оздоблення, перш за все – це система конструкцій, яка повинна бути безпечною, міцною, жорсткою під час всього строку експлуатації. Тому будівельникам необхідно знати, яка розрахункова схема системи (балка, рама, арка, ферма), які навантаження діють

(зосереджені чи розподілені) та які внутрішні зусилля виникають

(згинальний момент M і поперечна Q та поздовжня N сили).

Саме такі знання дає дисципліна «Будівельна механіка», а саме розділ «Статика споруд». Проте вивчення цієї дисципліни неможливе без базових знань вищої математики (диференційні рівняння), теоретичної механіки (рівняння рівноваги статики) та опору матеріалів (визначення зусиль Q і M для одно прольотної балки). Водночас будівельна механіка являється передумовою для вивчення такої дисципліни як «Основи розрахунку будівельних конструкцій», оскільки розміри поперечних перерізів елементів підбираються або перевіряються вже прийняті, на основі згинальних моментів та поперечних сил.

Дані методичні рекомендації включають дев’ять тем, що висвітлюють увесь теоретичний матеріал, згідно робочої програми.

 

 

3.

Тема 1. Основні положення.

Загальні відомості.

До теперішнього часу не існує точного визначення поняття споруда. Можливо сказати, що це будівлі з фундаментами, кроквяні і мостові ферми, опори ліній електропередач, резервуари, а також каркаси залізондорожних вагонів, кузови автобусів чи корпуси літаків. В курсі статики споруд під словом «споруда» розуміється сукупність твердих тіл, нерухомо з’єднаних між собою.

До споруд пред’являються слідуючі вимоги:

1) Нерухомість відносно основи (землі) і незмінність геометричної форми на протязі всього строку служби.

2) Міцність, жорсткість і стійкість. Міцність і стійкість гарантують безпеку експлуатації споруди, а достатня жорсткість обмежує її деформацію.

3) Економічність. Визначається найменшими затратами коштів на матеріали і зведення споруди.

Щоб відповідати цим вимогам, треба розраховувати споруди.

Наука, яка вивчає розрахунок споруд на міцність, жорсткість, стійкість незалежно від методу розрахунку, властивості матеріалу (лінійно чи нелінійно пружний, не пружний) і від характеру навантаження (статичне, динамічне) називається будівельною механікою.

Ця наука існувала з давніх часів, але основи будівельної механіки були створені в середині XIX століття в зв’язку з побудовою залізних доріг і будівництвом мостів. Короткий огляд розвитку будівельної механіки вказано в таблиці № 1.

Статикою споруд називають розділ будівельної механіки, який вивчає методи розрахунку будівель на міцність, жорсткість і стійкість при статичному навантаженні.

Статичним називається таке навантаження, величина і положення якого не залежать від часу. Це навантаження передається на споруду спокійно, плавно, без поштовхів і вібрацій, повільно виростаючи від нуля до кінцевого значення і зберігає свою величину довгий час.

 

 

4.

 

«Статика споруд» за своїми методами дослідження і за об'єктами вивчення тісно пов'язана з теоретичною механікою та опором матеріалів.

Всі основні гіпотези і методи визна­чення зусиль та деформацій використовуються в статиці споруд для розрахунку цілих систем.

Статика споруд служить базою для послідуючих дисциплін, які мають справу з інженерними конструкціями. При вивченні їх використовують дані, які даються статикою споруд.

Розрахункова схема -- це спрощене зображення дійсної споруди.

 

Класифікація споруд.

1) В залежності від розташування осей елементів і навантажень:

а ) плоскі споруди, осі елементів яких і навантаження розташовані в одній площині;

 

б) просторові споруди, осі елементів яких розташовані в різних

Опори плоских систем.

Для закріплення споруд до основи служать опори, які бувають

трьох видів:

1) шарнірно рухома; 2) шарнірно нерухома; 3) защемлена.

 

 

1.

Шарнірно рухома опора допускає обертання навколо осі шарніра і поступове переміщення по опорній площині, яка називається опорною подушкою.

 

2.

Шарнірно нерухома опора дозволяє обертання верхнього балансиру навколо осі шарніру і не допускає лінійних переміщень ні по горизонталі, ні по вертикалі.

 

3.

 

Жорстко защемлена опора виключає як лінійні переміщення, так і поворот тіла.

 

 

8.

Таблиця № 1

Прізвище вченого	Дата опублікування	Назва наукової роботи
Клайперон Поль Еміль 1799-1864		Розрахунок нерозрізної балки за допомогою рівняння трьох моментів
Семиколенов		Розрахунок багато прольотних розрізних шарнірних статично визначених балок
Бресс 1822-1883		Розрахунок арок як пружнього тіла
Журавський Дмитро Іванович. 1821-1891		Розробив теорію розрахун-ку плоских ферм. Труд «Про мости розкісної системи ферм Гау»
Ясінській Фелікс Стан. 1856—1899		Теорія розрахунку на стійкість центрально-стиснутих стержнів та ряд других робіт
Максвелл Д.К. 1831-1879		Теорія розрахунку статично невизначених ферм методом сил
Максвелл Кремона		Графічний метод розрахунку статично визначених ферм
Белелюбський Микола Апол. 1845-1918		Видав курс будівельної механіки. Здійснив заміну 70 дер.мостів металічними на Микол. з.д.
Моор Отто 1835-1918		Розрахунок статично невизначених рам методом деформацій
Патон Е.О. 1870-1953 Передерій Г. 1871-1953		Значний вклад в будіве-льну механіку мостів. Зварка. Цільнозварний міст через р.Дніпро в Києві ім. Е.О.Патона

 

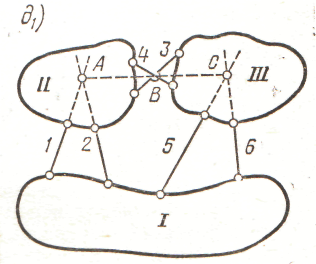
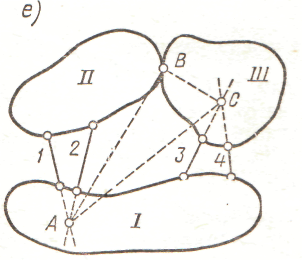
9.

Плоских стержневих систем.

 

Ступінь вільності.

Миттєво змінні системи.

Миттєво змінною називається система, яка допускає без деформації елементів, які її складають, безкінечно малі переміщення цих елементів напротязі дуже малого проміжку часу, після чого система знову стає незмінною.

В реальних умовах переміщення, які виникають в навантажених миттєво змінних системах, внаслідок неправильно розташованих зв’язків і деформації матеріалу переходять в кінцеві, і дуже значні порівнюючи з переміщеннями звичайних незмінних систем, тому миттєво змінні системи в якості будівельних споруд не застосовуються.

Розраховуються вони по окремому спеціальному методу.

13.

Таблиця №2

Допускаються з'єднання дисків з правильно розташованими зв'язками, при цьому утворюються незмінні системи	Не допускаються з'єднання дисків неправильно розташованими зв'язками, оскільки при цьому утворюються миттєво змінні системи
Вузол В можна розглядати як диск з ступеню вільності рівною 2

 

14.

Загальні відомості.

Перекрити декілька прольотів можна окремими простими балками – одно прольотними з шарнірними опорами, чи нерозрізними (тобто розташованими на опорах статично невизначеними балками, які мають суцільну будову по всій своїй довжині, з числом прольотів від двох і більше), чи шарнірними балками.

В курсі опір матеріалів розглядаються три види простих статично визначених балок:

1) одно прольотна балка з шарнірними опорами;

2) одно прольотна балка з консолями;

3) консольна балка з жорсткими опорами.

З цих простих балок можна утворювати більш складну систему, з’єднуючи між собою шарнірами прості балки.

Шарнірною балкою називається геометрично незмінна статично визначена система, складена з розташованих у відповідній послідовності одно прольотних консольних і простих (чи лише одних консольних) балок, з’єднаних між собою шарнірами.

Загальні відомості.

Застосування рамних конструкцій в будівництві дуже різноманітне. Рамні системи утворюють каркаси промислових, цивільних, житлових будинків, сільськогосподарських споруд. Рами можуть входити в склад різних інженерних споруд: естакад, опорних влаштувань мостів, фундаментів під обладнання або використовуються у вигляді окремих конструктивних елементів. Рамні конструкції, як правило, представляють собою просторові системи, але з метою спрощення розрахунку їх розчленовують на окремі плоскі рами. Більшість рам являються статично визначеними. До статично визначених відносяться прості плоскі рами.

Розрахунок рамних систем.

Правила знаків.

Статичний розрахунок рамних систем полягає у визначенні поперечних сил Q, згинальних моментів M та поздовжніх сил N. Що таке поперечна сила та згинальний момент вказано в темі 3 (шарнірна балка), тому в даній темі дамо визначення тільки поздовжньої сили N.

Тема 5. Тришарнірні арки.

Загальні відомості.

Тришарнірна арка являється одним з видів тришарнірних систем. Тришарнірна система складається з двох дисків, з’єднаних між собою одним щарніром і двома шарнірами з основою. Ці шарніри не повинні лежати на одній прямій. Якщо розглядати основу як диск, то тришарнірна система може бути представлена як з’єднання трьох дисків за допомогою трьох шарнірів, які не лежать на одній прямій. Така система геометрично незмінна.

Якщо диски представляють собою стержні криволінійної форми, то система називається тришарнірною аркою, а якщо диски являються прямі чи ламані стержні, то система буде мати назву тришарнірна рама. Якщо дисками являються ферми, то система називається тришарнірною арочною фермою.

 

 

 

 

27.

Термінологія арок.

Для арок існують слідуючі терміни:

1) вісь арки – крива лінія, яка з’єднує центри ваги поперечних перерізів; може бути круглої, коробової, параболічної чи еліптичної форми;

2) п’яти арки – опорні площини П_A і П_B;

3) «замок» чи «ключ» арки – точка вісі, найбільш віддалена від лінії, яка з’єднує центри п’ятових шарнірів А і В.

4) піднімання чи стріла піднімання арки ғ – відстань по вертикалі від

«замка» до лінії, яка з’єднує центри п’ятових шарнірів;

5) проліт арки l - горизонтальна відстань між вертикалями, які проходять через центри п’ятових шарнірів.

В арках навантаження старається розперти кінці, тому на опорах виникає горизонтальна опорна реакція, яка називається «розпором». Саме наявністю цього розпору арка і відрізняється від балки.

Опори арок зазвичай розташовуються на одному рівні. Якщо опори розташовані на різній висоті, що на практиці зустрічається дуже рідко, то арка називається повзучою.

При великому підйомі середньої частини одержується стрілчата арка.

 

Інколи опори трьохшарнірних арок з’єднуються горизонтальним стержнем, який називається затяжкою, яка сприймає розпираючу дію навантаження. В такому випадку одна із опор робиться рухомою. Арки з затяжкою можуть мати масивні опори, так як при вертикальному навантаженні виникають лише вертикальні навантаження, як у балок.

 

28.

 

По матеріалу: арки можуть бути металеві, дерев’яні, кам’яні, бетонні і залізобетонні.

Ми з вами будемо розглядати тільки трьохшарнірні арки з опорами на одному рівні і при вертикальному навантаженні.

Галузь застосування: при будівництві велико прольотних громадських і промислових будівель, ангарів, критих стадіонів, виставкових павільйонів,цехів авіаційних заводів, складів.

 

Розрахунок арочних систем.

Визначення реакцій опор.

Навантаження, прикладені до арки викликають опорні реакції, які складаються з вертикальних V_А і V_В і горизонтальних Н_А і Н_В складових. Горизонтальні складові -- розпори.

 

 

 

29.

 

Оскільки, арочна система являється криволінійним елементом, то при визначенні поперечної та поздовжньої сил необхідно враховувати значення кутів дії сил.

Крива тиску

Раціональна вісь арки.

Вісь арки, яка співпадає з кривою тиску, називається раціональною.

Це можливо у слідуючих випадках:

1) при дії на арку рівномірно розподіленого по всьому прольоті навантаження;

2) коли вісь арки має форму квадратної параболи.

 

 

30.

Загальні відомості.

Фермою називається система, яка складається з прямолінійних стержнів з’єднаних між собою кінцями. Місця з’єднань називаються вузлами.

Вузли виконують жорсткими, зварюючи чи на заклепках. В розрахункових схемах вузли передбачаються шарнірними, цим розрахункові схеми відрізняються від дійсних споруд.

Таке спрощення не викликає значної різниці зусиль в стержнях.

Відстань між центрами опорних вузлів називається прольотом ферми. Стержні утворюють верхній і нижній пояс. Внутрішні стержні утворюють решітку ферми. Вертикальні –стійки, похилі – розкоси.

Відстань між сусідніми вузлами поясів називається

Довжиною панелі –d.

Класифікація ферм.

1) По призначенню:

а) кроквяні, застосовуються для підтримання покриття в промислових, громадських і житлових будівлях;

 

 

31.

 

 

б) ферми залізнодорожних і автодорожних мостів;

в) ферми кранів промислових цехів і складів;

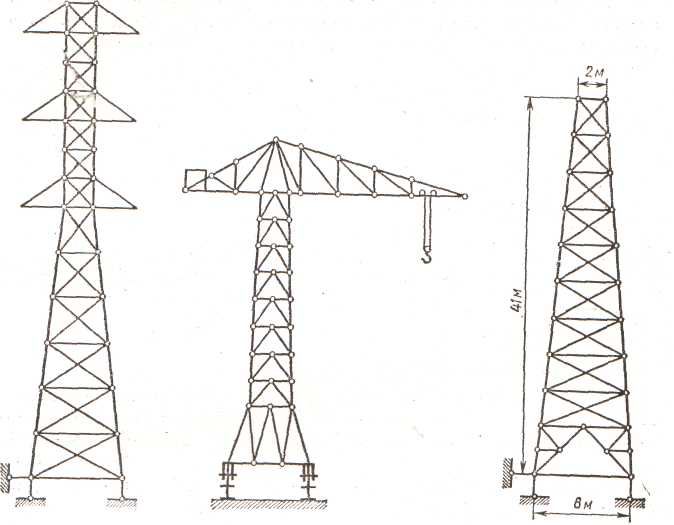
г) мачти високовольтних ліній;

д) ферми будівельних кранів;

е) нафтові вишки;

ж) ферми для легких мостових опор.

 

 

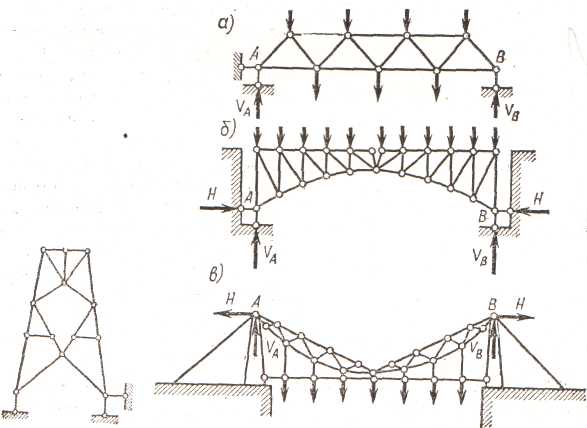
32.

2) По направленню опорних реакцій:

а) безрозпірні чи балочні ферми з вертикальними опорними реакціями;

 

б) розпірні ферми – арочні і висячі, у яких виникають і горизонтальні опорні реакції.

 

 

3) По окресленню поясів:

а) з паралельними поясами:

 

б) з ламаними поясами:

 

 

33.

4) По системі решітки;

а) з розкісною решіткою;

 

б) з трикутною решіткою (решітчасті);

в) ферми з напіврозкісною решіткою.

 

Ці три види решіток називаються простими. З них можна утворити складні або складені, шляхом накладання простих однієї на іншу. Вони називаються двох розкісними і двох решітчастими. Якщо в просту решітку включені додаткові стержні – шпренгелі, то одержуємо шпренгельні ферми.

 

 

 

Загальні відомості.

Зайві зв’язки в статично невизначених системах являються зайвими з точки зору забезпечення незмінності і рівноваги системи, яка без них може бути незмінною і знаходитись у рівновазі. Встановлення таких зв’язків викликається конструктивними особливостями системи.

Наприклад:

Балка АВСД має два зайвих зв’язки. Якщо відкинути В і С або С і Д то в обох випадках балка буде незмінною.

Однак на практиці вона буде непридатною, оскільки у 1 випадку при великому прольоті, у 11 – при великій довжині консолі -- виникнуть великі згинальні моменти.

До статично невизначених відносяться слідуючі системи:

1) Балки: багато прольотні нерозрізні, одно прольотні з одним чи двома

защемленими кінцями.

2) Арки: безшарнірні і двохшарнірні арки. Безшарнірні – тричі статично невизначені, двохшарнірні – один раз.

Дуже рідко зустрічаються одношарнірні арки і арки з защемленими кінцями і шарніром в ключі – двічі статично невизначені.

3) Рами.

4) Ферми: з зайвими стержнями в самій фермі чи з зайвими опорними

стержнями.

40.

Тема 8. Нерозрізні балки.

 

Загальні відомості.

Переваги і недоліки.

Переваги: 1)легші, ніж розрізні;

2)забезпечують більш надійний зв'язок опор між собою.

Недоліки: 1)чуттєвість до нерівномірного осідання опор.

 

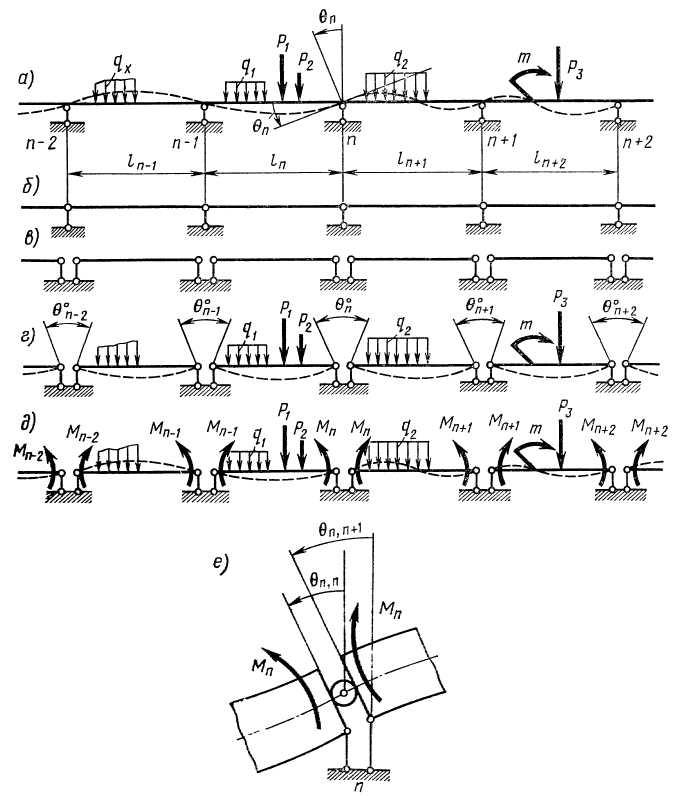
З) Галузь застосування.

Широко використовуються при будівництві громадських і промислових будівель, для влаштування перекриття і підкранових балок, залізно дорожніх і автодорожніх мостів.

4) Рівняння трьох моментів. Нехай розглянемо багато прольотну нерозрізну балку на ділянці між опорами n-2 і n+2.

Пунктирною лінією показана пружна вісь цієї частини балки і кут повороту перерізу на опорі n.

В якості основної системи приймаємо запропоновану французькими інженерами Берто і Клапейроном балку з шарнірами, встановленими над проміжними опорами.

 

47.

 

Але ми знаємо, що в перерізі балки, проведеному через центр шарніра згинальний момент дорівнює нулю. Тому шарніри введені у всі проміжні опорні перерізи даної нерозрізної балки, знищують всі згинальні моменти в цих перерізах.

Тоді дану систему зручніше розглядати, як систему з окремих балочок на шарнірних опорах.

Але ми бачимо, що між основною системою і заданою є розбіжності. Щоб привести основну систему до заданої, навантажуємо основну систему заданим навантаженням.

Тоді, внаслідок наявності шарнірних опор, окремі балочки основної системи вигнуться, а їх опорні перерізи повернуться один відносно другого і утворять так звані кути перелому.

Однак в заданій системі пружна вісь балки представляє собою безперервну плавну криву, а в основній - ні.

Щоб цій умові задовольняла і основна системи, введемо в її опорні перерізи невідомі попарно рівні, але з протилежними напрямками моменти Мn-2; Мn-1; Мn; Мn+1; Мn+2, які будуть замінювати ті внутрішні зусилля, а саме згинальні моменти в опорних перерізах балки, які виявилися рівними нулю в результаті введення шарнірів.

48.

Невідомі моменти прийняті додатніми, тобто направлені так, що повинні викликати розтяг нижніх волокон балки. Одержана в результаті система буде такою ж як задана (якщо дивитись на внутрішні зусилля і переміщення). Тому маючи нерозрізну балку, можемо скласти систему лінійних рівнянь, в кожне з яких ввійдуть три невідомих опорних моменту, які відносяться до кожної пари суміжних прольотів. Всі ці рівняння називаються рівняннями трьох моментів.

 

Тема 9. Підпірні стіни.

Загальні відомості.

Теорія граничної рівноваги.

Існує багато теорій для визначення дій сипучого тіла на підпірну стіну. Найбільш простою з них являється запропонована в 1776 р. Кулоном теорія граничної рівноваги.

Основні припущення:

1. Сипуче тіло розглядається як однорідна маса, яка може сприймати лише зрушувальне та стискаюче зусилля.

2. Приймають, що підпірна стіна під тиском маси сипучого тіла починає зміщуватися і в цей момент сприймає так званий
активний тиск грунту.

Активним тиском (нопором) грунту Е_а називають ту найбільшу дію, яку може спричинити на підпірну стіну маса сипучого тіла разом з розташованим на ній навантаженням в момент початку зміщення стіни.

Вважають, що одночасно зі зміщенням стіни частина сипучого тіла починає сповзати по деякій поверхні, яка називається поверхнею обвалювання. Цю поверхню для спрощення розрахунків приймають за площину. Клин сипучого тіла, утворений поверхнею підпірної стіни і площиною обвалення називаю призмою обвалення.

 

 

54.

 

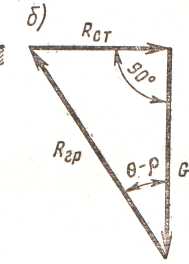
3. Призму обвалення розглядають як абсолютно тверде тіло, що дозволяє замінювати діючі на неї об'ємні і поверхневі сили їх рівнодіючими: Q, R_ст, R_гр.

4. Приймають, що стіна має необмежену довжину, в плані являється
прямолінійною і тиск постійний по всій довжині стіни.

Висновок

Курс лекцій з дисципліни «Будівельна механіка» розроблено для самостійного вивчення студентами стаціонарної і заочної форм навчання. Теми відповідають діючій робочій програмі.

 

 

57.

Література

1) Жемочкин Б. Н., Пащевский Д. П. Статика сооружений. –

М.: Госстройздат. 1959.

 

2) Мухин Н. В. Статика сооружений в примерах. – М., 1979.

 

 

3) Мухин Н. В., Першин А. Н., Шалиман Б. А. Статика сооружений. – М.: Высшая школа, 1979.

 

4) Протаев Л. П., Петров А. А., Портаев В. Л. Техническая механіка. – М.: Стройздат, 1987.

 

 

5) Тимко И. А. Статика сооружений. – Харьков:

Издательство Харьковского университета, 1989.

 

58.

Шарнірною балкою називається геометрично незмінна статично визначена система, складена з розташованих у відповідній послідовності одно прольотних консольних і простих (чи лише одних консольних) балок, з’єднаних між собою шарнірами.

Розрахунок рамних систем.

Правила знаків.

 

Статичний розрахунок рамних систем полягає у визначенні поперечних сил Q, згинальних моментів M та поздовжніх сил N. Що таке поперечна сила та згинальний момент вказано в темі 3 (шарнірна балка), тому в даній темі дамо визначення тільки поздовжньої сили N.

Тема 5. Тришарнірні арки.

Загальні відомості.

Тришарнірна арка являється одним з видів тришарнірних систем. Тришарнірна система складається з двох дисків, з’єднаних між собою одним щарніром і двома шарнірами з основою. Ці шарніри не повинні лежати на одній прямій. Якщо розглядати основу як диск, то тришарнірна система може бути представлена як з’єднання трьох дисків за допомогою трьох шарнірів, які не лежать на одній прямій. Така система геометрично незмінна.

Якщо диски представляють собою стержні криволінійної форми, то система називається тришарнірною аркою, а якщо диски являються прямі чи ламані стержні, то система буде мати назву тришарнірна рама. Якщо дисками являються ферми, то система називається тришарнірною арочною фермою.

 

 

 

 

27.

Термінологія арок.

Для арок існують слідуючі терміни:

1) вісь арки – крива лінія, яка з’єднує центри ваги поперечних перерізів; може бути круглої, коробової, параболічної чи еліптичної форми;

2) п’яти арки – опорні площини П_A і П_B;

3) «замок» чи «ключ» арки – точка вісі, найбільш віддалена від лінії, яка з’єднує центри п’ятових шарнірів А і В.

4) піднімання чи стріла піднімання арки ғ – відстань по вертикалі від

«замка» до лінії, яка з’єднує центри п’ятових шарнірів;

5) проліт арки l - горизонтальна відстань між вертикалями, які проходять через центри п’ятових шарнірів.

В арках навантаження старається розперти кінці, тому на опорах виникає горизонтальна опорна реакція, яка називається «розпором». Саме наявністю цього розпору арка і відрізняється від балки.

Опори арок зазвичай розташовуються на одному рівні. Якщо опори розташовані на різній висоті, що на практиці зустрічається дуже рідко, то арка називається повзучою.

При великому підйомі середньої частини одержується стрілчата арка.

 

Інколи опори трьохшарнірних арок з’єднуються горизонтальним стержнем, який називається затяжкою, яка сприймає розпираючу дію навантаження. В такому випадку одна із опор робиться рухомою. Арки з затяжкою можуть мати масивні опори, так як при вертикальному навантаженні виникають лише вертикальні навантаження, як у балок.

 

28.

 

По матеріалу: арки можуть бути металеві, дерев’яні, кам’яні, бетонні і залізобетонні.

Ми з вами будемо розглядати тільки трьохшарнірні арки з опорами на одному рівні і при вертикальному навантаженні.

Галузь застосування: при будівництві велико прольотних громадських і промислових будівель, ангарів, критих стадіонів, виставкових павільйонів,цехів авіаційних заводів, складів.

 

Розрахунок арочних систем.

Визначення реакцій опор.

Навантаження, прикладені до арки викликають опорні реакції, які складаються з вертикальних V_А і V_В і горизонтальних Н_А і Н_В складових. Горизонтальні складові -- розпори.

 

 

 

29.

 

Оскільки, арочна система являється криволінійним елементом, то при визначенні поперечної та поздовжньої сил необхідно враховувати значення кутів дії сил.

Крива тиску

Раціональна вісь арки.

Вісь арки, яка співпадає з кривою тиску, називається раціональною.

Це можливо у слідуючих випадках:

1) при дії на арку рівномірно розподіленого по всьому прольоті навантаження;

2) коли вісь арки має форму квадратної параболи.

 

 

30.

Довжиною панелі –d.

 

 

а) з паралельними поясами:

 

б) з ламаними поясами:

 

 

1.

Нерозрізні балки.

 

Загальні відомості.

Перекрити декілька прольотів можна окремими простими балками – одно прольотними з шарнірними опорами, чи нерозрізними (тобто розташованими на опорах статично невизначеними балками, які мають суцільну будову по всій своїй довжині, з числом прольотів від двох і більше), чи шарнірними балками.

В курсі опір матеріалів розглядаються три види простих статично визначених балок:

1) одно прольотна балка з шарнірними опорами;

2) одно прольотна балка з консолями;

3) консольна балка з жорсткими опорами.

З цих простих балок можна утворювати більш складну систему, з’єднуючи між собою шарнірами прості балки.

Шарнірною балкою називається геометрично незмінна статично визначена система, складена з розташованих у відповідній послідовності одно прольотних консольних і простих (чи лише одних консольних) балок, з’єднаних між собою шарнірами.

Загальні відомості.

Застосування рамних конструкцій в будівництві дуже різноманітне. Рамні системи утворюють каркаси промислових, цивільних, житлових будинків, сільськогосподарських споруд. Рами можуть входити в склад різних інженерних споруд: естакад, опорних влаштувань мостів, фундаментів під обладнання або використовуються у вигляді окремих конструктивних елементів. Рамні конструкції, як правило, представляють собою просторові системи, але з метою спрощення розрахунку їх розчленовують на окремі плоскі рами. Більшість рам являються статично визначеними. До статично визначених відносяться прості плоскі рами.

Розрахунок рамних систем.

Правила знаків.

Статичний розрахунок рамних систем полягає у визначенні поперечних сил Q, згинальних моментів M та поздовжніх сил N. Що таке поперечна сила та згинальний момент вказано в темі 3 (шарнірна балка), тому в даній темі дамо визначення тільки поздовжньої сили N.

Тема 5. Тришарнірні арки.

Загальні відомості.

Тришарнірна арка являється одним з видів тришарнірних систем. Тришарнірна система складається з двох дисків, з’єднаних між собою одним щарніром і двома шарнірами з основою. Ці шарніри не повинні лежати на одній прямій. Якщо розглядати основу як диск, то тришарнірна система може бути представлена як з’єднання трьох дисків за допомогою трьох шарнірів, які не лежать на одній прямій. Така система геометрично незмінна.

Якщо диски представляють собою стержні криволінійної форми, то система називається тришарнірною аркою, а якщо диски являються прямі чи ламані стержні, то система буде мати назву тришарнірна рама. Якщо дисками являються ферми, то система називається тришарнірною арочною фермою.

 

 

 

 

27.

Термінологія арок.

Для арок існують слідуючі терміни:

1) вісь арки – крива лінія, яка з’єднує центри ваги поперечних перерізів; може бути круглої, коробової, параболічної чи еліптичної форми;

2) п’яти арки – опорні площини П_A і П_B;

3) «замок» чи «ключ» арки – точка вісі, найбільш віддалена від лінії, яка з’єднує центри п’ятових шарнірів А і В.

4) піднімання чи стріла піднімання арки ғ – відстань по вертикалі від

«замка» до лінії, яка з’єднує центри п’ятових шарнірів;

5) проліт арки l - горизонтальна відстань між вертикалями, які проходять через центри п’ятових шарнірів.

В арках навантаження старається розперти кінці, тому на опорах виникає горизонтальна опорна реакція, яка називається «розпором». Саме наявністю цього розпору арка і відрізняється від балки.

Опори арок зазвичай розташовуються на одному рівні. Якщо опори розташовані на різній висоті, що на практиці зустрічається дуже рідко, то арка називається повзучою.

При великому підйомі середньої частини одержується стрілчата арка.

 

Інколи опори трьохшарнірних арок з’єднуються горизонтальним стержнем, який називається затяжкою, яка сприймає розпираючу дію навантаженн