
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные уравнения, описывающие адсорбционное равновесиеСодержание книги
Поиск на нашем сайте
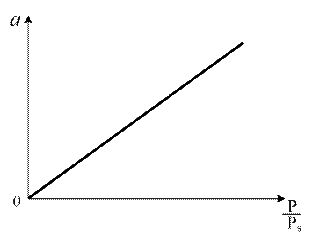
1. Уравнение Генри. При малых значениях Р газа величина адсорбции прямопропорциональна давлению: а = КГ P, (1.4) где К Г − константа Генри. Изотерма Генри представлена на рис. 1.4.
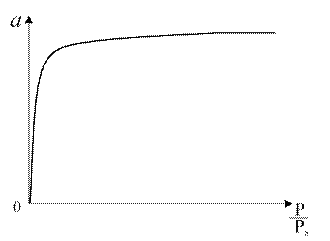
Рис. 1.4. Изотерма Генри Область действия закона Генри мала из-за неоднородности поверхности адсорбентов. С ростом Р наблюдаются отклонения от линейной зависимости. Уравнением Генри описывается начальный участок изотермы для слабо сорбирующихся газов (азот, водород, метан и др.). 2. Уравнение Ленгмюра. Теоретическая интерпретация изотерм типа I для адсорбции на плоской поверхности адсорбента впервые была выполнена американским физиком И. Ленгмюром в 1916 г. и их стали называть ленгмюровскими (синоним: выпуклыми). Изотерма Ленгмюра приведена на рис. 1.5. Изотермы Ленгмюра очень часто встречаются в адсорбционных системах, даже в тех случаях, когда допущения теории Ленгмюра не выполняются или выполняются не полностью.
Рис. 1.5. Изотерма Ленгмюра
Основные положения, лежащие в основе вывода уравнения изотермы адсорбции Ленгмюра следующие: · поверхность адсорбента однородна, т. е. теплота адсорбции на разных участках поверхности одинакова; · теплота адсорбции не зависит от присутствия других адсорбированных молекул, следовательно, можно пренебречь взаимодействием адсорбированных молекул между собой; · молекулы не могут адсорбироваться на молекулах первого слоя и предельная адсорбция аm наблюдается при плотной упаковке адсорбированных молекул на поверхности в слое толщиной в одну молекулу. Уравнение Лэнгмюра: где аm – предельная величина адсорбции, отвечающая плато на изотерме; где b 0 – энтропийный фактор. В области малых давлений (bp << 1) уравнение Ленгмюра переходит в уравнение Генри: а = КГ P, где КГ = b аm. И действительно, нередко экспериментальные изотермы имеют более или менее протяжённый линейный участок при малых количествах адсорбированного вещества.
В области больших давлений (bp >>1) a = аm – уравнение отвечает состоянию насыщения, когда вся поверхность адсорбента покрыта мономолекулярным слоем. Для определения величины аm удобно построить линейный график (рис. 1.6) в координатах:
Рис. 1.6. Изотерма адсорбции в координатах линейной формы уравнения Лэнгмюра
Линейность изотермы в координатах уравнения (1.7) является обязательным условием при доказательстве правомерности применения к системе теории мономолекулярной адсорбции. Тангенс угла наклона прямой и отрезок, отсекаемый прямой на оси ординат, позволяют вычислить константы а m и b. Величина а m представляет интерес не сама по себе, а как средство вычисления важнейшей характеристики адсорбентов – удельной поверхности. Если известна площадка ω, которую занимает одна молекула в плотном монослое, то можно рассчитать удельную поверхность S уд адсорбента по уравнению: S уд = а m NA ω, (1.8) где NA – число Авогадро (6,02 ∙1023 моль–1). Уравнение Лэнгмюра для определения удельной поверхности адсорбента может быть применено к системам, в которых процесс не осложняется полимолекулярной адсорбцией, адсорбцией в микропорах и капиллярной конденсацией. Эти условия соблюдаются при адсорбции газов при температурах выше критической на непористых или крупнопористых адсорбентах. 3. Уравнение БЭТ. Большинство адсорбционных систем описывается изотермами, для которых характерен резкий подъём при относительном давлении
Рис. 1.7. Изотерма адсорбции азота на силикагеле КСС при 77 К
Теория полимолекулярной адсорбции Брунауэра, Эммета и Теллера, получившая название теории БЭТ, основана на модели адсорбционного процесса, предложенной Ленгмюром. Авторы теории оставили два первых положения Ленгмюра, но ввели новые допущения:
· каждая молекула предыдущего слоя представляет собой возможный активный центр для адсорбции молекулы следующего адсорбционного слоя (адсорбция многослойна); · теплота адсорбции во всех слоях выше первого равна скрытой теплоте конденсации λ; · первый слой адсорбата образуется в результате действия сил Ван-дер Вальса между адсорбентом и адсорбатом, последующие в результате конденсации; коэффициенты испарения и конденсации во всех слоях выше первого одинаковы; · когда Р становится равным давлению насыщенного пара, пар адсорбата конденсируется так же, как конденсируется обычная жидкость на адсорбированной пленке. Три последних допущения теории БЭТ связаны с характером сил, действующих между адсорбционными слоями. Они приняли, что эти силы подобны ван-дер-ваальсовым силам, обусловливающим конденсацию, и, следовательно, теплота адсорбции во всех слоях, кроме первого, равна теплоте конденсации. Мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поверхностные силы могут действовать на второй, третий и последующие адсорбционные слои. Если в области образования мономолекулярного слоя величина адсорбции замедляет свой рост с повышением Р, то в области близкой к Ps она резко начинает возрастать и адсорбция заканчивается объёмной конденсацией пара при Р=Рs. Уравнение БЭТ для паров: где а m и C – константы. Константа С непосредственно связана с чистой мольной теплотой адсорбции, соответствующей разности теплоты адсорбции в первом слое Q 1 и мольной теплоты конденсации пара адсорбтива λ: Последнее уравнение используют для вычисления оценочного значения чистой теплоты адсорбции из экспериментальных данных [1]: Q1 − λ = RT ln C (1.10a). Уравнение (1.9) используется для определения удельной поверхности S уд различных пористых тел. При этом нужно помнить, что для микропористых тел уравнение БЭТ соблюдается в интервале относительных давлений: Определение удельной поверхности проводят, используя экспериментальную изотерму адсорбции стандартного пара на исследуемом образце. Обычно при измерении S уд в качестве стандартного пара используют азот или бензол. В случае азота опыт проводят при 77 К, бензола − при 293 К. Величина посадочной площадки молекулы азота практически на всех телах составляет где а m − ёмкость монослоя, г/г; NA – число Авогадро (6,02∙1023, моль−1); М – молекулярная масса азота (28 г/моль), ω – площадь посадочной площадки азота (0,162 . 10−18 м2). При обработке экспериментальных результатов уравнение БЭТ используют в линейной форме: Константы аm и C находят графоаналитическим методом (рис. 1.8) по отрезку, отсекаемому на ординате и тангенсу угла наклона прямой.
Рис. 1.8. Изотермы адсорбции в координатах уравнения БЭТ
При описании адсорбции веществ из растворов используют уравнение типа БЭТ, линейная форма которого имеет вид:
, (1.13)
где K − постоянная для данной адсорбционной системы, непосредственно связанная с теплотой и энтропией адсорбции, с s − концентрация насыщенного раствора адсорбата, ммоль/л; ср − концентрация равновесного раствора, ммоль/л; а – равновесная величина адсорбции, моль/г; а m − ёмкость монослоя молекул адсорбата, покрывающего поверхность адсорбента, моль/г. На рис. 1.9 приведены: (а) − изотерма адсорбции фенола на активированном угле СКТ при 298 К и (б) − эта же изотерма в координатах уравнения БЭТ.
Модель БЭТ неоднократно критиковали, поскольку трудно представить себе абсолютно однородные поверхности. Кроме того, реальные экспериментальные данные свидетельствуют о боковых взаимодействиях адсорбированных молекул между собой. Некоторые исследователи пытались усовершенствовать теорию БЭТ или получить другие модельные изотермы, однако и по сей день метод БЭТ является основным для определения удельной поверхности твердых тел, в том числе адсорбентов и катализаторов. Следует отметить, что адсорбционный метод является практически единственным способом определения величины поверхности непористых порошков и лучшим методом расчета внутренней поверхности пористых твёрдых тел, если, конечно, поры доступны по своим размерам для адсорбции исследуемых молекул. Другие теории позволяют рассчитать из изотерм адсорбции такие геометрические параметры, как объём и размер пор адсорбентов. 4. Уравнение Дубинина – Радушкевича. Для описания адсорбционного равновесия хорошо адсорбирующихся веществ на микропористых сорбентах широко применяется уравнение Дубинина – Радушкевича [4-6]: где а – равновесная величина адсорбции; а 0 – предельная величина адсорбции в микропорах, отвечающая заполнению всего адсорбционного пространства микропор адсорбированными молекулами; Е 0 – характеристическая энергия адсорбции стандартного пара; β– коэффициент подобия, выражающий отношение характеристических энергий адсорбции стандартного и рассматриваемого паров; а 0 = W 0 / υ*; W 0 – общий объём микропор; υ *– мольный объём адсорбата; А − дифференциальная мольная работа адсорбции.
Развивая теорию объемного заполнения микропор, М. М. Дубинин и В. А. Астахов предложили более общее уравнение адсорбции на микропористых адсорбентах, в котором распределение степени заполнения объёма микропор (a /а 0) по дифференциальной мольной работе адсорбции определяется распределением Вейбула: где n − целые числа (от 2 до 6). Таким образом, уравнение Дубинина–Радушкевича является частным случаем уравнения Дубинина–Астахова, когда n = 2. На основании экспериментальной изотермы адсорбции стандартного пара можно рассчитать параметры а 0 и Е 0.
Уравнение (1.15) представляют в линейной форме:
причём отрезок, отсекаемый прямой на оси ординат (в координатах Если показатель степени n известен (например, n равен 2 для активных углей и 3 для цеолитов), то из графика легко определяются предельная величина адсорбции а 0 и характеристическая энергия адсорбции Е 0 на основании одной экспериментальной изотермы адсорбции (рис. 1.10).
Рис. 1.10. Схема определения параметров уравнения Дубинина–Радушкевича
Отклонения от линейной зависимости в области малых величин адсорбции связано с тем, что уравнение (1.15) выполняется при Определив а 0, можно рассчитать W 0, зная мольный объём υ* или плотность адсорбата. Параметры уравнения W 0и Е 0 определяются из изотерм адсорбции стандартных паров бензола при 293 К или азота при 77 К.
|
||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.108 (0.013 с.) |

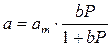 , (1.5)
, (1.5)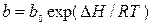 , (1.6)
, (1.6)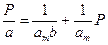 (1.7)
(1.7)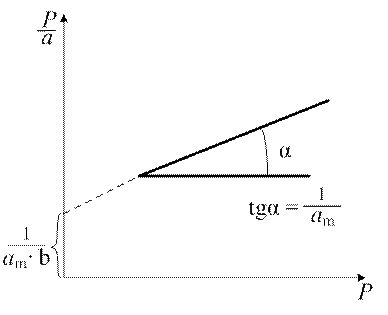
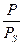 > 0,2, связанный с образованием второго и последующих слоев молекул, покрывающих молекулы первого слоя (рис. 1.7).
> 0,2, связанный с образованием второго и последующих слоев молекул, покрывающих молекулы первого слоя (рис. 1.7).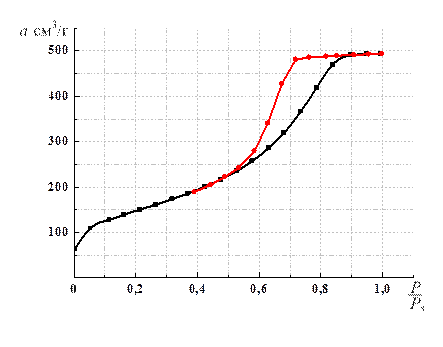
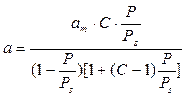 , (1.9)
, (1.9)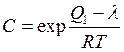 (1.10)
(1.10)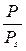 < 0,3. При
< 0,3. При 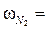 0,162 . 10−18 м2, причём плотность упаковки молекул в адсорбированном слое соответствует их упаковке в нормальной жидкости. Расчёт S уд [м2/г], ведут по уравнению (1.11):
0,162 . 10−18 м2, причём плотность упаковки молекул в адсорбированном слое соответствует их упаковке в нормальной жидкости. Расчёт S уд [м2/г], ведут по уравнению (1.11):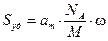 , (1.11)
, (1.11) (1.12)
(1.12)
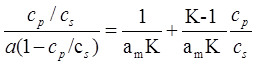
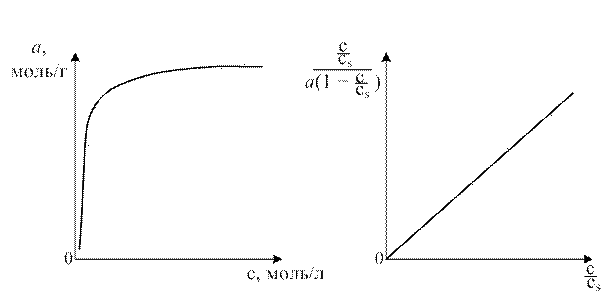 Рис. 1.9. Изотермы адсорбции фенола на активированном угле СКТ при 298 К а) в координатах а = f(c); б) в координатах уравнения БЭТ
Рис. 1.9. Изотермы адсорбции фенола на активированном угле СКТ при 298 К а) в координатах а = f(c); б) в координатах уравнения БЭТ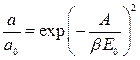 , (1.14)
, (1.14)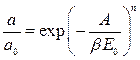 , (1.15)
, (1.15)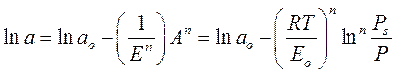 , (1.16)
, (1.16)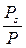 ), равен ln а 0, а угловой коэффициент прямой равен
), равен ln а 0, а угловой коэффициент прямой равен 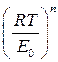 .
.
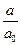 < 0,1. Отклонения в области больших величин адсорбции проявляются в случае микропористых адсорбентов с заметно развитой поверхностью мезопор за счёт дополнительной адсорбции на этой поверхности при относительных давлениях близких к единице.
< 0,1. Отклонения в области больших величин адсорбции проявляются в случае микропористых адсорбентов с заметно развитой поверхностью мезопор за счёт дополнительной адсорбции на этой поверхности при относительных давлениях близких к единице.


