Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адсорбционно-кинетические методы изучения механизмов диффузииСодержание книги
Поиск на нашем сайте
Известны две простейшие схемы изучения кинетики адсорбции. Они иллюстрированы рис. 3.1 [2].
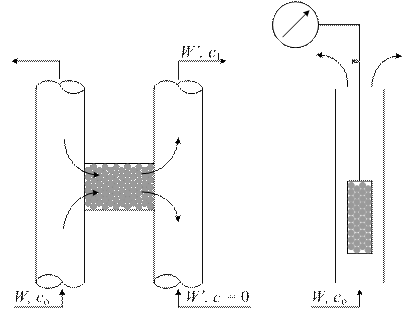
а б Рис. 3.1. Схемы установок для экспериментального изучения кинетики адсорбции: а – Н-образный прибор, б – измерительная ячейка с пружинными весами Согласно первой из них (рис. 3.1а), гранулу отрегенерированного адсорбента помещают в трубочку − «перекладину» Н-образного прибора. По вертикальным трубкам прибора двигаются потоки газа. Левый поток – это смесь газа-носителя и газа-адсорбтива, диффузию которого изучают. Правый поток – чистый газ-носитель. Адсорбтив диффундирует через гранулу, его концентрацию измеряют на входе в левую трубку (с 0) и на выходе из правой трубки (с 1). Скорость миграции адсорбтива Р описывается первым законом Фика: или где D – коэффициент диффузии, выраженный в концентрационных единицах подвижной фазы, De – эффективный коэффициент диффузии, м2/с, выраженный в концентрационных единицах неподвижной фазы, S – площадь гранулы, нормальная к направлению диффузии, l – координата по длине гранулы. Предполагается, что значения с и а равновесны. Заменяя производные конечными разностями, например: где L – длина гранулы, вычисляют D и De. Соотношение между ними: или для линейной изотермы: где К Г – коэффициент Генри. Недостаток схемы, приведенной на рис. 3.1а, заключается в том, что в опытах, выполненных по этой схеме, в сущности, измеряется коэффициент проницаемости сквозных транспортных пор в грануле. Тупиковые поры, в том числе микропоры, в которых происходит адсорбция, этой методикой не учитываются. На рис. 3.1б к коромыслу весов прикреплена гранула адсорбента, вся конструкция помещена в поток несорбирующегося газа, содержащего адсорбтив в концентрации с о. Как только начнется процесс адсорбции, весы будут фиксировать постепенное увеличение веса гранулы. Оно будет продолжаться до тех пор, пока величина адсорбции не достигнет значения, равновесного концентрации адсорбтива в потоке. Обозначим текущую величину адсорбции через а, равновесную − через а о. Тогда отношение γ = а/а о есть степень отработки емкости сорбента, а её зависимость от времени γ = γ (t), называемая кинетической кривой, является кинетической характеристикой процесса, где t – время. Математический аппарат для обработки кинетической кривой и вычисления ее параметра – коэффициента диффузии заимствован из теории теплопроводности. Процесс диффузии в однородное сферическое зерно адсорбента, подобный процессу нагрева (охлаждения) однородной сферической гранулы, при начальных условиях Т = const и с = с s = const записывается дифференциальным уравнением, которое носит название второго закона Фика: где с – концентрация адсорбата в газовой фазе гранулы адсорбента; r – текущий радиус гранулы. Решение уравнения (3.4) при линейной изотерме адсорбции даёт следующее интегральное выражение:
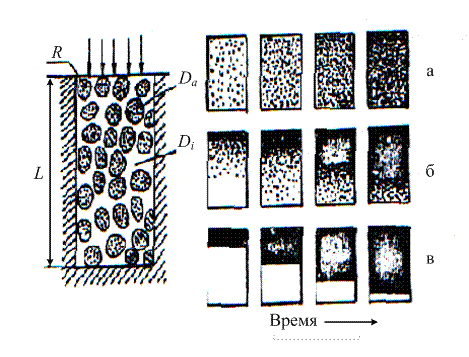
где n = 1, 2, 3,… – ряд целых натуральных чисел; При фиксированном значении степени отработки адсорбционной ёмкости (например, γ = 0,5) уравнение (3.5) упрощается и решается относительно коэффициента D e: где t 0,5 − время полуотработки адсорбционной ёмкости, т.е. промежуток времени, прошедший от начала опыта до того момента, когда количество адсорбированного вещества достигнет 50 % от равновесной величины адсорбции; К – коэффициент, зависящий от формы гранул. Для шара К = 0,308. Для гранул иных форм получены аналогичные значения К. Определенные в ходе опытов значения D и De не вполне корректны. Они получены в предположении, что изотермы адсорбции линейны. Между тем, они, как правило, выпуклы. Адсорбция всегда идет с выделением тепла. Расчёт же коэффициентов диффузии осуществляется в предположении, что процесс адсорбции изотермичен. Но самое главное ─ это непригодность экспериментально измеренных коэффициентов диффузии D и De для прямого прогнозирования переноса в других системах и условиях, чем те, которые были использованы в опытах. Чтобы такое прогнозирование оказалось возможным, необходимы модели структуры адсорбентов и модели переноса вещества в них. Основным экспериментальным материалом о кинетике адсорбции служит кинетическая кривая. Для истолкования кинетической кривой в простейшем случае предполагают, что зерно адсорбента имеет совершенно однородную по объему пористую структуру (эту модель называют квазигомогенной). Значительное усовершенствование квазигомогенной модели – это представление о том, что каждое зерно содержит области с более крупными и более тонкими порами. Диффузия в таком зерне описывается двумя соответствующими коэффициентами. На рис. 3.2 приведена модель бипористого адсорбента, которая служит естественной геометрической моделью гранулированных цеолитов [21]. В первом приближении все поры активных углей также можно разделить на две основные группы – адсорбирующие поры (микро- и супермикропоры) и траспортные поры (мезо- и макропоры). Модель бипористого адсорбента характеризуется двумя коэффициентами диффузии (коэффициенты диффузии в адсорбирующих Da и транспортных Di порах) и двумя значительно различающимися характерными размерами (размер гранул L и радиус микропористых зон R). На рис. 3.2 (справа) приведены результаты изучения кинетики адсорбции рентгеноконтрастного вещества (например, бромбензола из потока азота) методом рентгеновского просвечивания. Если скорость адсорбции контролируется переносом в транспортных порах, на рентгеновском снимке это проявляется в образовании и перемещении по грануле отчётливого адсорбционного фронта (случай в).-
Рис. 3.2. Модель бипористого адсорбента и характер распределения адсорбата в грануле бипористого адсорбента: а – процесс контролируется диффузией в адсорбирующих порах, б – сопротивления массопереносу в адсорбирующих и транспортных порах соизмеримы, в – лимитирующей стадией процесса является перенос в транспортных порах
Во втором предельном случае (а), если процесс контролируется диффузией в адсорбирующих порах, происходит постепенная отработка всей гранулы в целом. В случае (б) образование и распространение по грануле существенно размытого адсорбционного фронта свидетельствует о том, что сопротивления массопереносу в адсорбирующих и транспортных порах соизмеримы.
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.63 (0.01 с.) |

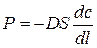 , (3.1)
, (3.1)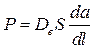 , (3.2)
, (3.2)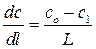 ,
,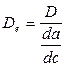
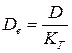 , (3.3)
, (3.3)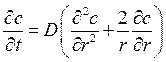 , (3.4)
, (3.4)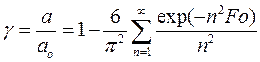 , (3.5)
, (3.5)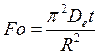 – диффузионный критерий Фурье, R – радиус гранулы.
– диффузионный критерий Фурье, R – радиус гранулы.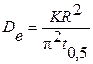 , (3.6)
, (3.6)