
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Константа равновесия реакции ХИОСодержание книги
Поиск на нашем сайте
Прежде всего, отметим, что для изотопологов составляющая суммы по состояниям e эл.одинакова, т.к. электронное строение атомов элементов, занимающих одно место в Периодической системе элементов Д. И. Менделеева одно и то же. Поэтому при определении констант равновесия реакций ХИО нет необходимости в расчете этой составляющей, и сумма по состояниям включает в себя только поступательный, вращательный и колебательный сомножители. При этом, как следует из уравнения (5.23), для расчета константы равновесия необходимо определить отношение сумм по состояниям отличающихся своим изотопным составом изотопологов для каждого из участвующих в реакции веществ. Поступательная энергия молекул и атомов не квантуется, зависит только от их массы и температуры:
Таким образом, для изотопологов при Т=const отношение поступательных составляющих, например, молекул AX и BX, выражается следующим образом:
Вращательная энергия для двухатомной молекулы квантуется и выражается следующим образом:
где Be – вращательная постоянная молекулы Статистический вес данного вращательного уровня зависит от спинов ядер, образующих молекулу, и для каждого уровня существует (2 J +1) разных ориентаций молекулы с одинаковой энергией. Исходя из этого, вращательная сумма по состояниям молекулы может быть выражена следующим образом:
При обычных для реакций изотопного обмена температурах величина интегрирование которого приводит к следующему уравнению:
Для двухатомных молекул реализуется только часть из возможных вращательных состояний, равная 1/ s, поэтому для таких молекул
Для нелинейной многоатомной молекулы, имеющей три вращательные степени свободы и соответствующие им моменты инерции
Отношение вращательных составляющих для изотопологов многоатомного вещества, следовательно, может быть записано в виде уравнения:
Колебательная энергия молекулы так же, как и вращательная, квантуется и, в приближении гармонического осциллятора, может быть записана в следующем виде: Статистический вес каждого колебательного уровня g кол. =1. Вынося за скобки энергию нулевого колебательного уровня, колебательную составляющую суммы по состояниям двухатомной молекулы можно записать в следующем виде: Выражение в скобках представляет собой сумму членов бесконечно убывающей геометрической прогрессии с первым членом, равным 1, и знаменателем прогрессии, равным
В многоатомных молекулах возможны различные типы колебаний – симметричные и антисимметричные валентные, деформационные. Для нелинейной молекулы, состоящей из n атомов, число возможных частот колебания равно 3 n -6 (например, у молекулы воды – 3 частоты), у линейной молекулы число возможных частот равно 3 n -5, однако некоторые из них могут быть вырождены. Например, у линейной молекулы диоксида углерода число экспериментально наблюдаемых частот равно 3, хотя число возможных частот 3х3-5=4. Таким образом, для многоатомных молекул уравнения для колебательной составляющей суммы по состояниям имеют следующий вид:
и Величину
Из уравнения (5.35 – 5.37) видно, что, в отличие от поступательной и вращательной составляющих суммы по состояниям, колебательная составляющая, помимо собственных частот колебания молекул, зависит и от температуры. Проанализируем эту зависимость. При низких температурах, когда величина
Таким образом, все необходимые выражения для составляющих суммы по состояниям молекул изотопологов получены выше. Пользуясь уравнением (5.23), для реакции AX + BY ↔ BX + AY выражение для константы равновесия можно записать в следующем виде:
т.е. для расчета константы равновесия необходимо определить отношение сумм по состоянию для соответствующих изотопологов реагирующих веществ. Используя составные части этой суммы, записанные в виде уравнений (5.25, 5.32, 5.37), получим:
Уравнение (5.40) можно упростить. Для этого воспользуемся теоремой Теллера – Редлиха, в соответствии с которой для многоатомных молекул справедливо следующее равенство: в котором mA и mB – массы обменивающихся изотопов. Рассмотрим справедливость этого соотношения для случая изотопного атома с двухатомной молекулой: AX + B ↔ BX + A, с константой равновесия
В отношение сумм по состоянию для атомов входит только поступательная составляющая, т.е. Отношение сумм по состоянию молекул AX и BX равно:
и Для рассматриваемого случая по теореме Теллера – Редлиха:
Проверим это соотношение. Выше было показано, что:
Отсюда следует, что:
т.е. подтверждается тождество уравнения (5.46). Отсюда следует, что в уравнении (5.45) три первых его члена можно заменить на отношение частот молекул изотопологов:
Таким образом, использование соотношения между массами изотопов, массами молекул, их моментами инерции и частотами колебания позволяет получить уравнение для расчета константы равновесия, в которое входят только частоты колебаний и числа симметрии молекул изотопологов. Для случая изотопного обмена между двухатомными молекулами уравнение приведено ниже: Отметим, что отношение чисел симметрии для этого случая равно 1. Для общего случая изотопного обмена многоатомных молекул в уравнении (5.51) появляются произведения частот и суммы их разности: С использованием уравнений (5.50 – 5.52) рассмотрим влияние температуры на величину К. При высокой температуре разница в нулевых энергиях изотопологов Полученное уравнение является термодинамическим доказательством утверждения, сделанного в разделе 4 при рассмотрении связи между константой равновесия реакции изотопного обмена и коэффициентом разделения в ней.
5.4. Определение коэффициента разделения реакции ХИО с использованием β - факторов Реакцию химического изотопного обмена в общей форме можно записать с помощью следующего уравнения: mAnX + nBmY ↔ mBnX + nAmY. (5.54) В разделе 4 показано, что значение a для этой реакции может быть рассчитано по уравнению (4.21):
В свою очередь, величина константы равновесия при равновероятностном распределении изотопов К ¥ определяется с использованием чисел симметрии реагирующих молекул:
Анализ этого уравнения показывает, что, независимо от конкретных величин чисел симметрии молекул, принимающих участие в реакции (5.54), значение K ¥ для нее равно единице(числа симметрии изотопологов молекул и показатели степени в уравнении для них одинаковы). С учетом этого можно записать следующее уравнение для расчета a в реакции (5.54) с использованием сумм по состояниям: Запись этого уравнения можно упростить, если использовать математическое понятие гиперболического синуса:
Величины, стоящие в числителе и знаменателе уравнения (5.57), Варшавский и Вайсберг назвали β -факторам:
Таким образом, с использованием величин β -факторов запись уравнения для расчета коэффициента разделения упрощается:
а для расчета коэффициента разделения, по-прежнему, необходимы только собственные частоты колебаний реагирующих молекул. В табл.2 приведены величины β –факторов при Т=300 К для ряда практически важных систем, используемых при разделении изотопов водорода. В основе величин, приведенных в таблице, лежат экспериментальные данные о частотах колебаний различных изотопомеров веществ. Использование данных табл. 2 позволяет рассчитать величину коэффициента разделения для любой пары участвующих в изотопном обмене веществ при 300 К. Отметим, что температурные зависимости β -факторов также известны и могут быть найдены в соответствующей литературе. Отметим, однако, что приведенные в таблице величины относятся к веществам, находящимся в одной фазе (газ или пар).
Таблица 2 Значения β -факторов различных изотопологов веществ, участвующих в реакции изотопного обмена. Т=300К
Поэтому при расчете коэффициентов для двухфазных систем (именно такие системы имеют практическое значение) необходимо вносить поправки, природа которых будет обсуждаться ниже в разделе 6.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.37.129 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

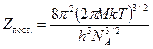 . (5.24)
. (5.24)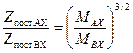 . (5.25)
. (5.25)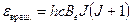 , (5.26)
, (5.26)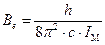 , IM = m . r 2 – момент инерции молекулы при значении ее приведенной массы m и межъядерном расстоянии r, J – вращательное квантовое число.
, IM = m . r 2 – момент инерции молекулы при значении ее приведенной массы m и межъядерном расстоянии r, J – вращательное квантовое число.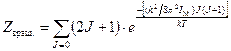 . (5.27)
. (5.27)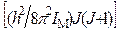 <<kT, и поэтому величину суммы можно заменить интегралом
<<kT, и поэтому величину суммы можно заменить интегралом 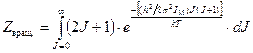 , (5.28)
, (5.28)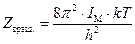 . (5.29)
. (5.29)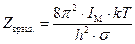 . (5.30)
. (5.30)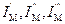 , сумма по состояниям записывается следующим уравнением:
, сумма по состояниям записывается следующим уравнением: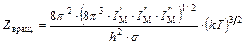 . (5.31)
. (5.31)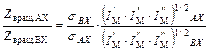 . (5.32)
. (5.32)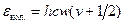 (см. уравнение (2.1)).
(см. уравнение (2.1)).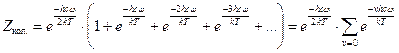 . (5.33)
. (5.33)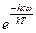 . Тогда:
. Тогда: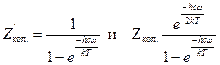 . (5.34)
. (5.34)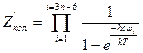 для нелинейной молекулы, (5.35)
для нелинейной молекулы, (5.35)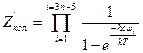 для линейной молекулы. (5.36)
для линейной молекулы. (5.36)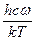 принято называть приведенной температурой U. Используя это обозначение и заменив
принято называть приведенной температурой U. Используя это обозначение и заменив 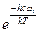 на exp - U, получим для отношения сумм по состояниям многоатомных молекул изотопологов следующее выражение:
на exp - U, получим для отношения сумм по состояниям многоатомных молекул изотопологов следующее выражение: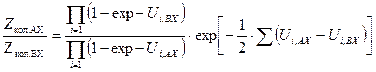 . (5.37)
. (5.37)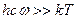 , значение
, значение 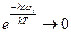 и
и 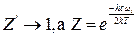 . Наоборот, при высоких температурах
. Наоборот, при высоких температурах 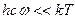 и величину
и величину 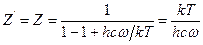 . (5.38)
. (5.38) 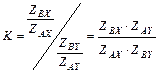 , (5.39)
, (5.39)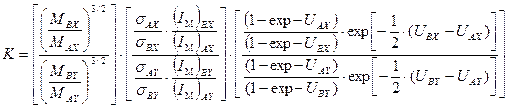 . (5.40)
. (5.40) 
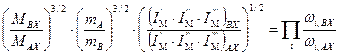 , (5.41)
, (5.41)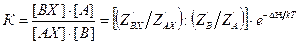 . (5.42)
. (5.42) . (5.43)
. (5.43)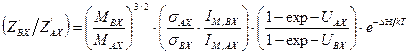 . (5.44)
. (5.44)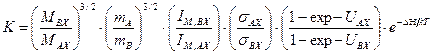 (5.45)
(5.45)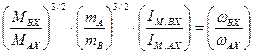 . (5.46)
. (5.46) , (5.47)
, (5.47)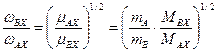 . (5.48)
. (5.48)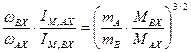 , (5.49)
, (5.49)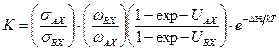 . (5.50)
. (5.50)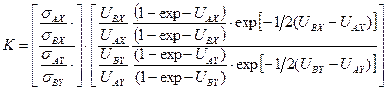 . (5.51)
. (5.51)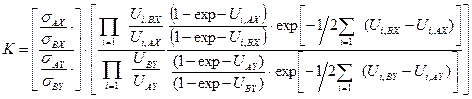 . (5.52)
. (5.52)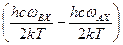 стремится к 0, и, следовательно, величины
стремится к 0, и, следовательно, величины 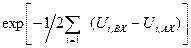 стремятся к 1. Далее, экспонента в знаменателе величины
стремятся к 1. Далее, экспонента в знаменателе величины  вследствие малости значения
вследствие малости значения 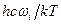 может быть разложена в ряд (см. уравнение 5.38), и, после преобразования, эти члены в уравнениях также равны 1. Это означает, что величина константы равновесия реакции изотопного обмена при стремлении температуры к бесконечности равна отношению чисел симметрии реагирующих молекул, т.е.
может быть разложена в ряд (см. уравнение 5.38), и, после преобразования, эти члены в уравнениях также равны 1. Это означает, что величина константы равновесия реакции изотопного обмена при стремлении температуры к бесконечности равна отношению чисел симметрии реагирующих молекул, т.е.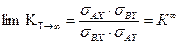 . (5.53)
. (5.53)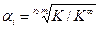 .
. 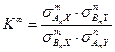 . (5.55)
. (5.55)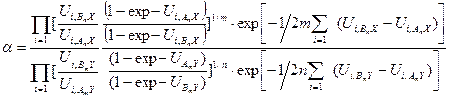 . (5.56)
. (5.56)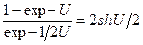 . Тогда уравнение (5.56) можно записать в следующем виде:
. Тогда уравнение (5.56) можно записать в следующем виде: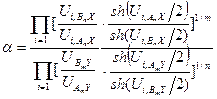 . (5.57)
. (5.57)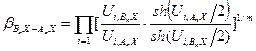 и
и 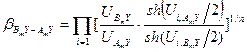 . (5.58)
. (5.58)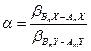 , (5.59)
, (5.59)


