
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация разделительных процессовСодержание книги
Поиск на нашем сайте
Разделительные процессы можно разбить на две группы – необратимые (неравновесные) и обратимые (равновесные). К числу необратимых процессов, используемых для разделения изотопов, относятся центрифугирование, газовая диффузия и термодиффузия, фотохимический и лазерный методы, масс – сепарация и ряд других. Отличительными особенностями этих методов является то, что при умножении однократных разделительных эффектов на каждой ступени процесса разделения необходимо затрачивать энергию, а величина перерабатываемого потока концентрата целевого компонента уменьшается от ступени к ступени разделения. Причиной возникновения изотопных эффектов (превышения значения a над 1) в этих процессах является различие в массах изотопологов, от которых зависят коэффициенты диффузии, величина центробежной силы, сила взаимодействия заряженных частиц с электрическими и магнитными полями и т.д. В силу неравновесности процесса, значения a в каждой ступени разделения зависят от многих факторов, связанных с условиями его осуществления, и могут изменяться от ступени к ступени. Для разделения изотопов легких элементов необратимые процессы разделения не нашли широкого применения. В качестве исключений можно привести два примера. Первые несколько тонн тяжелой воды были получены в начале 40-х годов прошлого века в Норвегии методом многоступенчатого электролиза воды. В последующем при производстве тяжелой воды от этого метода отказались в силу его неэкономичности. На рубеже XX – XXI веков в г. Калининграде (Россия) было запущено промышленное производство изотопа 136С лазерным методом. Приведенными примерами исчерпываются случаи использования необратимых методов для промышленного производства изотопов легких элементов, хотя научные и инженерные работы в этом направлении продолжаются. Простейшим примером обратимых процессов разделения является ректификация. В силу равенства теплоты испарения и конденсации вещества в адиабатических условиях умножение однократного разделительного эффекта не требует дополнительных затрат энергии, а величина потоков по каскаду разделительных элементов остается постоянной. Затраты энергии необходимы только на концах каскада: для рассматриваемого примера – в испарителе для получения потока пара и в конденсаторе для получения потока жидкости. При этом возможны различные варианты рекуперации тепловых потоков.
В рассмотренном примере в процессе участвует одно вещество, находящееся в двух агрегатных состояниях – жидкость и пар. Могут использоваться и другие варианты комбинации различных фазовых состояний вещества – жидкость – твердое тело, газ – твердое тело. Такие процессы называются фазовым изотопным обменом (ФИО). Другая большая группа обратимых методов относится к системам из двух веществ, формально химически не взаимодействующих между собой, т .к. элементный состав исходных веществ и продуктов их взаимодействия не изменяется. Между этими веществами протекает реакция изотопного обмена, в котором вещества обмениваются между собой только изотопами. Эти процессы называются реакциями химического изотопного обмена (ХИО). Обратимые процессы являются равновесными, и причина возникновения изотопных эффектов в них – термодинамическая. Для того, чтобы целевой изотоп концентрировался в каком-либо веществе (в реакции ХИО) или определенной фазе вещества (в процессе ФИО), необходим энергетически выгодный процесс, при протекании которого распределение целевого изотопа в веществах не будет равновероятностным потому, что суммарная свободная энергия его продуктов ниже свободной энергии исходных веществ. Природа этого изотопного эффекта заключается в различии нулевых колебательных уровней различных изотопологов вещества. Колебательная энергия молекулы при использовании модели гармонического осциллятора может быть выражена следующим уравнением:
где h – постоянная Планка, с – скорость света, w – собственная частота колебания молекулы, u – колебательное квантовое число. Для нулевого колебательного уровня
в котором К – силовая постоянная молекулы (для данной молекулы не зависит от изотопного замещения), m – ее приведенная масса молекулы. Для двухатомной молекулы АХ приведенная масса рассчитывается следующим образом:
где mA и mX – массы атомов А и Х соответственно. Рассчитаем отношение приведенных масс двухатомного фрагмента молекулы воды –ОН при различном изотопном замещении – 168О11Н, 168О21Н, 188О11Н. Приведенные массы этих фрагментов равны соответственно 16/17, 32/18 и 18/19. Тогда отношение собственных частот колебаний и, следовательно, энергий нулевых колебательных уровней, для этих фрагментов будут следующими: w 168О11Н/ w 168О21Н= Из проведенного расчета следует важный вывод: обратимые процессы разделения изотопов водорода всегда будут сопровождаться значительно большими изотопными эффектами, чем процессы обмена с участием изотопов других элементов. Поскольку изотопные эффекты в обратимых процессах имеют термодинамическую природу, величины коэффициентов разделения в таких процессах либо совпадают, либо однозначно связаны с константой равновесия реакции ХИО (эта связь будет рассмотрена ниже). Так же, как и любая константа равновесия, коэффициент разделения для данной реакции зависит, в первую очередь, от температуры. Несмотря на то, что изотопные смеси является идеальными[1], при разделении изотопов водорода значения a могут зависеть также от концентрации тяжелого изотопа в смеси. Эта зависимость объясняется изменением изотопологов, преобладающе участвующих в реакции, при изменении концентрации целевого изотопа в реагирующих веществах. Например, в реакции ХИО между водой и водородом при увеличении концентрации дейтерия в реагирующих веществах происходит последовательное изменение формы изотопологов, участвующих в реакции: Н2О®HDO®D2O и H2®HD®D2). Это сопровождается изменением w и энергий нулевого колебательного уровня соответствующих молекул, а значит и различия в этих энергиях. В общем виде уравнения обратимых реакций изотопного обмена можно записать в виде следующих уравнений: - реакции фазового изотопного обмена BnXж(тв) + АBn-1Xп(ж) ↔ ABn-1Xж(тв) + BnXп(ж), (2.4) (например,168О2(ж) + 168O188O(п) ↔ 168О188O(ж) + 168O2(п)), где А и В – разделяемые изотопы элемента (А – целевой изотоп), индексы ж, тв, п обозначают агрегатное состояние вещества (жидкое, твердое, пар), Х – другой элемент или их группа, образующие с данными изотопами рабочее вещество, - реакции химического изотопного обмена BnX + АBn-1Y ↔ ABn-1X + BnY, (2.5) (например, H2O + HDS ↔ HDO + H2S), где X и Y – разные по природе фрагменты изотопологов веществ. Для молекул, имеющих в своем составе несколько атомов изотопов, существует еще один тип реакций изотопного обмена, который называется реакциями гомомолекулярного изотопного обмена (ГМИО): BnXж(тв) + А2Bn-2X ↔ 2ABn-1X, (2.6) (например, NH3 + ND2H ↔ 2NDH2 ). В этих реакциях принимают участие различные изотопологи одного и того же вещества. Такие реакции могут протекать самопроизвольно и быстро, как, например, в аммиаке и воде, а могут для своего осуществления требовать наличия катализатора, как, например, в молекулярном водороде или диоксиде углерода. На примере реакции ГМИО воды покажем подход к расчету мольных концентраций изотопологов при известной атомной доле данного изотопа в ней. Для реакции ГМИО
Н2О + D2O ↔ 2HDO (2.7) константа равновесия равна где величины в квадратных скобках выражены в мольных долях соответствующих изотопологов, причем при любом содержании дейтерия При фиксированном содержании дейтерия в воде его атомную концентрацию можно выразить следующим образом:
При изменении атомной концентрации дейтерия в воде мольные концентрации изотопологов изменяются (рис. 3).
Рис.3. Распределение изотопологов воды при изменения атомной доли дейтерия в ней Из рисунка видно, что в области малых концентраций дейтерия (до 10-15 ат.%) в воде в основном присутствуют два изотополога – Н2О и HDO, а при концентрации дейтерия больше 80 ат.% – HDO и D2O. Преобразуя уравнения (2.8, 2.10) и учитывая уравнение (2.9), можно получить следующее квадратное уравнение:
в котором [D] – концентрация дейтерия в воде, в атомных долях. Решение этого уравнения позволяет определить величину отношения мольных концентраций H2O и HDO и далее, с использованием уравнений (2.8, 2.9), определить мольные концентрации всех изотопологов воды. В заключение этого раздела отметим, что в настоящее время обратимые процессы разделения являются основными при производстве изотопов водорода, лития, бора, углерода, азота, кислорода. Поэтому при дальнейшем изложении материала основное внимание будет уделено именно этим методам.
|
|||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.83.78 (0.012 с.) |

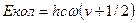 , (2.1)
, (2.1)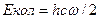 . Собственная частота колебания молекулы выражается следующим уравнением:
. Собственная частота колебания молекулы выражается следующим уравнением: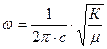 ,
,  (2.2)
(2.2)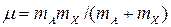 , (2.3)
, (2.3) 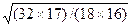 = 1,37, w 168О11Н/ w 188О11Н=
= 1,37, w 168О11Н/ w 188О11Н= 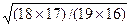 = 1,0033.
= 1,0033.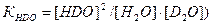 , (2.8)
, (2.8)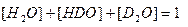 . (2.9)
. (2.9)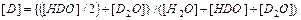 (2.10)
(2.10)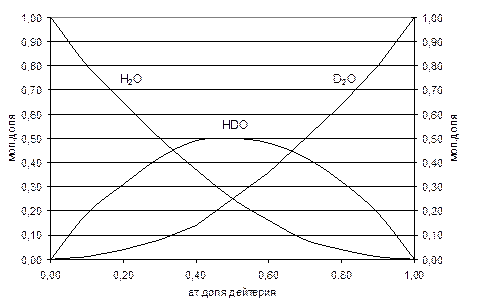
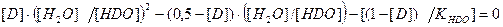 , (2.11)
, (2.11) 


