
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь коэффициента разделения реакции ХИО с константой равновесия реакцииСодержание книги
Поиск на нашем сайте
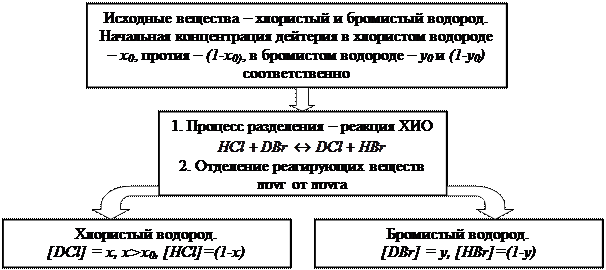
Рассмотрим простейший случай, когда в реакции ХИО принимают участие два вещества, содержащие только по одному обменивающемуся атому изотопа: AX + BY ↔ BX + AY. (4.1) Пример такой реакции: HCl + DBr ↔ DCl +HBr. (4.2) В этой реакции в условиях равновесия дейтерий концентрируется в хлористом водороде, значение a при 298 К равно 1,22. Учитывая, что реакция является обратимой, равновесное распределение дейтерия в ее продуктах не зависит от того, каковы исходные концентрации дейтерия в реагирующих веществах. В предельных случаях может быть полностью дейтерирован хлористый или бромистый водород, однако после их контактирования в системе установится равновесие, и после разделения реагирующих веществ концентрация дейтерия в хлористом водороде будет выше, чем в бромистом. Для случая, когда исходная концентрация дейтерия в хлористом водороде меньше, чем в бромистом, можно привести схему, аналогичную данной на рис. 1 (рис. 5).
Рис.5. Принципиальная схема процесса разделения изотопов водорода по реакции ХИО между хлористым и бромистым водородом С учетом введенных обозначений константу равновесия этой реакции можно записать
т.е. величина константы равновесия совпадает со значением коэффициента разделения. Рассмотрим случай, когда участвующие в реакции ХИО вещества имеют более одного атома обменивающегося изотопа, например 2NH3 + 3D2O ↔ 2ND3 + 3H2O. (4.4) В этой системе имеют место 3 реакции ГМИО: NH3 + NHD2 ↔ 2NH2D, (KNH 2 D) (4.5) NH2D + ND3 ↔ 2NHD2, (KNHD 2) (4.6) H2O + D2O ↔ 2HDO. Обозначим атомную долю дейтерия во всех изотопологах аммиака через x, а в изотопологах воды – через y. Тогда атомная доля протия в этих же веществах равна (1- x) и (1- y) соответственно. При равновероятностном распределении дейтерия по всем изотопологам реагирующих веществ мольную долю каждого из них можно выразить через атомные концентрации изотопов в соответствующих веществах: [ND3]= x3, [NHD2]=3x2(1-x), [NH2D]=3x(1-x)2, [NH3]=(1-x)3, [D2O]=y2, [HDO]=2y(1-y), [H2O]=(1-y)2. (4.8) Коэффициент разделения для реакции (4.4) можно записать следующим образом: Входящие в уравнение (4.9) величины выразим с использованием системы уравнений (4.8)
Алгебраические преобразования уравнения (4.10) приводят к выражению: Аналогичные действия для воды дают следующий результат:
Подставляя уравнения (4.11, 4.12) в уравнение (4.9), получим
Выражение для константы равновесия реакции (4.4) с использованием введенных обозначений будет выглядеть следующим образом:
Полученный результат, однако, является лишь частным случаем. Если, например, рассмотреть реакцию NH3 + 3НDO ↔ ND3 + 3H2O, (4.15) то для нее константа равновесия выражается следующим образом:
Для того, чтобы объяснить появление коэффициента 1/8 в уравнении (4.16), нужно принять во внимание, что при равновероятностном распределении изотопов между изотопологами константа равновесия реакции изотопного обмена равна отношению произведения чисел симметрии (s i) исходных веществ в степенях, равных стехиометрическим коэффициентам, к числам симметрии продуктов реакции в соответствующих степенях. При этом число симметрии молекулы – это количество операций (поворот вокруг оси симметрии на 3600, отражение в плоскости симметрии, инверсия в точке симметрии), в результате которых молекула совмещается сама с собой. Для примера рассмотрим две молекулы – NH3 и NDH2(рис. 6).
Рис. 6. К определению числа симметрии молекул Как видно из приведенного рисунка, число симметрии для молекулы NH 3 равно 3, а для молекулы NH2 D – 1. Таким образом, можно определить значения констант равновесия, например, приведенных выше реакций ГМИО, при условии равновероятностного распределения изотопов (при бесконечно высокой температуре, Ki ¥):
Определим значения константы равновесия K ¥ для реакций (4.4) и (4.15):
Таким образом, коэффициент 1/8, входящий в уравнение (4.16) представляет собой константу равновесия реакции при бесконечно высокой температуре или равновероятностном распределении изотопов, и уравнение (4.15) следует записать в следующем виде:
откуда Величина K ¥ входит и в уравнение (4.14), однако, как показано выше (уравнение (4.17), значение K ¥ для этой реакции равно 1. Обратив внимание на уравнения (4.2, 4.4, 4.15), нетрудно убедиться, что степень корневой зависимости a от отношения констант равновесия соответствующих реакций, равна произведению стехиометрических коэффициентов участвующих в изотопном обмене веществ: 1х1=1 для реакции (4.2), 2х3=6 для реакции (4.4) и 1х3=3 для реакции (4.15). Таким образом, в общем виде уравнение связи коэффициента разделения реакции химического изотопного обмена с константой равновесия реакции можно записать в следующем виде:
Из этого уравнения следует, что в случае, если константа равновесия реакции ХИО равна константе равновесия реакции при равновероятностном распределении изотопов, коэффициент разделения равен 1, т.е. эффект разделения изотопов в такой реакции отсутствует.
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.76 (0.006 с.) |

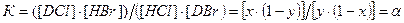 , (4.3)
, (4.3) (KHDO) (4.7)
(KHDO) (4.7)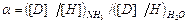 . (4.9)
. (4.9)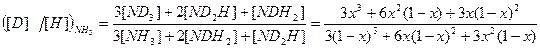 . (4.10)
. (4.10)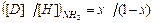 . (4.11)
. (4.11)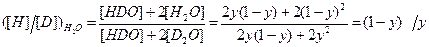 . (4.12)
. (4.12)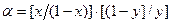 . (4.13)
. (4.13)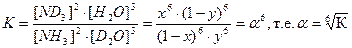 . (4.14)
. (4.14)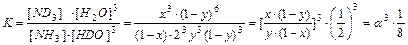 . (4.16)
. (4.16)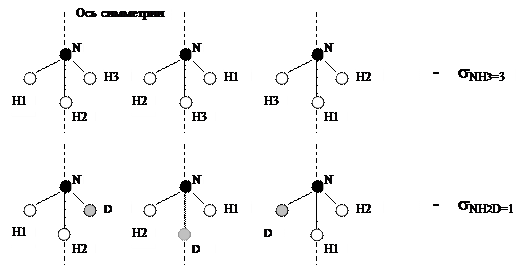
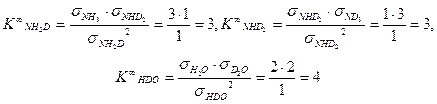
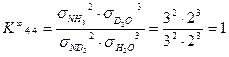 (4.17)
(4.17)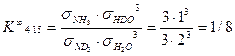 . (4.18)
. (4.18)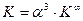 , (4.19)
, (4.19)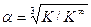 . (4.20)
. (4.20)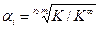 . (4.21)
. (4.21)


