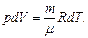Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание установки и порядок выполнения работыСодержание книги
Поиск на нашем сайте
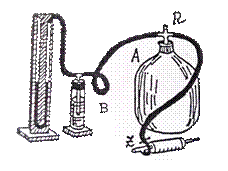
Лабораторная установка состоит из двух калориметров, соединенных металлическим стержнем длиной
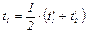 . .
Пусть: Все эти данные, за исключением
Соответственно для коэффициента теплопроводности получаем фор- мулу:
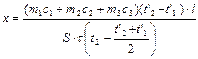 , ,
где
длину стержня l взять 0,115 м. Порядок выполнения работы 1. Калориметры заполняют холодной водой в малый калориметр устанавливают термометр. Воду в большом калориметре доводят до кипе- ния изучают равномерно ли повышается температура в малом калорифере. Для этого изучают насколько поднимается температура за каждые 2 мину- ты. Если изменения температуры за время 2. Из малого калориметра выливают воду и наливают туда 200 мл воды из-под крана, предварительно измерив ее температуру 3. Измеряют время нагревания температуры в малом калориметре на 10 К. 4. По формуле (2.18) определяют значение коэффициента теплопроводности
Контрольные вопросы 1. Чем отличается механизм теплопроводности в твердых телах и в газах? 2. Каков физический смысл теплопроводности? 3. Что общего у всех явлений переноса? 4. Почему зимой металлические предметы кажутся более холодными, чем, например, деревянные?
Лабораторная работа №111 Определение коэффициента поверхностного натяжения жидкости методом отрыва кольца Введение Силы взаимодействия между молекулами в жидкостях играют существенную роль. Силы межмолекулярного притяжения убывают с расстоянием, и уже на сравнительно небольшом удалении молекул друг от друга они практически равны нулю. Если молекула находится внутри жидкости, то вследствие симметрии расположения всех взаимодействующих молекул равнодействующая всех сил, действующих на эту молекулу в радиусе ее молекулярного действия, равна нулю.
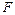 , направленная внутрь жидкости. Переход молекулы из глубины в поверхностный слой связан с необходимостью совершения работы против такой силы. Эта работа идет на увеличение потенциальной энергии молекулы. Поэтому частицы поверхностного слоя обладают большей потенциальной энергией, чем частицы внутри нее. В состоянии устойчивого равновесия система (в нашем случае жидкость) должна иметь минимальное значение потенциальной энергии. Следовательно, жидкость стремится к сокращению своей поверхности, т. е. ведет себя как растянутая упругая пленка. Тенденция к сокращению поверхности жидкости приводит к появлению сил поверхностного натяжения , направленная внутрь жидкости. Переход молекулы из глубины в поверхностный слой связан с необходимостью совершения работы против такой силы. Эта работа идет на увеличение потенциальной энергии молекулы. Поэтому частицы поверхностного слоя обладают большей потенциальной энергией, чем частицы внутри нее. В состоянии устойчивого равновесия система (в нашем случае жидкость) должна иметь минимальное значение потенциальной энергии. Следовательно, жидкость стремится к сокращению своей поверхности, т. е. ведет себя как растянутая упругая пленка. Тенденция к сокращению поверхности жидкости приводит к появлению сил поверхностного натяжения 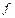 , направленных по касательной к поверхности. Действительно, чтобы удержать "растянутую пленку" в равновесии, нужно по нормали к линии ее границы приложить силу, тем большую, чем больше длина , направленных по касательной к поверхности. Действительно, чтобы удержать "растянутую пленку" в равновесии, нужно по нормали к линии ее границы приложить силу, тем большую, чем больше длина 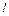 границы пленки: границы пленки:
где Из уравнения (2.19) следует, что коэффициент поверхностного натяжения численно равен силе, действующей на единицу длины контура, ограничивающего рассматриваемую поверхность. В данной работе коэффициент поверхностного натяжения определяется способом отрыва кольца. Если металлическое кольцо погрузить в испытуемую жидкость, то в результате смачивания у краев кольца жидкость поднимается кверху, и силы поверхностного натяжения будут иметь направление, близкое к вертикальному.
где
где Сила, которая удерживает кольцо в жидкости, может быть записана, как Коэффициент поверхностного натяжения (α) может быть записан, как:
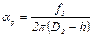 . .
Коэффициент поверхностного натяжения зависит от химического состава жидкости и ее температуры. Измеряется он в Н/м.
Прибор для определения коэффициента поверхностного натяжения жидкости указанным способом состоит из стойки, имеющей вертикальную шкалу (Б), кронштейна (К) и подвешенного на длинной пружине (В) кольца (А). Немного выше плоскости кольца к пружине прикреплена чашечка для грузов и указатель растяжения пружины. К нижней части стойки при помощи винта (М) прикреплён столик (Р), который может перемещаться вдоль стойки в вертикальном направлении. На этот столик помещается сосуд (С) с испытуемой жидкостью.
Порядок выполнения работы 1. Провести калибровку пружины. Для этого убедиться, что плоскость кольца строго горизонтальна. Определить начальное положение пружины X0=0,305 (м) с помощью указателя растяжение по вертикальной шкале. 2. Положить груз m = 2 г на площадку, находящуюся внутри металлического цилиндра, скреплённого с кольцом. Определить по вертикальной шкале удлинение пружины Х =0,315(м). 3. Определить коэффициент жёсткости пружины по формуле:
m – масса положенного груза (кг) g =9.8 м/c2 ускорение свободного падения Гирю из чашечки вынуть. 4. Налить испытуемую жидкость в сосуд, помещённый на подвижный столик. Затем с помощью этого столика, подвести поверхность жидкости к плоскости кольца до их соприкосновения. 5. Медленно, опуская уровень жидкости в сосуде (выпуская жидкость через сливное отверстие), отметить момент отрыва кольца по вертикальной шкале. Результаты записать в таблицу. Измерения провести по 5 раз с чистой и мыльной водой.
6. Определить силу отрыва кольца по формуле:
7. Измерить штангенциркулем наружный диаметр кольца D =0,078 м и толщину кольца h =0,0011 м. 8. Определить коэффициент поверхностного натяжения αp чистой и мыльной воды по формуле (2.22). Коэффициент α зависит от химического состава жидкости и от её температуры. 9. Полученные результаты α p сравнить с αт для обеих жидкостей. 10. Рассчитать погрешности для α p по методу Стьюдента для обеих жидкостей. 11. Обязательно вымыть сосуд после мыльной воды и прочистить сливное отверстие!
Контрольные вопросы 1. По каким причинам возникают силы поверхностного натяжения? 2. Как направлена сила поверхностного натяжения? 3. Почему маленькие капельки дождя равномерно опускающиеся на Землю имеют форму шара? 4. В воздухе плавает мыльный пузырь. Где больше давление газа, внутри пузыря или снаружи?
Лабораторная работа № 113 Определение коэффициента Пуассона Введение Среди всех изопроцессов идеального газа несколько особое место занимает адиабатический процесс. Во-первых, уравнение адиабата нельзя получить непосредственно из основного уравнения газового состояния. Во-вторых, адиабатический процесс происходит без теплообмена с окружающей средой Обсудим условия, при которых процесс может проходить без теплообмена со средой. Их два: – процесс происходит настолько быстро, что заметный теплообмен просто не успевает произойти; – процесс протекает в теплоизолированном от окружающей среды объёме. В качестве примера адиабатического процесса, можно привести процесс распространения звуковой волны. Поскольку скорость распространения волны довольно высока Другим примером является процесс начала истекания воздуха из разорвавшейся камеры автомобиля. Пока давление в камере высоко, велика и скорость истекания и теплообмена не происходит. Выведем уравнение адиабаты. Для этого совместно с уравнением Менделеева–Клапейрона:
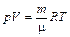 , ,
рассмотрим первое начало термодинамики:

Для адиабатического процесса
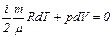 . .
Продифференцируем уравнение Менделеева-Клапейрона:
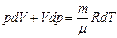 . .
Отсюда получаем:
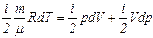 . .
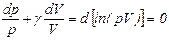
или
Это и есть уравнение адиабаты или уравнение Пуассона. Величина С другой стороны, вспоминая определение теплоемкости
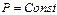 ): ):
Поэтому:
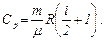 Отсюда следует:
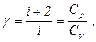
т.е. коэффициент Пуассона показывает, во сколько раз больше тепла следует подвести, чтобы нагревать тело при постоянном давлении, чем при объеме. Коэффициент Пуассона влияет на теоретический верхний предел КПД реально существующих бензиновых двигателей.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.30 (0.014 с.) |

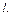 Для устранения возможности теплопередачи через боковую поверхность стержня он обернут слоем теплоизоляции. Калориметр большого диаметра заполняется водой, которая нагревается до температуры кипения
Для устранения возможности теплопередачи через боковую поверхность стержня он обернут слоем теплоизоляции. Калориметр большого диаметра заполняется водой, которая нагревается до температуры кипения 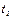 =99,82оС. В калориметр малого диаметра налита холодная вода при температуре
=99,82оС. В калориметр малого диаметра налита холодная вода при температуре 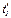 =15оС на 5 градусов ниже комнатной, что достигается при помощи кусочка льда. Температура в малом калориметре начинает повышаться вследствие теплопередачи. Если в течение некоторого времени τ температура
=15оС на 5 градусов ниже комнатной, что достигается при помощи кусочка льда. Температура в малом калориметре начинает повышаться вследствие теплопередачи. Если в течение некоторого времени τ температура 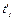 поднимется на 10 градусов до температуры
поднимется на 10 градусов до температуры 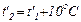 , то можно считать, что переход тепла вдоль стержня происходит так, будто температура холодного конца стержня останется примерно постоянной и равной:
, то можно считать, что переход тепла вдоль стержня происходит так, будто температура холодного конца стержня останется примерно постоянной и равной: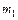 =0,1 кг и
=0,1 кг и 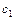 =386,4 Дж/кг*К — соответственно масса и удельная теплоемкость материала калориметра;
=386,4 Дж/кг*К — соответственно масса и удельная теплоемкость материала калориметра; 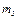 =0,15 кг и
=0,15 кг и 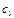 =4200 Дж/кг*К — масса и удельная теплоемкость воды в калориметре;
=4200 Дж/кг*К — масса и удельная теплоемкость воды в калориметре; 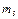 =0,0655 кг и
=0,0655 кг и 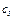 = 386,4Дж/кг*К— масса и удельная теплоёмкость материала стержня.
= 386,4Дж/кг*К— масса и удельная теплоёмкость материала стержня.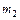 , указаны на установке.
, указаны на установке.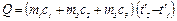 .
.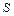 =0,000314
=0,000314 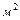 ;
;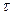 — время нагрева холодного калориметра на 10оС, взять 406 секунд;
— время нагрева холодного калориметра на 10оС, взять 406 секунд;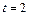 мин на интервалах
мин на интервалах 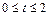 ,
, 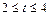 и т. д. происходит на примерно одинаковую величину
и т. д. происходит на примерно одинаковую величину 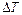 , то тепловой поток можно считать установившемся.
, то тепловой поток можно считать установившемся.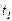 .
.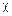 и по методу однократных косвенных измерений определяют погрешность
и по методу однократных косвенных измерений определяют погрешность 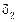 . После этого записывают ответ в виде
. После этого записывают ответ в виде 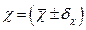 Вт/м
Вт/м  К.
К.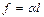 ,
,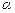 — коэффициент поверхностного натяжения.
— коэффициент поверхностного натяжения.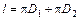 ,
,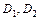 — внутренний и внешний диаметры кольца.
— внутренний и внешний диаметры кольца.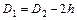 ,
,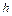 — толщина кольца.
— толщина кольца.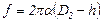 и она равна упругой силе
и она равна упругой силе 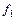 , возникающей в пружине в момент отрыва кольца от жидкости.
, возникающей в пружине в момент отрыва кольца от жидкости.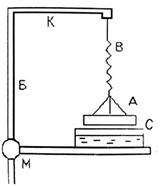 Описание установки
Описание установки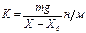
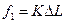 для чистой и мыльной воды, где ∆L – разница между начальным положением пружины X0 и средним значением Lcр взятым из экспериментальной таблицы:
для чистой и мыльной воды, где ∆L – разница между начальным положением пружины X0 и средним значением Lcр взятым из экспериментальной таблицы: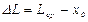 , м
, м
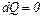 . Поскольку изменение энтропии системы определяется формулой
. Поскольку изменение энтропии системы определяется формулой 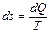 , то ясно, что адиабатический процесс не изменяет энтропию, т. е. этот процесс является изоэнтропийным, а значит и обратим термодинамическим процессом. По этой причине адиабатические процессы занимают весьма важное место в современной энергетике больших мощностей.
, то ясно, что адиабатический процесс не изменяет энтропию, т. е. этот процесс является изоэнтропийным, а значит и обратим термодинамическим процессом. По этой причине адиабатические процессы занимают весьма важное место в современной энергетике больших мощностей.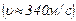 , то обмен энергией между волной и средой просто не успевает произойти.
, то обмен энергией между волной и средой просто не успевает произойти.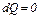 , поэтому:
, поэтому: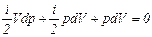 .
.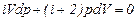 .
.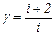 — коэффициент Пуассона, i — число степеней свободы молекулы газа, то из последнего уравнения легко получить:
— коэффициент Пуассона, i — число степеней свободы молекулы газа, то из последнего уравнения легко получить: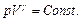
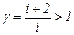 называется показателем адиабаты или коэффициентом Пуассона.
называется показателем адиабаты или коэффициентом Пуассона.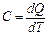 — количество тепла, необходимое для того, чтобы нагреть тело на 1К, сразу находим, что при нагревании при постоянном объеме
— количество тепла, необходимое для того, чтобы нагреть тело на 1К, сразу находим, что при нагревании при постоянном объеме 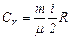 .
.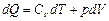 .
.