
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента вязкого трения жидкостиСодержание книги
Поиск на нашем сайте
Цель работы – определить коэффициент вязкости для масла при комнатой температуре по методу Стокса. Свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой называется вязкостью. В то же время, механизм вязкости может оказаться различным для газов и жидкостей. Рассмотрим, например, твёрдое тело, двигающееся в воздухе. В процессе своего движения это тело толкает молекулы воздуха, и происходит ударный обмен импульсами. Тело теряет импульс, а молекулы воздуха, наоборот, приобретают его. Это при- водит к тому, что на тело действует сила вязкого трения:
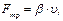
где
Вязкость газа не зависит от его плотности, так как при сжатии газа общее количество молекул, переходящих из слоя в слой увеличивается, но зато каждая молекула менее глубоко проникает в соседний слой. Так как с ростом температуры газа средняя скорость молекул газа растет, то вязкость газов с ростом температуры газа также увеличивается. Теперь рассмотрим ламинарное (без завихрений) течение жидкости по круглому каналу. Эпюра скоростей имеет вид, изображённый на рис. 2.1. Чем больше расстояние от оси трубы, тем меньше скорость. Сравним два кольцевых слоя жидкости, расположенных на расстояниях

Для вязкой жидкости сила внутреннего трения выражается формулой:

где
Коэффициент вязкости зависит от температуры жидкости и с повышением температуры он уменьшается. Поскольку проводить измерения в сплошном потоке очень сложно, в работе используется метод измерения вязкости жидкости, предложенный Стоксом. Наблюдения проводятся не за движением самой жидкости, а за движением маленького круглого шарика в этой жидкости (рис. 2.2.). При движении шарик смачивается окружающей жидкостью и на его поверхности образуется тонкий пограничный слой, двигающийся относительно остальной неподвижной жидкости.
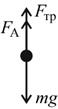
Рассмотрим движение шарика в жидкости. Вниз на него действует сила тяжести
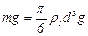
де
где В результате уравнение движения шарика записывается в виде:
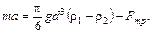
Если шарик падает в жидкость с малой высоты, то после преодоления сил поверхностного натяжения он начинает тонуть с практически нулевой скоростью. При этом сила трения мала и шарик разгоняется. Равновесие наступает при
где
Порядок выполнения работы
 в метрах. в метрах.
2. Бросить один из трех шариков в отверстие крышки на верху колбы с касторовым маслом. 3. Включить секундомер после того, как шарик погрузится в жидкость на 20 см по линейке. Измерить время падения шарика 4. Провести аналогичные действия с остальными шариками. Результаты занести в таблицу 2.2. 5. Рассчитать скорость
где
где
6. Рассчитать среднее значение 7. Записать окончательный результат:
Сравнить с табличным значением 8. Рассчитать число Рейнольдса
где
По Контрольные вопросы 1. Какие явления переноса вы знаете? Что между ними общего? 2. Чем отличается вызванное трение в жидкостях и газах? 3. Какое принципиальное отличие между вязким трением и сухим трением между двумя трущимися поверхностями? 4. Почему результат опыта доказывает, что сила вязкого трения зависит от скорости? 5. В чём состоит метод Стокса определения вязкости жидкости? 6. Каким образом коэффициент вязкости зависит от температуры?
Лабораторная работа № 110
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.106.9 (0.007 с.) |

 — скорость тела;
— скорость тела; — коэффициент пропорциональности.
— коэффициент пропорциональности.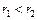 от оси трубы. Поскольку
от оси трубы. Поскольку 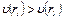 , то относительная скорость
, то относительная скорость  Это приводит к тому, что мимо медленного слоя по ходу движения проходит большее число молекул, т.о. наблюдается некоторый массовый расход жидкости. Относительно быстрого слоя массовый расход жидкости направлен, наоборот, в сторону противоположную движению. Поскольку между молекулами жидкости существуют силы притяжения, то быстрый слой испытывает силу торможения, а медленный слой будет ускоряться. Как видим, для газа механизм передачи импульса – ударный, а для жидкости - бесконтактный, но в обоих случаях зависимость силы трения оказывается линейной.
Это приводит к тому, что мимо медленного слоя по ходу движения проходит большее число молекул, т.о. наблюдается некоторый массовый расход жидкости. Относительно быстрого слоя массовый расход жидкости направлен, наоборот, в сторону противоположную движению. Поскольку между молекулами жидкости существуют силы притяжения, то быстрый слой испытывает силу торможения, а медленный слой будет ускоряться. Как видим, для газа механизм передачи импульса – ударный, а для жидкости - бесконтактный, но в обоих случаях зависимость силы трения оказывается линейной.
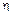 — коэффициент вязкости;
— коэффициент вязкости; — площадь соприкасающихся слоёв;
— площадь соприкасающихся слоёв; — градиент скорости. При движении жидкости по прямой это просто изменение скорости на единицу длины в направлении нормали.
— градиент скорости. При движении жидкости по прямой это просто изменение скорости на единицу длины в направлении нормали.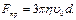
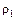 — плотность материала шарика;
— плотность материала шарика;
 — плотность жидкости.
— плотность жидкости.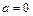 и
и 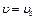 .
.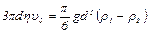 .
.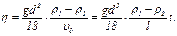
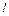 — длина прохождения контрольного участка;
— длина прохождения контрольного участка;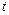 — время прохождения.
— время прохождения.

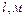

 и коэффициент вязкости
и коэффициент вязкости 
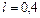 — расстояние, пройденное шариком за время измерения.
— расстояние, пройденное шариком за время измерения.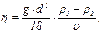
 взять 2030.
взять 2030. ,взять 850.
,взять 850.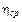 для коэффициента вязкости. Рассчитать абсолютную и относительную погрешность по методу Стьюдента.
для коэффициента вязкости. Рассчитать абсолютную и относительную погрешность по методу Стьюдента.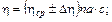

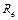 для средних значений υ, d и η:
для средних значений υ, d и η: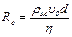 — безразмерная величина,
— безразмерная величина, — плотность касторового масла
— плотность касторового масла 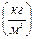 ;
;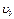 — средняя скорость движения шарика в масле;
— средняя скорость движения шарика в масле;


