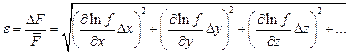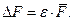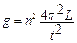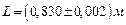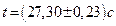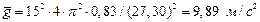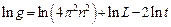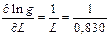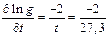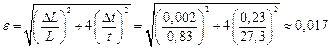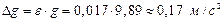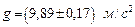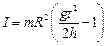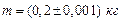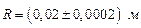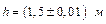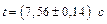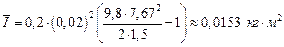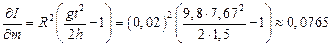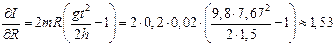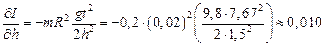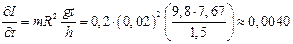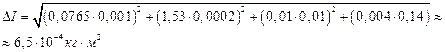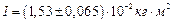Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов многократного прямого измерения при малом числе замеров методом Стьюдента.Содержание книги
Поиск на нашем сайте
Все измерения можно разделить на два вида: прямые и косвенные. Измерение называют прямым, если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора. Измерение называется косвенным, если физическая величина получается в результате вычисления с использованием математической формулы. Нахождение погрешности прямых измерений: 1. Для выбранного числа измерений n измеряемой величины
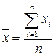
2. Вычисляют стандартное отклонение от среднего значения по формуле:
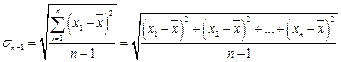
- Для вычисления среднего значения и стандартного отклонения по формулам (1) и (2) можно использовать обычный калькулятор, однако этот способ является время затратным методом. Использование специальных калькуляторов позволяет упростить процедуру вычисления. - При использовании инженерного калькулятора его необходимо перевести в режим вычисления стандартного отклонения (Standard Deviation). Как правило, это делается при помощи последовательного нажатия клавиш Shift+SD, при этом на дисплее индицируется режим «SD». За тем последовательно вводятся значения
- При использовании компьютера с операционной системой Windows необходимо перейти в раздел «Стандартные программы» - для расчета можно использовать утилиты в сети Internet, например: https://ru.numberempire.com/statisticscalculator.php 3. Выбирают доверительную вероятность или надежность
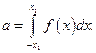
Величина доверительного интервала обычно указывается в Государственных Стандартах (ГОСТ) на проведение различных измерений. При проведении измерений во время лабораторных работ на кафедре физики рекомендуется использование значения 4. По заданной надежности a и проведенному числу измерений Таблица коэффициентов Стьюдента
5. Вычисляют абсолютную ошибку прямого многократного измерения в виде:
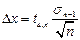
Как видно из (4), погрешность среднего при достаточно больном числе измерений
7. Вычисляется относительная погрешность измерений
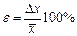
Как видно из формулы (6) относительная погрешность выражается в процентах. Относительную погрешность обычно используют для контроля правильности проведенных измерений. Если
где искомая величина F является функцией одной или нескольких величин x, y, z,… 1. Все величины, которые входят в формулу (7) как аргументы следует записать в форме обработанных результатов прямых измерений:
В целях упрощения надежность величин Для величин являющихся табличными значениями погрешность принимается равной половине последней значащей цифры. 2. Подсчитывается среднее значение величины
3. Вычисляются частные производные функции
4. Рассчитываются численные значения частных производных для средних значений аргументов 5. Находим абсолютную погрешность по формуле:
6. После этого по формуле находят относительную ошибку:
7. Если функция
После этого находят численные значения этих частных производных для значений аргументов, равных:
Затем вычисляется относительная ошибка величины
Из последней формулы можно увидеть, что в этом случае относительная погрешность косвенного измерения определяется суммой относительных погрешностей прямых измерений всех аргументов. Абсолютная погрешность определяется по формуле:
Пример №1. Вычислить ускорение свободного падения g и погрешность D g из измерений длины L физического маятника, совершившего n колебаний за время t:
n =15 Решение:
Пример №2. Определение момента инерции маховика динамическим методом: Решение:
Решение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.009 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

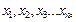 находят среднее арифметическое значение измеряемой величины:
находят среднее арифметическое значение измеряемой величины: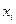 , сопровождаемые нажатием клавиши «DATE», после которого высвечивается номер только что введенного значения
, сопровождаемые нажатием клавиши «DATE», после которого высвечивается номер только что введенного значения 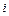 . Вслед за тем как введены все
. Вслед за тем как введены все 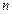 значений, нажатие клавиши «
значений, нажатие клавиши «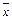 »приводит к индикации среднего значения, а последующее нажатие клавиши «
»приводит к индикации среднего значения, а последующее нажатие клавиши «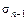 » выводит на дисплей величину стандартного отклонения.
» выводит на дисплей величину стандартного отклонения.
 «Калькулятор» и выбрать режим «Статистика». Последовательно ввести значения
«Калькулятор» и выбрать режим «Статистика». Последовательно ввести значения 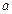 которая обычно лежит в диапазоне
которая обычно лежит в диапазоне 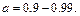
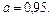
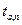 .
.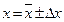
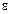 :
: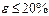 , то можно считать, что измерения проведены правильно, то есть отсутствуют выбросы при проведении измерений и грубые ошибки при вычислениях.
, то можно считать, что измерения проведены правильно, то есть отсутствуют выбросы при проведении измерений и грубые ошибки при вычислениях.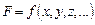
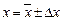
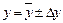
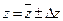
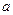 берется для всех величин одинаковой, хотя при необходимости это ограничение может быть снято.
берется для всех величин одинаковой, хотя при необходимости это ограничение может быть снято.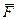 . Для этого в формулу (7) в качестве аргументов подставляются средние значения соответствующих величин:
. Для этого в формулу (7) в качестве аргументов подставляются средние значения соответствующих величин: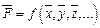
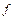 по всем аргументам:
по всем аргументам: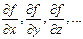
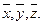
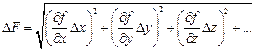 .
.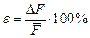
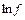 по всем аргументам:
по всем аргументам: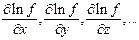
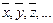
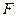 по формуле:
по формуле: