
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Фотоэффект. Эффект Комптона. Фотоны.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Волны де Бройля Основные формулы
Методические указания Гипотеза Планка, что атомные осцилляторы излучают энергию не непрерывно, а определенными порциями - квантами, позволила объяснить явление фотоэффекта. Так как излучение испускается определенными порциями, то энергия осциллятора egможет принимать только определенные дискретные значения, кратные целому числу элементарных порций энергии e0. При решении задач на явления фотоэффекта необходимо выяснить, какой тип фотоэффекта происходит согласно условиям задачи, выбрать соответствующее ему выражение или закон и найти искомую величину. В случае нелинейного (многофотонного) фотоэффекта плотность фотонов в лазерных пучках очень велика, поэтому фотоэлектрон может приобрести энергию, необходимую для выхода из вещества, даже под действием света с частотой, меньшей красной границы при однофотонном фотоэффекте. Таким образом, красная граница нелинейного фотоэффекта смещается в область более длинных волн. Наиболее полно корпускулярные свойства света проявляются в эффекте Комптона. Эффект Комптона - это результат упругого столкновения рентгеновских фотонов со свободными электронами вещества. При решении задач на эффект Комптона необходимо использовать законы сохранения энергии и импульса. Примеры решения задач Пример №1. Электрическая лампа мощностью 100Вт испускает 3% потребляемой энергии в форме видимого света (λ=550 нм) равномерно по всем направлениям. Сколько фотонов видимого света попадает за 1с в зрачок наблюдателя (диаметр зрачка 4 мм), находящегося на расстоянии 10 км от лампы?
N ` γ=0,03·P·t·λ/4·π·r2·h·c. Площадь зрачка наблюдателя Sзр=π·d2/4. Тогда Nγ= N`γ· Sзр =0,03·P·t·λ·π·d2/16·π·r2·h·c. Проверка единицы измерения расчетной величины:Nγ =1=Дж·м2·м·с/м2·Дж·м·с=1 Расчет числового значения:Nз=8,3·104 фотонов. Ответ: Nз=8,3·104фотонов.
Пример №2. Найти постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой υ1 = 2,2·1015, полностью задерживается разностью потенциалов Uз1 = 6.6 В, а вырываемые светом с частотой υ2 = 4,6·1015 Гц разностью потенциалов Uз2 = 16.5 В.
Выразим изАвых: Авых= h·υ1- е·Uз1, и подставим в уравнение Эйнштейна h·υ2 = h·υ1 -е·Uз1+ е·Uз2. Преобразуем так: h·(υ2-υ1) = е·(Uз2-Uз1). И получим: h = e·(Uз1-Uз2)/(υ2- υ1). Проверим единицу измерения: (h) = Дж·с=Кл·В/с-1= Дж·с Расчет: h=1,6·10-19Кл·9,9В/2,4·1015=6,6·10-34Дж·с Ответ: h=6.6·10-34Дж·с. Пример №3. Электрон, начальной скоростью которого можно пренебречь прошел ускоряющую разность потенциалов U=30кВ. Найти длину волны де Бройля.
Е0=m0·c2. Если Тк=<T0, то движение электрона является релятивистским, еслиТк<<T0, то классическим. Т = е·U1 = 1.6·10-19 ·3·104Дж = 4.8·10-15Дж = 3·104 эВ; еU = me ·v2 / 2.
E0 = m0·c2=0.5 МэВ = 5·105эВ Т. к Т<<Е0- имеем дело с классическим случаем движения электрона. Тогда
Расчет числовой величины: λ= 11, 61 10 –25 м. Ответ: λ = 11, 61 * 10 –25 м. Пример №4. Определить максимальную скорость υмах фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ1 = 0,155 мкм; 2) γ – излучением с длиной волны λ2 = 2,47 пм.
Ек = m0υ 2 / 2, или по релятивистской: Ек = (m - m0) с 2. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона во много раз меньше энергии покоя электрона, то может быть применена классическая формула; если же энергия фотона сравнима с энергией покоя электрона то вычисление по классической формуле приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по релятивистской формуле. ε1 = hc / λ1. ε1 = 8 эВ. Это значение энергии фотона много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая: ε1 = А вых + m0υ 2 / 2, откуда:
Расчет: υмах = 1,08 Мм/с. Вычислим энергию фотона γ – излучения: ε2 = hc / λ2 = 8,04 * 10 –15 Дж = 0,502 МэВ. Работа выхода электрона пренебрежимо мала по сравнению с энергией γ – фотона, поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: Ек мах = ε2 = 0,502 МэВ. Так как в данном случае кинетическая энергия электрона сравнима с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии: Ек мах = Е0(1/ где Е0 = m0 с 2, выполнив преобразования получим: β = Следовательно, максимальная скорость фотоэлектронов, вырываемых γ – излучением: υмах = с β = 226 Мм/с. Ответ: 1) υмах = 1,08 Мм/с. 2) υмах = 226 Мм/с. Пример №5. Определить красную границу λ0 фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны λ= 400 нм максимальная скорость фотоэлектронов равна υмах = 0,65 Мм/с?
hc / λ0 = А, отсюда: λ0 = hc / А. Работу выхода для цезия определим с помощью уравнения Эйнштейна: А вых = ε - Ек = hc / λ - m υ 2 / 2 = 3,05 * 10 –19 Дж, тогда: λ0 = 640 нм. Ответ: λ0 = 640 нм. Пример №6. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол θ = 90 0. Энергия ε, рассеянного фотона равна 0,4 МэВ. Определить энергию ε фотона до рассеяния.
преобразуем, с учетом: ε = 2 π ħ с / λ, а длины волн λ, и λ выразим через энергии ε, и ε соответствующих фотонов: 2 π ħ с / ε, - 2 π ħ с / ε = (2 π ħ с/ m с2) 2 sin2 θ/2 ε = (ε, m с2 ) / m с2 - ε, 2 sin2 θ/2 = ε, Е0 / Е0 – 2 ε,sin2 θ/2, где Е0 = m0 с 2 Расчет: ε = 1,85 МэВ. Ответ: ε = 1,85 МэВ. Пример №7. Параллельный пучок света длиной волны λ = 500 нм падает нормально на зачерненную поверхность, производя давление р = 10 мкПа. Определить: 1) концентрацию фотонов n в пучке; 2) число фотонов n1, падающих на поверхность площадью 1 м2 за время 1 с.
ω = p / (1 + ρ). И получим: n = p / (1 + ρ) ε. Энергия фотона зависит от частоты, а следовательно и от длины световой волны: ε = hυ = hc / λ. Получим искомую концентрацию фотонов: n = p λ / (1 + ρ) hc. Коэффициент отражения ρ для зачерненной поверхности принимаем равным нулю. Расчет: n = 2,52 * 10 13 м–3. Число фотонов n1, падающих на поверхность площадью 1 м2 за время 1 с, найдем из соотношения n1 = N / St, где N – число фотонов, падающих за время t на поверхность площадью S. Но N = ncSt, следовательно, n1 = ncSt / St = nc Расчет: n1 = 7, 56 * 10 21 м–2 с –1 Ответ: n = 2,52 * 10 13 м–3, n1 = 7, 56 * 10 21 м–2 с –1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.93 (0.011 с.) |

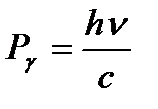 ,
,
 , где с = 3·108 м/с – скорость распространения света в вакууме.
, где с = 3·108 м/с – скорость распространения света в вакууме.
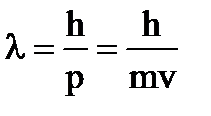 , если v<<c
, если v<<c
 ,
, 
 , где АВЫХ – работа выхода электрона из металла,me = 9,1·10-31 кг – масса электрона, N –число фотонов, одновременно передающих энергию электрону, испускаемому металлом (N=2
, где АВЫХ – работа выхода электрона из металла,me = 9,1·10-31 кг – масса электрона, N –число фотонов, одновременно передающих энергию электрону, испускаемому металлом (N=2  .
.
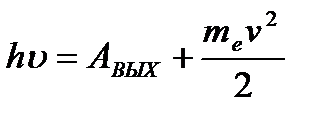 ,. где АВЫХ – работа выхода электрона из металла,me = 9,1·10-31 кг – масса электрона.
,. где АВЫХ – работа выхода электрона из металла,me = 9,1·10-31 кг – масса электрона.
 .
.
 .
.
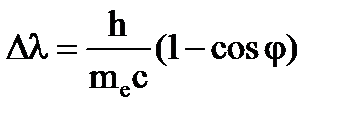 ,
где φ – угол рассеивания электрона.
,
где φ – угол рассеивания электрона.

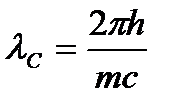 ,гдеm- масса электрона, с- скорость света в вакууме.
,гдеm- масса электрона, с- скорость света в вакууме.
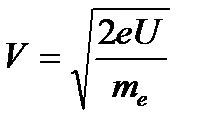 .
.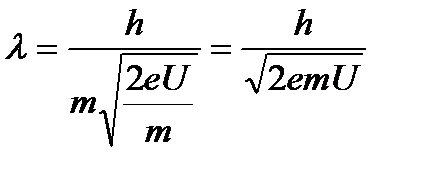 .
. .
.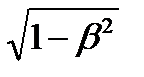 – 1),
– 1),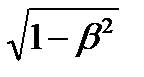 (2 Е0 + Ек мах) Ек мах / (Е0 + Ек мах) = 0,755
(2 Е0 + Ек мах) Ек мах / (Е0 + Ек мах) = 0,755


