
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение эмпирических функциональных зависимостейСодержание книги
Поиск на нашем сайте и их параметров
Целью измерения может являться установление вида функциональной зависимости между измеряемыми неодноименными величинами. Если величина у зависит от величины х, то для определения вида этой зависимости необходимо одновременно измерять как значения x i, так и соответствующие им значения y i. Совместная обработка всех полученных значений x i, y i позволяет найти эмпирическую формулу y = f(x), описывающую искомую зависимость. Существуют различные методы вывода эмпирических формул. Согласно простейшему из них экспериментальные точки xi, yi наносят на график, затем визуально оценивают, можно ли провести какую- либо линию L (прямую, параболу и т.д.) так, чтобы точки xi, yi компактно группировались относительно нее (рис. 5). Выбрав соответствующую линию L, делают выводы о виде функции f (х). Если экспериментальные точки расположены вдоль некоторой прямой L (рис. 6), то аппроксимирующая функция f (х) выбирается в виде y = а 0 + а 1 x. (16) Для определения параметров а 0 и а 1 выбирают на прямой L две точки М1 (x 1, y 1) и М2 (x 2, y 2) и составляют два уравнения у 1 = а 0 + а 1 x 1 , у 2 = а 0 + а 1 x 2 , (17) из которых следует: а 0 =
Величины а 0 и а 1 можно определить графически, находя точки пересечения x 0, y 0 прямой L с координатными осями. Тогда а 0 = y 0 , а 1 = - у 0 / х 0. (19) Очевидно, что а 1 - угловой коэффициент графика функции (16). Значения параметров а 0, а 1, … а n с учетом распределения погрешностей измерений могут быть получены методом наименьших квадратов (МНК), в котором используется условие минимума суммы квадратов отклонений Во многих случаях экспериментальные точки хi,yi не располагаются вблизи прямой в координатной системе (х, у). Тогда вид аппроксимирующей функции f (х) устанавливают с помощью замены переменных v = v (x, y), u = u (x, y), (20) выбирая подходящие функции. Если на графике в системе координат (u, v) экспериментальные точки v i = j (x i, y i), ui = y (x i, y i) группируются вдоль прямой линии v = а 0 + а 1 u, (21) то, определив по формулам вида (18), (19) значения параметров а 0 и а 1, можно с помощью формул (20) найти вид f (х). Например, для проверки того, описывается ли исследуемая зависимость степенной функцией вида у = с х b , (22) следует прологарифмировать данную функцию: ln y = ln с + b ln x. Полученное уравнение есть уравнение прямой в координатах ln y, ln x, поэтому проверка выбора аппроксимирующей функции состоит в логарифмировании экспериментальных значений xi, yi и построении графика в осях ln y, ln x (Рис.7).
Если экспериментальные точки на данном графике удовлетворительно группируются относительно прямой линии, то функция (22) может быть принята в качестве аппроксимирующей. Тогда в соответствии с (16)- (18) и (22) можно найти значения параметров b и c:
Проверка соответствия показательной функции у = с e b x (23) экспериментальным данным заключается в построении графика в полулогарифмическом масштабе, так как в координатах ln у, x она образует прямую ln y = ln с + b x. Если построенный график достаточно точно отображает прямую линию, то функция (23) описывает наблюдаемую зависимость у от x (Рис.8). Выбор аппроксимирующей функции - задача неформализуемая, так как одна и та же кривая на данном отрезке с одинаковой точностью может быть описана различными аналитическими выражениями. Поэтому рациональный выбор той или иной функции основан на учете определенных требований, основными из которых являются достаточная простота математического выражения и его содержательность. Содержательность полученной формулы заключается в возможности придания ее параметрам определенного физического смысла. Параметры b и c находятся по формулам
В условиях физического практикума, как правило, производится сопоставление результатов эксперимента с известной теоретической зависимостью, описывающей изучаемое явление. В этом случае теоретическая зависимость выступает в роли аппроксимирующей функции f, и задача сводится к определению по данным эксперимента значений ее параметров и сопоставлению полученных результатов с выводами теории. Например, при изучении свободного падения тела на основании данных о координатах тела уi в определенные моменты времени ti аппроксимирующей функцией является зависимость у = g t 2 / 2, которая в координатах v = y, u = t 2 переходит в линейную зависимость v = (g /2) u. Если на графике экспериментальные точки vi = yi, ui = ti 2 расположены вблизи прямой v = а 1 u, то аппроксимирующая зависимость у = g t 2 / 2 представляется удовлетворительной. Тогда, определив по графику значение параметра а 1 , можно вычислить ускорение свободного падения g = 2 а 1. При изучении процесса разрядки конденсатора по результатам измерения заряда конденсатора qi в определенные моменты времени ti аппроксимирующей функцией является предсказываемая теорией зависимость q (t) = q 0 e - t / t, (24) где q 0 - заряд конденсатора в момент t = 0, t - время релаксации, причем t = R С, R – сопротивление цепи разряда, С - емкость конденсатора. В соответствии с (24) ln q = ln q 0 - t / t, ln q 0 = а 0, - 1/t = а 1. Если на графике экспериментальные точки ln q i, t i располагаются вдоль прямой, то можно полагать, что аппроксимирующая зависимость (24) является удовлетворительной. Тогда, определив по графику значения а 0 и а 1, можно вычислить величину q 0 и время релаксации t.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |
|||||||||||||||||

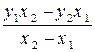 , а 1 =
, а 1 = 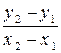 =
= 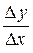 . (18)
. (18)
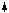

 y
L
x
y
L
x
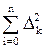 =
= 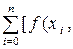 а 0, а 1, … а n ) - y i ]2 = min.
а 0, а 1, … а n ) - y i ]2 = min.
 у
х
у
х
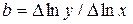 , с = у 1 /
, с = у 1 / 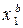 = у 2 /
= у 2 / 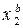 .
.

 у
х
у
х



