Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение законов фотоэффектаСодержание книги
Поиск на нашем сайте
Цель работы: Изучение законов внешнего фотоэффекта и ознакомление с работой фотоэлемента. Приборы принадлежности: Сурьмяно-цезиевый вакуумный фотоэлемент СЦВ-4, оптическая скамья, лампа накаливания, вольтметр, гальванометр, потенциометр (собраны в виде установки).
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
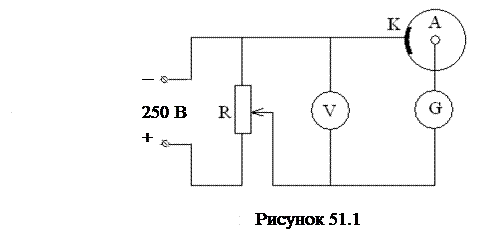
Испускание электронов твердым (или жидким) телом под действием электромагнитного излучения называется фотоэлектронной эмиссией, внешним фотоэлектрическим эффектом или просто фотоэффектом. Согласно уравнению Эйнштейна для внешнего фотоэффекта в металлах W = h ν – A, (51.1) где W - энергия фотоэлектрона, А - работа выхода электрона из металла, h ν - энергия кванта излучения частотой ν, h = 6, 62∙10– 34 Дж . с - постоянная Планка. Из (51.1) следует, что фотоэффект возможен при условии ν ≥ ν0 = А / h. (51.2) Минимальная частота ν0 и соответствующая ей длина волны λ0 = с / ν0 = h с / А, (51.3) где с = 3∙10 8 м/с - скорость света, определяет длинноволновую (красную) границу фотоэффекта. Если каждый фотоэлектрон получает свою энергию только у одного фотона, то число фотоэлектронов должно быть пропорционально числу поглощенных фотонов, т.е. пропорционально интенсивности света. При этом в соответствии с (51.1) энергия фотоэлектрона линейно зависит от частоты и не зависит от интенсивности (числа фотонов). При больших интенсивностях света становится заметной вероятность поглощения одним электроном нескольких фотонов. В этом случае W = n h ν – A, n > 1 (51.4) и строго определенной красной границы не существует. Выводы, полученные на основе уравнения (51.1), подтверждают установленные опытным путем закономерности внешнего фотоэффекта: 1. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота ν0, при которой еще возможен фотоэффект. 2. Максимальная энергия фотоэлектронов линейно растет с частотой излучения и не зависит от его интенсивности. 3. При фиксированной частоте излучения число электронов, выбиваемых из катода в единицу времени, прямо пропорционально интенсивности света. Для изучения закономерностей внешнего фотоэффекта используется фотоэлемент, включенный в цепь источника напряжения (Рис.51.1). Излучение, попадающее на катод, вызывает фотоэмиссию. Испущенные катодом электроны под действием электрического поля направляются к аноду, обеспечивая ток в цепи.
Существование фототока в области отрицательных значений U - от 0 до – U 0 объясняется тем, что фотоэлектроны, выбитые светом из катода, обладают отличной от нуля начальной кинетической Рисунок 51.2 энергией W к. За счет уменьшения этой энергии электроны могут совершать работу против сил задерживающего электрического поля и достигать анода: W к = е U 0, (51.5) где е = 1,6 ∙10 -19 Кл - абсолютное значение заряда электрона. При U ≤ – U 0 фототок I = 0. С увеличением U все большее число электронов достигает анода, т.е. фототок возрастает. Предельное значение силы тока I н называется фототоком насыщения и соответствует таким значениям U, при которых практически все электроны, вылетевшие из катода, попадают на анод. В соответствии с законами фотоэффекта фототок насыщения пропорционален световому потоку Ф, падающему на катод: I н = γФ, (51.6) где γ - интегральная чувствительность фотоэлемента. Световой поток связан с освещенностью катода E площадью S зависимостью Ф = Е S, (51.7) Величина Е выражается через силу света лампы J, принимаемой за точечный источник: Е = J / r 2 , (51.8) где r - расстояние от лампы до фотокатода. Таким образом, I н = γ J S / r 2 . (51.9) В настоящей работе исследуются особенности вольтамперной характеристики фотоэлемента, а также проверяется соотношение (51.9).
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ
В работе исследуется вакуумный фотоэлемент с сурьмяно-цезиевым катодом (СЦВ-4). Схема установки представлена на рис.51.1. Вакуумный фотоэлемент находится в кожухе с окном и освещается осветителем, лампочка которого питается током через понижающий трансформатор. Выпрямитель является источником постоянного напряжения, подаваемого на фотоэлемент. Для снятия вольтамперной характеристики схему включены гальванометр, вольтметр и потенциометр, с помощью которого можно изменять напряжения на фотоэлементе. При снятии световой характеристики - зависимости фототока от величины светового потока изменение величины Ф обеспечивается изменением расстояния между осветителем и фотоэлементом путем перемещения фотоэлемента вдоль оптической скамьи. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание I. Снятие вольтамперной характеристики фотоэлемента. 1.Устанавливают фотоэлемент на расстоянии 25 см от осветителя, открывают окно кожуха фотоэлемента и включают выпрямитель. Переключатель "предел измерения" гальванометра должен стоять в положении 10 мкА. 2. Изменяют с помощью потенциометра напряжение на фотоэлементе от 0 до 30 В с интервалами 5 В и от 30 до 150 В с интервалами 10 В, фиксируя ток с помощью гальванометра. Данные измерений записывают в таблицу 1. 3. Увеличивают расстояние до 45 см и снимают вторую вольтамперную характеристику (см.п.2). Задание 2. Снятие световой характеристики фотоэлемента. 1. Подают на фотоэлемент напряжение 150 В и, изменяя расстояние между фотоэлементом и источником от 25 см до 65 см через 5 см, измеряют фототок насыщения для каждого положения фотоэлемента. Напряжение на фотоэлементе в течение опыта поддерживается постоянным. Яркость лампочки устанавливают максимальной (с помощью тумблера). Данные измерений записывают в таблицу 2. 2. Уменьшают напряжение на фотоэлементе до 100 В и, установив яркость лампочки минимальной, снимают вторую световую характеристику.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. По данным таблицы 1 строят вольтамперные характеристики (на одном рисунке). 2. По данным таблицы 2 строят на одном рисунке две световые характеристики фотоэлемента.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Будет ли наблюдаться фотоэффект у лития (А =2,39 эВ) при освещении светом длиной волны l=400 нм? 2. При освещении металла светом с длиной волны l задерживающий потенциал для фотоэлектронов оказался равным U з. Найти работу выхода электронов из данного металла. 3. Чему равна максимальная скорость фотоэлектронов, вырванных с поверхности платины излучением с длиной волны l? 4. Определить плотность тока насыщения фотокатода, освещаемого излучением с длиной волны l, энергетической освещенностью Е, если 4% падающих фотонов выбивают один электрон. 5. Ток насыщения вакуумного фотоэлемента I н. Определить число фотоэлектронов, покидающих поверхность катода в единицу времени. 6.
Лабораторная работа № 52
ВНЕШНИЙ ФОТОЭФФЕКТ
Цель работы: Ознакомление с закономерностями внешнего фотоэффекта, определение красной границы и работы выхода материала фотокатода. Приборы и принадлежности: Компьютерная модель
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Испускание электронов телом под действием электромагнитного излучения называется фотоэлектронной эмиссией, внешним фотоэлектрическим эффектом или просто фотоэффектом. Согласно уравнению Эйнштейна для внешнего фотоэффекта в металлах W = h ν – A, (52.1) где W - энергия фотоэлектрона, А - работа выхода электрона из металла, h ν - энергия кванта излучения частотой ν, h = 6, 62∙10– 34 Дж . с - постоянная Планка. Из (52.1) следует, что фотоэффект возможен при условии ν ≥ ν0 = А / h. (52.2) Минимальная частота ν0 и соответствующая ей длина волны λ0 = с / ν0 = h с / А, (52.3) где с = 3∙10 8 м/с - скорость света, определяет длинноволновую (красную) границу фотоэффекта. Если каждый фотоэлектрон получает свою энергию только у одного фотона, то число фотоэлектронов должно быть пропорционально числу поглощенных фотонов, т.е. пропорционально интенсивности света. При этом в соответствии с (52.1) энергия фотоэлектрона линейно зависит от частоты и не зависит от интенсивности (числа фотонов). При больших интенсивностях света становится заметной вероятность поглощения одним электроном нескольких фотонов. В этом случае W = n h ν – A, n > 1 (52.4) и строго определенной красной границы не существует. Выводы, полученные на основе уравнения (52.1), подтверждают установленные опытным путем закономерности внешнего фотоэффекта: 1. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота ν0, при которой еще возможен фотоэффект. 2. Максимальная энергия фотоэлектронов линейно растет с частотой излучения и не зависит от его интенсивности. 3. При фиксированной частоте излучения число электронов, выбиваемых из катода в единицу времени, прямо пропорционально интенсивности света.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для начала работы необходимо дважды щелкнуть левой кнопкой мыши, расположив ее маркер над эмблемой сборника компьютерных моделей. Затем - дважды щелкнуть левой кнопкой мыши, установив ее маркер над названием раздела Квантовая физика. Установить маркер мыши над надписью компьютерной модели Фотоэффект и дважды коротко щелкнуть левой кнопкой мыши. После этого появляется рабочее окно. (Для закрытия окна надо нажать на кнопку с крестом в верхнем правом углу данного окна). Установка заданных значений интенсивности (мощности) Р и длины волны излучения l а также напряжения U производится с помощью соответствующих линеек выбора перемещением маркера по линейке или нажатием кнопки-стрелки (для дискретного изменения параметра). 1. Исследование зависимости величины фототока I от анодного напряжения U: а) устанавливают значение длины волны l < 600 нм; б) устанавливают значение мощности Р1 = 1,0 мВт; в) увеличивая напряжение в интервале от –1,2 В В до 3,0 В через г) устанавливают значение мощности Р2 = 0,5 мВт и повторяют измерения п. в). Результаты измерений заносят в таблицу 1. 2. Исследование зависимости величины фототока насыщения I н от мощности изучения Р: а) устанавливают значение длины волны l1 в интервале (380-450) нм; б) устанавливают значение напряжения U = 3,0 В; в) увеличивая значение P от нуля до 1,0 Вт с шагом D Р = 0,1 Вт, находят соответствующие значения фототока; г) измерения п.п. б), в) проводят при значениях l2 l3. Результаты измерений заносят в таблицу 2. 3. Исследование зависимости запирающего напряжения от длины волны падающего излучения: а) устанавливают заданное значение мощности Р =1,0 мВт; б) устанавливают минимально допустимое значение l. Изменяют величину напряжения U, отмечают, при каком значении U фототок прекращается. Записывают это значение. в) повторяют измерения п.б), последовательно увеличивая величину l с шагом 10 нм. Установленные значения l и найденные значения запирающего напряжения U З заносят в таблицу 3.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 1. По результатам измерений строят графики зависимости фототока I от анодного напряжения U для двух значений мощности P. 2. По результатам измерений строят графики зависимости фототока I от мощности P для трех значений длины волны l. 3. По результатам измерений и вычислений строят график зависимости модуля запирающего напряжения U З от обратной длины волны (106/l) падающего излучения. Находят угловой коэффициент к графика зависимости ç U З ç= f (106/l): к =D ç U З ç/D(106/l) а также отрезок а, отсекаемый графиком на оси (106/l). Постоянная Планка и красная граница и работа выхода материала фотокатода находятся по формулам:
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ 1. При облучении фотокатода светом с l1 максимальная кинетическая энергия фотоэлектронов W 1. Какова максимальная кинетическая энергия фотоэлектронов при облучении этого же фотокатода светом с l2? 2. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница l0, а максимальная кинетическая энергия фотоэлектрона W? 3. Определить красную границу фотоэффекта, если работа выхода электрона из металла А. 4. 5.
Лабораторная работа №53
ИЗУЧЕНИЕ СПЕКТРА ВОДОРОДА Цель работы: Экспериментальное определение длины волны трех линий серии Бальмера и вычисление постоянной Ридберга. Приборы и принадлежности: Спектрометр-монохроматор УМ-2, оптическая скамья, источники излучения.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
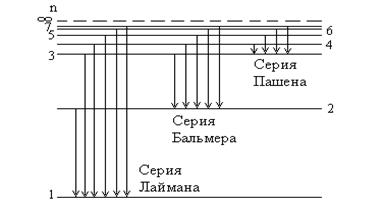
Если свет от раскаленного тела пропустить через призму, то на экране за нею наблюдается картина, называемая спектром испускания. Раскаленные твердые и жидкие тела и газы (под высоким давлением) дают сплошной спектр, в котором спектральные цвета непрерывно переходят от одного к другому. Спектр нагретых разреженных газов и паров является линейчатым, т.е. состоит из отдельных цветных линий. Молекулы испускают полосатые спектры. Каждый химический элемент имеет типичный для него линейчатый спектр. Для анализа спектров применяют, например, спектроскоп, служащий для пространственного разделения лучей различных длин волн (наблюдение спектра производится визуально). При переходе атома из одного начального стационарного состояния с энергией Е n в другое конечное состояние с энергией Е m (Е m < En) происходит излучение кванта света h n = En - Е m, (53.1) где h = 6,62 × 10-34 Дж × с - постоянная Планка, n - частота испускаемого монохроматического излучения. Установлено, что линии в спектрах атома расположены не беспорядочно, а объединяются в группы или серии. Отчетливее всего это обнаруживается в спектре простейшего атома - водорода. В спектре водорода имеется несколько серий: серия Лаймана в крайней ультрафиолетовой области, серия Бальмера в видимой и близкой ультрафиолетовой области, серии Пашена, Брэкета и Пфунда в инфракрасной области спектра. Часть линий серии Бальмера лежит в видимой области спектра и доступна визуальному наблюдению. Первые четыре линии серии Бальмера обозначают символами Н a, Н b, Н g и Н d. Длины волн спектральных линий водорода, принадлежащих к серии Бальмера, удовлетворяют формуле
где R - постоянная Ридберга, n =3,4,5,... Все сериальные формулы спектра водорода могут быть выражены единой формулой где m и n - целые числа, причем для каждой серии n = m +1, m +2, m +3 и т.д. Для серии Лаймана m = 1, для серии Бальмера m = 2, для серии Пашена m = 3 и т.д. На рис.53.1 схематически показаны уровни энергии стационарных состояний электрона в атоме водорода. Состояние атома с наименьшей энергией (n =1) называется основным. Атом, получивший некоторую энергию и перешедший из нормального основного состояния в возбужденное, через
Рисунок 53.1 малое время (порядка 10-8 с) может возвратиться в исходное состояние, теряя энергию h n на излучение света частоты n, соответствующей длине волны l= с /n. Переход атома из возбужденного состояния может происходить не только в основное состояние, но и в промежуточные энергетические состояния. Этим объясняется происхождение ряда спектральных серий: если m постоянно, а n принимает ряд последовательных целочисленных значений, то возникают линии одной и той же серии. На рис. 53.1 различные энергетические переходы схематически изображены вертикальными линиями.
ОПИСАНИЕ АППАРАТУРЫ
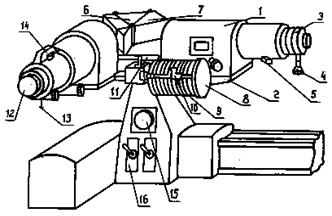
Оптика призменного спектрометра УМ-2 состоит из коллиматора, диспергирующей призмы с поворотным механизмом, зрительной трубы. Назначение коллиматора - дать параллельный пучок света, падающий на диспергирующую призму (рис.53.2). Коллиматор крепится в обойме 1 на плато 2. В качестве выходной щели коллиматора применена стандартная симметричная щель 3, ширина раскрытия щели от 0 до 4 мм, высота - 15 мм, цена деления на барабанчике 4 равна 0,01 мм. В трубе коллиматора между щелью и объективом помещен затвор, с помощью которого можно прекратить доступ света в прибор. Движением затвора управляют с помощью рукоятки 5.
Рисунок 53.2 Столик 6, на котором установлена призма 7, с помощью рычага получает движение от микрометрического винта 8. На барабане длин волн 9 поворотного механизма нанесены относительные деления - градусы. Цена каждого деления - 2о. Отсчет читается против индекса 10, скользящего по спиральной канавке. Во время работы шкала и индекс освещаются лампочкой 11. Лучи света, пройдя диспергирующую призму, попадают в окуляр зрительной трубы 12. В фокальной плоскости окуляра зрительной трубы имеется указатель с головкой 13, освещаемой лампочкой через сменные светофильтры в револьверной оправе 14; таким образом, при работе в любой области спектра указатель может быть освещен светом в этой же области длин волн. Для регулировки освещения указателя на приборе установлен реостат 15 с выключателем 16. Источником света служит разрядная трубка, наполненная водородом. От специального блока питания на нее подается регулируемое высокое напряжение. Для градуировки используется излучение ртутной лампы, питаемой от пульта ЭПС-115 и постоянно закрепленной на оптической скамье. Между источником света и спектрометром находится собирающая линза - конденсор, концентрирующая свет на входной щели спектрометра. Пульт ЭПС-115 служит для питания ртутной лампы и осветительной системы спектрометра. Тумблеры, расположенные на основании прибора, позволяют включать лампочки осветителей шкал и указателя спектральных линий. Яркость освещения указателя регулируется реостатом.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Включают в сеть пульт питания и тумблер ДРШ, нажимают пусковую кнопку ПК ртутной лампы и дают ей прогреться в течение 4-5 минут. Включают тумблеры подсветки шкалы и указателя. 2. Вращая барабан 9, наблюдают в окуляр 12 спектральные линии ртути. Для отсчета положения спектральной линии ее центр совмещают с острием указателя. Фокусируют прибор на резкость изображения. Сначала устанавливают зрительную трубу окуляра 12 так, чтобы изображение острия указателя было резким. Затем получают четкое изображение спектральных линий при помощи микрометрического винта 17. 3. Фиксируют показания шкалы барабана N, соответствующие спектральным линиям ртути l. Для правильной индентификации линий сопоставляют наблюдаемую картину со стандартным спектром ртути, прилагаемым к установке. Данные измерений N заносят в таблицу 1. 4. Измерения проводят для всех линий ртутного спектра, указанных в таблице 1. 5. По окончании измерений ртутную лампу выключают. 6. Ставят на оптическую скамью водородную трубку, включают блок питания и устанавливают такое напряжение, при котором начинается устойчивый разряд. В красной части спектра водорода находят интенсивную линию Ha, вторая линия Hb - зелено-голубая. Третья линия - фиолетовая. Этой линии предшествуют две слабые и размазанные молекулярные фиолетовые полосы. Рассмотрев спектр водорода и установив, какие именно линии этого спектра являются H a, H b, H g, приступают к измерениям: отмечают деления барабана, соответствующие каждой линии. Данные заносят в таблицу 2. Закончив измерения, немедленно выключают блок питания. Таблица 1 Спектр ртути
Таблица 2 Спектр водорода
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 1. По данным таблицы 1 строят градуировочную кривую спектрометра l= F (N). 2. По графику (градуировки) определяют длины волн линий водорода la, lb и lg. 3. Для найденных значений l и соответствующих им n =3,4,5 вычисляют по формуле (53.2) постоянную Ридберга, находят ее среднее значение и погрешность измерений D R (как для прямых измерений). 4. Записывают окончательный результат в виде R =< R >± D R. 5. Сравнивают результаты опыта с табличным значением R.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ 1. Сколько различных спектральных линий будут излучать атомы водорода после перехода их из основного состояния (n =1) в состояние с большей энергией (m)? 2. Чему равен потенциал ионизации атома водорода, находящегося в состоянии с главным квантовым числом n? 3. Чему равна энергия фотона e, испускаемого при излучении атомом водорода самой длинноволновой линии серии Пашена? 4. Какое физическое явление лежит в основе действия спектральных приборов типа УМ-2? 5. Какой области спектра принадлежат спектральные линии бальмеровской серии Ha, Hb и Hg? 6. Чему равна энергия фотона e, испускаемого при излучении атомом водорода самой длинноволновой линии серии Брекета (m =4)?
Лабораторная работа №54
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.009 с.) |

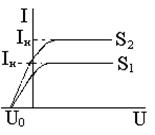 На рис.51.2. представлены вольтамперные характеристики I = f (U) фотоэлемента - зависимости фототока I от напряжения U на фотоэлементе при постоянной интенсивности падающего излучения неизменного спектрального состава. Зависимости соответствуют двум различным освещенностям катода: 1 - при Е1 и 2 - при Е2 > Е1.
На рис.51.2. представлены вольтамперные характеристики I = f (U) фотоэлемента - зависимости фототока I от напряжения U на фотоэлементе при постоянной интенсивности падающего излучения неизменного спектрального состава. Зависимости соответствуют двум различным освещенностям катода: 1 - при Е1 и 2 - при Е2 > Е1. 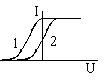 Два фотокатода освещаются одним и тем же источником света. Какой график зависимости I (U) соответствует фотокатоду с меньшей работой выхода?
Два фотокатода освещаются одним и тем же источником света. Какой график зависимости I (U) соответствует фотокатоду с меньшей работой выхода?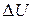 = 0,2В, находят соответствующие значения фототока;
= 0,2В, находят соответствующие значения фототока;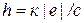 , l0 = 1/ a, А = hc а.
, l0 = 1/ a, А = hc а.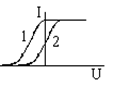 Зависимость фототока от напряжения между катодом и анодом для различных источников монохроматического излучения приведена на рисунке. Какой график соответствует излучению с большей частотой?
Зависимость фототока от напряжения между катодом и анодом для различных источников монохроматического излучения приведена на рисунке. Какой график соответствует излучению с большей частотой?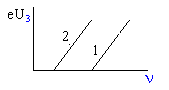 Зависимость задерживающей разности потенциалов от частоты излучения, падающего на два фотокатода приведена на рисунке. Какой график соответствует фотокатоду с большей работой выхода?
Зависимость задерживающей разности потенциалов от частоты излучения, падающего на два фотокатода приведена на рисунке. Какой график соответствует фотокатоду с большей работой выхода?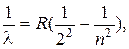 (53.2)
(53.2)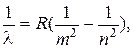 (53.3)
(53.3)