
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов измерений. Лабораторный практикум является неотъемлемой частью курсов Физика и ОсновыСодержание книги
Поиск на нашем сайте
Введение
Лабораторный практикум является неотъемлемой частью курсов "Физика" и "Основы оптики". Работа в лаборатории дает возможность воспроизводить и анализировать основные физические явления, а также способствует развитию практических навыков. Лабораторные работы выполняются студентами в соответствии со следующим порядком: 1. При работе в лаборатории студент обязан выполнять правила техники безопасности, с которыми он знакомится на вводном занятии. 2. При подготовке к выполнению лабораторных работ необходимо изучить описание предстоящей лабораторной работы, ознакомиться по учебной литературе с новыми понятиями и рассматриваемыми в данной работе закономерностями. Придя на занятие, студент должен иметь заготовленную в соответствии с установленным образцом форму отчета. 3. Проверка подготовленности студента и допуск к выполнению очередной лабораторной работы осуществляется преподавателем, ведущим занятие в подгруппе. 4. Перед выполнением работы следует изучить установку и приобрести навыки работы на ней. При обнаружении неисправности установки необходимо сообщить о ней преподавателю. 5. Результаты измерений записываются студентом в своем отчете. После проведения необходимых измерений и вычислений в конце занятия студент представляет отчет на подпись преподавателю. Отчет, не подписанный преподавателем, считается недействительным. Полностью оформленный отчет по выполненной работе представляется на следующем занятии. 6. Каждую выполненную работу студент должен защитить в сроки, указанные в графике. При подготовке к защите работ необходимо просмотреть соответствующий теоретический материал курса по учебнику (или конспекту лекций), а также все вопросы, связанные с выполнением работ - по описаниям лабораторных работ. 7. При защите работы студент должен показать знание теории и методов измерения, используемых в работе; уметь анализировать полученные результаты.
Общие сведения об измерениях
Работа в лабораториях физического практикума - неотъемлемая часть процесса изучения законов и методов физики. Основными задачами физического практикума являются: 1. Обеспечение возможности наблюдения физических явлений. 2. Ознакомление с приборами и методами измерения физических величин. 3. Развитие навыков экспериментального исследования и умения анализировать результаты проведенного эксперимента. Всякий физический эксперимент сводится к нахождению численных значений величин, отображающих свойства изучаемого объекта, находящегося в определенных условиях. Нахождение значений определенной величины опытным путем с помощью специальных технических средств называют измерением. Сущность любого измерения заключается в сравнении измеряемой величины с другой однотипной величиной - эталоном и представление результата этого сравнения в виде числа. В принципе для каждой величины необходим свой эталон. Однако на практике выбирают небольшое число физических величин, эталоны которых принимаются за основные единицы измерения. Единицы измерения всех остальных величин устанавливают по основным, используя физические законы, связывающие эти величины. Совокупность единиц измерения, базирующихся на определенном наборе основных единиц, называется системой единиц. В настоящее время как правило используется Международная система единиц (СИ), основными единицами которой являются: единица длины - метр, массы – килограмм, времени – секунда, силы электрического тока - Ампер, температуры – Кельвин, силы света – кандела, количество вещества – моль. В систему СИ входят также и производные единицы, определяемые через основные единицы на основании физических законов (см. Приложение 1). Вместе с тем допускается применение внесистемных единиц (по отношению к СИ): массы - тонна, центнер; времени - час, минута; плоского угла - градус, минута, секунда и т.д. Все измерения можно классифицировать по различным признакам. В зависимости от числа измерений различают однократные и многократные измерения. При однократном измерении величина измеряется один раз, при многократном - несколько раз. В зависимости от способа получения результата различают прямые и косвенные измерения. Прямые измерения – измерения, при которых искомое значение измеряемой величины определяется непосредственнос помощью соответствующего измерительного средства (измерение длины линейкой, длительности процесса секундомером, температуры термометром и т.п.). Косвенные измерения – определение значения измеряемой величины на основании результатов прямых измерений других величин, функционально связанных с искомой величиной. При этом значение искомой величины находят расчетным путем. Например, значение объема тела находят по характерным размерам тела, значение плотности тока - по результатам измерений силы тока и размеров, характеризующих поперечное сечение проводника и т.п.). Совместные измерения представляют собой проводимые одновременно (прямые или косвенные) измерения нескольких различных величин для определения зависимости между ними. Например, характер зависимости сопротивления проводника от температуры определяется по результатам измерений сопротивления проводника при различных температурах. По виду измеряемой величины различают линейные, механические, тепловые, электрические и другие измерения. Выбор вида измерений и способа обработки их результатов определяется особенностями изучаемого объекта, требованиями к точности результата измерений, оперативности получения информации и т.д.
Средства измерений
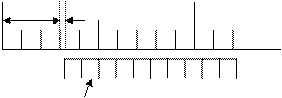
Средством измерения называют техническое устройство, предназначенное для измерений, воспроизводящее и (или) сохраняющее единицу физической величины. К средствам измерений относят меры, измерительные преобразователи, измерительные приборы, измерительные установки и системы. Мера – средство измерений, воспроизводящее физическую величину заданного размера (гири, линейки, измерительные резисторы). Измерительные преобразователи - устройства, преобразующие сигналы измерительной информации в форму, целесообразную для обработки и хранения (термопары, фотоэлементы, датчики давления и т.д.). Измерительные приборы - средства измерения, преобразующие сигналы измерительной информации в форму, доступную для непосредственного восприятия. Все измерительные приборы имеют отсчетные устройства - шкалы и указатели или цифровые индикаторы. Измерительные установки представляют собой совокупность взаимосвязанных средств измерений и других устройств, расположенных в одном месте. Все средства измерений имеют общие свойства, позволяющие сопоставлять их между собой. Погрешность средства измерения определяется как разность между показаниями средства измерения и действительным значением измеряемой величины. Чувствительность - отношение значения изменения выходного сигнала средства измерения к вызывающему его изменению измеряемой величины. Например, чувствительность прибора со стрелочным указателем определяется как отношение угла поворота стрелки Da к соответствующему значению измеряемой величины D х: S = Da /D х. Цена деления шкалы равна числу единиц измеряемой величины, приходящихся на одно наименьшее деление шкалы прибора. Диапазон измерений - область значений измеряемой величины, в которой определены допустимые пределы погрешности данного средства измерений. Границы диапазона измерений являются нижним и верхним пределами измерения. Отсчет по прибору, имеющему шкалу, отградуированную в единицах (или долях) измеряемой величины, представляет собой измерение расстояния между определенными делениями шкалы. Для отсчета долей деления применяются различные приспособления, в частности нониусы. Нониус представляет собой дополнительную шкалу, которая перемещается при измерении вдоль основной шкалы прибора. Простейший нониус - десятичный нониус, представляющий собой линейку, разбитую на 10 равных делений. Длина такого нониуса равна 9 целым делениям основного масштаба (Рис.1). Цена деления основной шкалы А у = 1мм, цена деления нониуса В - 0,1 мм. Нониусы такого типа используются в штангенциркулях.
При положении нониуса, изображенного на рис.2, длина измеряемого отрезка l складывается из 3 делений основной шкалы А (т. е. 3 мм) и отрезка D l, длина которого равна расстоянию от третьего деления основной шкалы до нуля нониуса В. Из рисунка следует, что второй штрих нониуса точно совпадает со штрихом основной шкалы. Таким образом, l = 3,2 мм. Следовательно, при отсчете по нониусу необходимо определить число целых делений основной шкалы прибора, за которое переместился нулевой штрих нониуса, и прибавить к этому числу произведение цены деления нониуса на номер деления нониуса, совпадающего с каким-либо делением основной шкалы. В приборах, предназначенных для измерения углов (угломеров, гониометров) используются круговые нониусы (Рис.3). В ряде приборов доли масштабов отсчитываются по специальной шкале, указатель которой связан с перемещением измерительного устройства. Составной частью многих приборов является микрометрический винт с закрепленным на нем отсчетным барабаном.
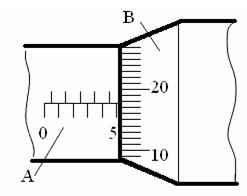
шкале, а число сотых долей миллиметра по шкале барабана. Показания микрометра на рис. 4 составляет 5,18 мм.
Погрешности измерений
Качество средств и результатов измерений характеризуют указанием их погрешностей. Понятие погрешности связано с понятием истинного значения Хист физической величины Х, которое идеальным образом отражает соответствующее свойство изучаемого объекта. Истинное значение всегда неизвестно и не может быть найдено в конкретном, сколь угодно точном эксперименте. Измерение сводится к оценке истинного значения измеряемой величины и установлению степени ее неопределенности, характеризуемой погрешностью. Методы решения этой задачи зависят от вида измерений. Абсолютной погрешностью измерения называют разность между измеренным и истинным значением физической величины, выраженную в единицах измеряемой величины D х = х - Хист. (1) Относительной погрешностью измерений называют отношение абсолютной погрешности измерений к истинному значению измеряемой величины Относительная погрешность служит оценкой качества измерений и обычно выражается в процентах. Погрешность измерения зависит от множества разнообразных факторов, источниками которых являются: - недостатки выбранной модели изучаемого объекта, особенности метода измерения, неточности расчетных формул и т.п. Подобные причины вызывают так называемые методические погрешности; - несовершенствоиспользуемых средств измерений, приводящее к инструментальным (приборным) погрешностям. - считывание показаний прибора, приводящее к погрешностям отсчета, вследствие невозможности точного определения положения указателя прибора и представления результата измерения конечным числом цифр; - математическая обработка результатов измерений, приводящая к вычислительным погрешностям, так как все вычисления ведутся с приближенными числами; - индивидуальные особенности экспериментатора, приводящие к субъективным погрешностям; - неконтролируемые изменения свойств внешней среды, исследуемого объекта, условий проведения эксперимента. По характеру проявления различают систематические, случайные а также грубые погрешности (промахи). Промахи – грубые погрешности, связанные с неправильными действиями экспериментатора, неисправностями аппаратуры или резкими изменениями условий эксперимента. Предполагаемые промахи выявляются на основании определенных критериев и исключаются из рассмотрения. Систематические погрешности – погрешности, остающиеся постоянными или изменяющиеся по определенному закону при многократных измерениях одной и той же величины. Методические, приборные и субъективные погрешности во многих случаях носят систематический характер. Поэтому для выявления и оценки систематических погрешностей необходимы исследования методики и условий эксперимента, поверка приборов, проведение дополнительных измерений и т.д. Обнаружение причин и свойств систематических погрешностей позволяет уменьшить ее, совершенствуя методику эксперимента, применяя более точные приборы, вводя поправки в результат измерений. Часть систематической погрешности остается неустраненной и представляет собой систематическую составляющую D хс погрешности результата измерения. Случайные погрешности - погрешности, величина и знак которых непредсказуемы. Случайные погрешности вызываются множеством неконтролируемых факторов и обнаруживаются при многократных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Полностью устранить случайные погрешности невозможно, их можно только уменьшить путем увеличения числа измерений. Оценка случайных погрешностей D хсл проводится с помощью методов математической статистики. Многократные измерения некоторой величины Х при заданных условиях приводят к набору значений х 1, х 2, … хn, образующих случайную выборку из всех возможных значений х. Оценкой истинного значения измеряемой величины является выборочное среднее (среднее арифметическое) Рассеяние значений хi относительно среднего < x > характеризуется дисперсией DX или средним квадратичным отклонением s х измеряемой величины
Величины < x > и DX являются случайными, так как представляют функции случайных значений хi. Неоднократное повторение измерений и вычисление соответствующих значений приводит к набору значений < x > i. Рассеяние значений <x>i характеризуется средним квадратичным отклонением среднего (стандартным отклонением среднего) Так как истинное значение отличается от среднего значения, то следует рассматривать интервал Число a, определяющее вероятность попадания истинного значения величины Х в интервал где t a n - коэффициент Стьюдента, зависящий от n и a (см. Приложение). В разных областях знаний используют различные значения надежности. Для условий физического практикума достаточно использовать значения a в интервале 0,8 £ a £ 0,95. Появление случайной погрешности, большей 3s - достаточно маловероятное событие. Если погрешность результата превышает значение 3s, его можно считать промахом. Деление погрешностей на систематические и случайные является приемом, используемым для анализа погрешностей. В действительности это составляющие погрешности результата измерений D х, проявляющиеся совместно. Инструментальные погрешности Погрешность средства измерения - характеристика данного средства, определенная при его испытаниях и указанная в его документации. Погрешности средств измерений обусловлены недостаточной точностью образцовых средств, использованных при градуировке, погрешностями регулировки, условиями эксплуатации, изменением со временем свойств отдельных элементов устройства и т.д. Цифровым приборам присуща погрешность квантования (погрешность дискретности), связанная с преобразованием измеряемой величины в цифровой код. Для характеристики большинства средств измерений используют нормированные значения погрешности, являющиеся предельными для данного типа приборов. Обобщенная характеристика, определяющая гарантированные границы значений погрешности а также другие свойства, влияющие на точность, называется классом точности средства измерения. Электроизмерительные приборы характеризуют приведенной погреш-ностью, равной выраженному в процентах отношению абсолютной погрешности к нормирующему значению хн g = (D хпр / хн) 100%. (7) В качестве хн может быть верхний предел измерения, длина шкалы и т.д. Для приборов, допустимые погрешности которых выражаются приведенной погрешностью, классом точности называется приведенная погрешность, выраженная в процентах и совпадающая с числовым значение предела допустимой основной погрешности. Класс точности указывается на шкале прибора или в технической документации. Для аналоговых электромеханических приборов установлены следующие классы точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0; 6,0. Классы точности цифровых измерительных приборов - 0,005; 0,01; 0,02; 0,05; 0,1; 0,2; 0,5; 1,0. Знание класса точности позволяет оценить погрешность измерения физической величины. Класс точности 2,5 означает, что для данного прибора предельная основная относительная погрешность не превышает 2,5 %. Если измерение напряжения производится вольтметром со шкалой 0 - 150 В класса точности 2,5, то на любой отметке шкалы прибора основная абсолютная погрешность не превосходит по модулю величины D x пр = (g × xпред)/ 100%= 2,5×150/ 100 = 3,8 В. Максимальная основная абсолютная погрешность прибора постоянна, поэтому относительная погрешность измерения зависит от показаний прибора. При измерении напряжений U 1 = 20 В и U 2 =100 В максимальные относительные погрешности измерений составят e1 = (D x пр / U 1)100% = 19 %, e2 = (D x пр / U 2)100% = 3,8 % Чем ближе измеренное значение к пределу измерений, тем меньше относительная погрешность. Поэтому рекомендуется использовать приборы так, чтобы измеренное значение составляло 50-90 % от предела измерений. В случае, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления. В частности при измерении линейкой, цена наименьшего деления которой 1 мм, погрешность принимается равной 0,5 мм. Для приборов, оснащенных нониусом, за приборную погрешность принимается цена деления нониуса (для штангенциркуля - 0,1 мм, 0,05мм или 0,02 мм; для микрометра - 0,01 мм). Основная погрешность секундомера равна цене деления. Кроме того, необходим учет погрешности отсчета, определяемой скоростью реакции на включение и выключение прибора. При ручном запуске и остановке прибора погрешность отсчета составляет ~ 0,2 с.
Лабораторная работа № 40 С ПОМОЩЬЮ БИПРИЗМЫ ФРЕНЕЛЯ Цель работы: Определение длины волны излучения с помощью бипризмы Френеля. Приборы и принадлежности: оптическая скамья, осветитель с ртутной лампой, светофильтры, бипризма Френеля, окулярный микрометр с опак-иллюминатором, собирающая линза.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Для наблюдения интерференции света применяют разделение светового пучка, идущего от источника излучения, на два пучка, заставляя их снова встретиться после прохождения ими оптических путей разной длины и проинтерферировать. Так, в схеме с бипризмой Френеля для разделения исходной световой волны используют двойную призму (бипризму) с малым преломляющим углом q.
В результате образуется две когерентные волны, как бы исходящие из мнимых источников S 1 и S 2, лежащих в одной плоскости со щелью S. В области Р Q, где эти волны перекрываются – её называют зоной интерференции – возникает система чередующихся максимумов и минимумов освещённости, которую можно наблюдать на экране. Подсчитаем оптическую разность хода D лучей, исходящих из мнимых источников S 1 и S 2 и приходящих в точку М. В треугольниках S 1 S 2 С и МСО углы a равные и малые, поэтому и Тогда Пусть в точке М наблюдается максимум m – го порядка, тогда Отсюда координата m – го максимума При переходе к соседнему максимуму m меняется на единицу и х – на величину Из формул (41.1), (41.2) и (41.6) легко получить где d – расстояние между мнимыми источниками S 1 и S 2, При наблюдении в белом свете центральный (нулевой) максимум получается белым, остальные окрашенными, поскольку Максимальное число N возможных полос интерференции на экране, где ширина зоны интерференции L = b 2ε, определяется условием N = L / Из формулы (41.6) вытекает соотношение, с помощью которого можно оценить преломляющий угол бипризмы θ (в радианах), считая показатель преломления стекла бипризмы n = 1,50 Предполагалось, что источник света монохроматичен и имеет вид бесконечно узкой щели. Конечность ширины щели приводит к уменьшению резкости интерференционной картины на экране из-за перекрытия элементарных интерференционных картин, возникающих от разных элементов щели. Картина остается резкой, если ширина щели настолько мала, что сдвиг элементарных интерференционных картин от её крайних точек не превысит половины полосы Δ х. Из-за немонохроматичности света полосы постепенно размываются по мере их удаления от центрального максимума. Пусть спектр излучения лежит в интервале Δ λ с = λ в – λ н, где λ н и λ в – длины волн, соответствующих нижней и верхней границам этого интервала. Полосы исчезнут совсем, когда максимум (m + 1) – го порядка для λ н совпадает с максимумом m – го порядка для λ в, т.е. (m + 1) λ н = m λ в. Отсюда наибольшее значение порядка наблюдаемого максимума
Таким образом, чем менее монохроматичен свет, тем более низкие порядки интерференции доступны наблюдению. При достаточной ширине зоны интерференции число наблюдаемых максимумов определяется конечностью ширины спектрального интервала Δ λ с, которую можно оценить. Используя длину волны Если наблюдаемое в окулярный микрометр общее количество полос равно N = 2 m +1, то
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЯ
окулярный микрометр 7 с опак-иллюминатором 6. Интерференционная картина наблюдается в фокальной плоскости окуляра. В поле зрения окулярного микрометра имеется неподвижная шкала с миллиметровыми делениями, перекрестие из двух визирных нитей и связанный с ними указатель в виде двойной черты. Фокусировка на перекрестие и указатель осуществляется перемещением передней линзы окулярного микрометра. При вращении микрометрического винта перекрестие перемещается параллельно шкале. С помощью указателя по шкале определяется положение перекрестия визирных нитей в поле зрения окулярного микрометра. Доли миллиметра отсчитываются по шкале барабана микрометрического винта. Цена деления барабана микрометра 0,01 мм. По ширине l нескольких (k = 8 - 10) полос, можно определить ширину одной полосы Δ x = l / k. (41.13)
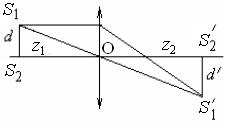
окулярного микрометра и измеряют расстояние между этими изображениями d ¢. Как видно из рис. 41.3,
где z 1и z 2 - расстояния от щели до линзы и от линзы до окулярного микрометра, измеренные по шкале оптической скамьи. С учетом (41.14) формула (41.7) принимает вид
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Все приборы (кроме линзы 5) размещены в соответствии с рис.41.2 на оптической скамье и отцентрированы по высоте. 1. С помощью окулярного микрометра наблюдают интерференционные полосы и определяют их максимальное число N. 2. Измеряют ширину l области, занимаемой k интерференционными полосами. Для этого подводят перекрестие визирных нитей окулярного микрометра на середину одной из светлых полос, расположенных в левой части поля зрения. Делают отсчет х 1 по окулярному микрометру (целые миллиметры по неподвижной шкале, сотые доли по барабану микрометрического винта). Затем, перемещая перекрестие вправо и отсчитав число k пройденных светлых полос, определяют х 2 и l = х 2 х 1. 3. Устанавливают между бипризмой и окулярным микрометром, закрепленными на оптической скамье, вспомогательную линзу 5. Включают подсветку опак-иллюминатора. Не изменяя положения бипризмы и микрометра, перемещают линзу, добиваясь резких изображений двух мнимых источников S 1 и S2 в поле зрения окулярного микрометра. Окулярным микрометром определяют положения х S1 и х S2 мнимых источников S 1 и S 2 и находят d ¢ = х S2 х S1. Измеряют расстояния z 1 между щелью и линзой и z 2 между линзой и окулярным микрометром. 4. Снимают вспомогательную линзу с оптической скамьи, смещают перекрестие визирных нитей окулярного микрометра в новое положение и повторяют измерения (пп.1-3) еще два раза. 5. В третьем опыте измеряют расстояния: а – от щели до бипризмы и b – от бипризмыдо микрометра. 6. Заменяют светофильтр и повторяют измерения (пп.1-5).
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. Результаты всех измерений и расчетов заносят в таблицу 2. Рассчитывают значения λ по формуле (41.14) для каждого опыта. 3. Находят среднее значение <λ > для каждого светофильтра. 4. Находят границы доверительного интервала Dl для длины волны каждого светофильтра по формулам для прямых многократных измерений. 5. Окончательные результаты записывают в виде λ=(<λ>± Dl) мкм. 6. Вычисляют величину спектрального интервала Dlс по формуле (41.12).
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Определить порядок m наблюдаемого на экране максимума, если оптическая разность хода лучей (длина волны l) от мнимых источников равна D. 2. Расстояние между двумя когерентными источниками света (длина волны l) равно d. Расстояние между интерференционными максимумами в средней части интерференционной картины равно D. Определить расстояние L от источников до экрана. 3. Две интерферирующие волны приходят в некоторую точку с разностью хода 2,5l. Усиление или ослабление света будет в этой точке? Источники испускают когерентные световые волны. 4. Какой длины l 2 путь пройдет фронт волны монохроматического света в вакууме за то же время, за какое он проходит путь длиной l 1 в некоторой среде? Показатель преломления среды n 1. 5. Найти ширину зоны интерференции L на экране в опыте с бипризмой Френеля, если расстояние от светящейся щели до бипризмы а, расстояние от бипризмы до экрана b, ширина интерференционной полосы для света с длиной волны l равна D х. 6. Найти расстояние d между источниками монохроматического света S 1 и S 2 (длина волны l), если расстояния от щели до бипризмы и от бипризмы до экрана соответственно равны а и b, а ширина интерференционной полосы D х. 7. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной h. На сколько изменится оптическая длина пути, если волна падает на пластинку нормально? Показатель преломления стекла n.
Лабораторная работа № 42
С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Цель работы: Ознакомление с явлением интерференции на примере колец Ньютона и измерение длины световой волны. Приборы и принадлежности: Линза и плоскопараллельная пластина (в металлической оправе), измерительный микроскоп, объективный микрометр, светофильтры.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
При монохроматическом освещении в местах, где разность фаз Dj лучей, отраженных от верхней и нижней границ воздушной прослойки между линзой и пластинкой, равна 2p m (m = 1,2,..), возникают светлые кольца. Темные кольца возникают там, где Dj = (2 m + 1)p. (42.1) Разность фаз отраженных лучей определяется толщиной прослойки d с учетом изменения фазы световой волны на p при отражении от поверхности стеклянной пластинки Dj = 2p (2 d / l) + p. (42. 2) Согласно рис.42.1 d = R -
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 76; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.244 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||





 А
А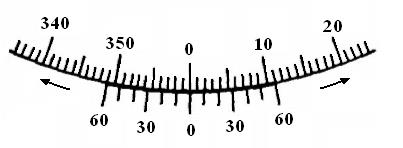
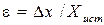 . (2)
. (2)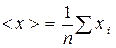 . (3)
. (3)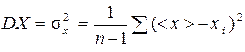 . (4)
. (4)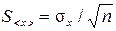 . (5)
. (5)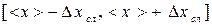 , в котором может оказаться истинное значение. Чем больше D хсл при прочих равных условиях, тем больше вероятность того, что истинное значение измеряемой величины Х находится в данном интервале.
, в котором может оказаться истинное значение. Чем больше D хсл при прочих равных условиях, тем больше вероятность того, что истинное значение измеряемой величины Х находится в данном интервале. 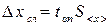 , (6)
, (6)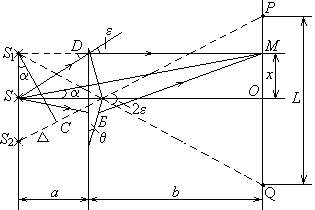 Рисунок 41.1
Рисунок 41.1
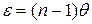 , (41.1)
где n – показатель преломления стекла бипризмы.
, (41.1)
где n – показатель преломления стекла бипризмы.
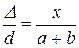 (41.2)
(41.2)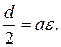 (41.3)
(41.3)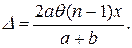 (41.4)
(41.4)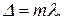
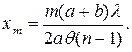 (41.5)
(41.5)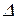 х, которую называют шириной интерференционной полосы. Из формулы (41.5) следует, что
х, которую называют шириной интерференционной полосы. Из формулы (41.5) следует, что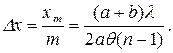 (41.6)
(41.6)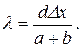 (41.7)
(41.7)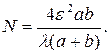 (41.8)
(41.8)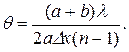 (41.9)
(41.9)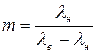 . (41.10)
. (41.10)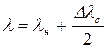 , соответствующую середине спектрального интервала, из (41.10) можно получить
, соответствующую середине спектрального интервала, из (41.10) можно получить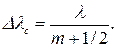 (41.11)
(41.11)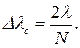 (41.12)
(41.12)
 d, (41.14)
d, (41.14)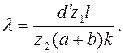 (41.15)
(41.15)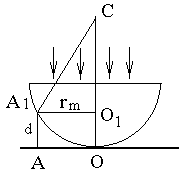
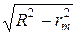 , где R – радиус кривизны сферической поверхности линзы, rm – радиус m - го кольца. П
, где R – радиус кривизны сферической поверхности линзы, rm – радиус m - го кольца. П 


