
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возведение оператора в степеньСодержание книги
Поиск на нашем сайте Оператор Алгебра операторов некоммутативна. Если в обычной алгебре a ۰ b = b ۰ a, то для операторов в общем случае Если коммутатор Коммутатор можно использовать, если необходимо переставить операторы. Например, из (5.4)
В квантовой механике используются только операторы линейные и самосопряженные (иначе – эрмитовые). Оператор ( Свойство самосопряженности, или эрмитовости, оператора интегральное. Оператор
Здесь функции
Здесь неизвестными являются как константа F, называемая собственным значением оператора Различных собственных значений F может быть много. Вся их совокупность образует спектр собственных значений. Спектр может быть дискретным – F = F 1, F 2, … Fn, … (n – квантовое число, нумерующее собственные значения). Если собственное значение F может принимать любые значения, то спектр называется непрерывным. Каждому собственному значению соответствует своя собственная функция. Так, если спектр дискретный, то уравнение (5.7) записывают в виде и каждому собственному значению Fn = F 1, F 2, … соответствует собственная функция φ n (ξ) (n = 1, 2, …). Если спектр непрерывный, то уравнение (5.7 ) записывают в виде или иначе – собственное значение F вносят в виде аргумента в собственную функцию, т.е. И здесь каждому собственному значению F соответствует своя собственная функция φ (F,ξ). Возможен случай, когда одному и тому же собственному значению F соответствует не одна, а несколько собственных функций: В этом случае говорят, что спектр вырожденный, а число fn – это кратность вырождения, т.е. число различных собственных функций φ nα (ξ), соответствующих собственному значению Fn. В случае вырождения собственная функция оператора несет два квантовых числа – n = 1, 2, … и α = 1, 2, …, fn. Лекция 6 МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ КВАНТОВОЙ МЕХАНИКИ Свойства собственных функций и собственных значений операторов
О собственных значениях Собственные значения эрмитовых операторов действительны. Покажем это. Возьмем уравнение (5.7) на собственные функции и собственные значения оператора
Умножим слева первое уравнение на φ *(ξ),а второе – на φ (ξ), вычтем из первого уравнения второе и результат проинтегрируем по всему пространству:
Здесь учтено, что для нормированных собственных функций (их также нормируют, как и волновую функцию)
В итоге F - F * = 0 и F = F *, что и требовалось доказать.
|
||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 называется n -ой степенью оператора
называется n -ой степенью оператора 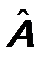 , если результаты действия на произвольную функцию Ψ оператора
, если результаты действия на произвольную функцию Ψ оператора 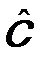 и n -кратного действия оператора
и n -кратного действия оператора  одинаковы:
одинаковы: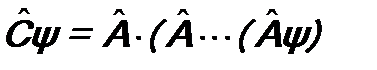 . (5.3)
. (5.3)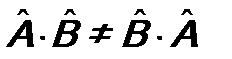 , т.е. они не коммутируют. Именно поэтому при перемножении операторов важно следить за их расстановкой в произведении. Для двух операторов
, т.е. они не коммутируют. Именно поэтому при перемножении операторов важно следить за их расстановкой в произведении. Для двух операторов 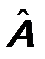 и
и  принято указывать коммутатор. Так называется оператор
принято указывать коммутатор. Так называется оператор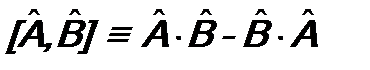 . (5.4)
. (5.4) равен нулю, т.е.
равен нулю, т.е. 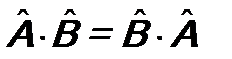 , говорят, что операторы коммутируют.
, говорят, что операторы коммутируют.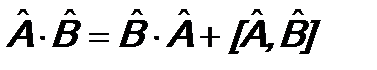 .
.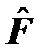 называется линейным, если он при действии на суперпозицию функций действует на каждое слагаемое в отдельности:
называется линейным, если он при действии на суперпозицию функций действует на каждое слагаемое в отдельности: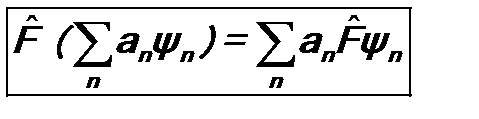 , (5.5)
, (5.5)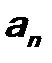 - произвольные коэффициенты).
- произвольные коэффициенты).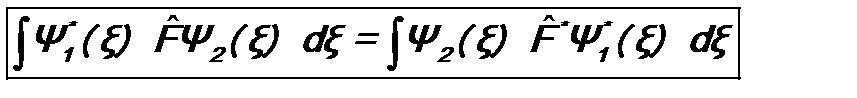 . (5.6)
. (5.6)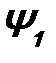 и
и  - произвольные, но должны удовлетворять стандартным условиям; интегрирование выполняется по всему пространству.
- произвольные, но должны удовлетворять стандартным условиям; интегрирование выполняется по всему пространству. В алгебре операторов одной из основных является задача нахождения собственных функций и собственных значений операторов. Для ее решения используется уравнение:
В алгебре операторов одной из основных является задача нахождения собственных функций и собственных значений операторов. Для ее решения используется уравнение: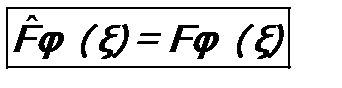 . (5.7)
. (5.7)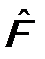 , так и функция
, так и функция 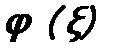 - собственная функция оператора
- собственная функция оператора  , n = 1, 2, …, (5.8)
, n = 1, 2, …, (5.8)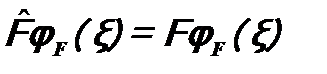 , (5.9)
, (5.9)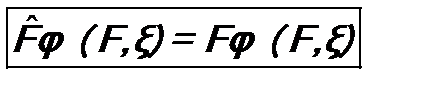 . (5.9*)
. (5.9*)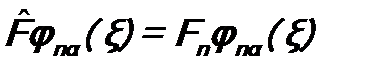 , α = 1, 2, …, fn. (5.10)
, α = 1, 2, …, fn. (5.10)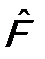 и комплексно сопряженное ему:
и комплексно сопряженное ему: ;
;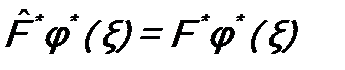 .
.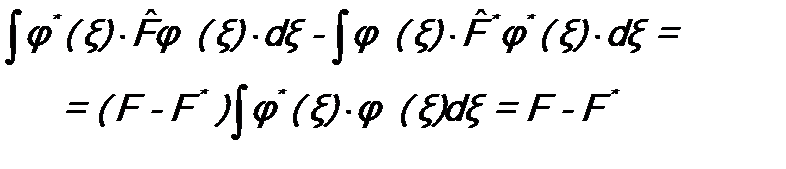 .
.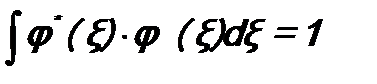 (см. (4.4)). Для эрмитовых, или самосопряженных, операторов имеет место соотношение (5.6). Учитывая произвольность в нем функций Ψ1 (ξ) и Ψ2 (ξ), полагая в нем Ψ1 (ξ)= Ψ2 (ξ)= φ (ξ), получим:
(см. (4.4)). Для эрмитовых, или самосопряженных, операторов имеет место соотношение (5.6). Учитывая произвольность в нем функций Ψ1 (ξ) и Ψ2 (ξ), полагая в нем Ψ1 (ξ)= Ψ2 (ξ)= φ (ξ), получим: .
.


