
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Все они впоследствии стали лауреатами нобелевской премии по физике.Стр 1 из 13Следующая ⇒
Основоположниками квантовой механики считаются Нильс Бор, Макс Планк, Альберт Эйнштейн, Луи де Бройль, Эрвин Шредингер, Вернер Гейзенберг. Все они впоследствии стали лауреатами Нобелевской премии по физике.
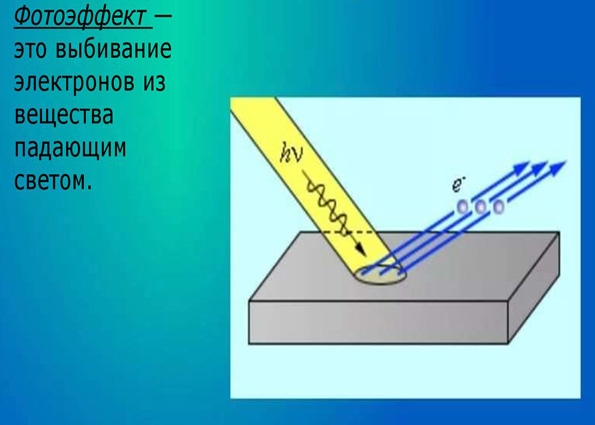
Лекция 1 ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ: ЯВЛЕНИЯ, ОБУСЛОВЛЕННЫЕ ВЗАИМОДЕЙСТВИЕМ СВЕТА С ВЕЩЕСТВОМ Основные явления, которые в этой области не могла объяснить классическая физика, это: Законы теплового излучения (и поглощения) абсолютно черного тела; 2) фотоэффект. Абсолютно черное тело – тело, поглощающее полностью попадающее на него электромагнитное излучение, в частности, тепловое или оптическое.
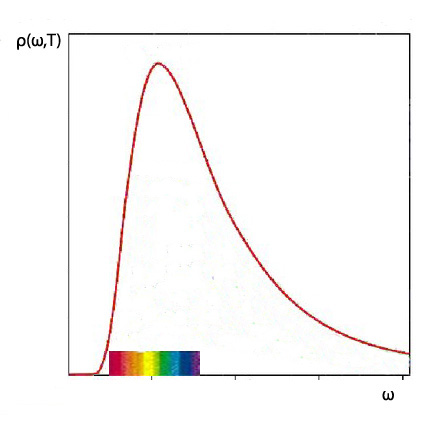
Модель абсолютно черного тела Введем плотность излучения где На эксперименте вначале отверстие закрывают, нагревают черное тело до температуры Т, и из-за колебаний частиц в стенках полости она заполняется равновесным тепловым излучением. Затем отверстие открывают и исследуют спектр выходящего теплового излучения. Законы: а). Вид спектра излучения (и поглощения) (впоследствии его назвали «планковским»).
Особенности спектра: 1. Распределение энергии по спектру неоднородное и зависит от температуры. При этом функция ρ(ω, Т) →0 при ω →0 и ω → ∞. Площадь под кривой существенно зависит от температуры. 3. Частота, определяющая положение максимума, ω m б). Закон Вина При больших частотах ρ(ω,Т) (константа b >0). в). Закон Стефана-Больцмана Полная энергия излучения (площадь под кривой)
(σ – постоянная Стефана-Больцмана). Классическая теория для плотности излучения дает закон Релея-Джинса: ρ(ω,Т) Видно, что ρ(ω,Т) → Этот результат известен под названием: «ультрафиолетовая катастрофа». Фотоэффект
С позиций классической физики нельзя было объяснить второй закон фотоэффекта. Почему? Электрон обладает электрическим зарядом – e. При облучении вещества со стороны электромагнанитной волны на него будет действовать сила
В результате кинетическая энергия вылетевшего электрона Чтобы устранить противоречия между экспериментом и классической физикой, необходимы были новые идеи. Они были сформулированы М.Планком и А.Эйнштейном. Оба ученых сделали предположение: Из этого «закона Планка» получаются и закон Релея-Джинса, и закон Вина. При малых частотах, когда можно считать Подставив (1.2) в (1.1), получим: При больших частотах, когда можно считать единицей в знаменателе (1.1) можно пренебречь. Тогда Объяснение законам фотоэффекта дал А. Эйнштейн. Он предположил, что само световое излучение состоит из квантов – из фотонов. Фотон – это частица, обладающая энергией При облучении светом вещества электрон поглощает фотон. Энергия фотона тратится на преодоление энергетического барьера для электрона на границе вещества (это работа выхода W вых.) и его кинетическую энергию ԑ. Иными словами, из закона сохранения энергии следует: Из (1.3) видно, что энергия вылетающего электрона зависит только от частоты излучения (работа выхода W вых. для конкретного вещества является константой), как и следует из эксперимента.
Итак, и в теории излучения черного тела М. Планка, и в теории фотоэффекта А. Эйнштейна преодоление трудностей классической физики было найдено в реализации идеи дуализма (двойственной природы) света. Как оказалось, свет может проявлять и свойства волн (это его волновая природа, известная в классической макрофизике), и свойства частиц – фотонов (новое представление при трактовке явлений на уровне микромира). Именно последнее обстоятельство обеспечило успех теории и заложило фундамент квантовой механики.
Лекция 2 ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ: ЯВЛЕНИЯ, ОБУСЛОВЛЕННЫЕ АТОМНОЙ И МОЛЕКУЛЯРНОЙ СТРУКТУРОЙ ВЕЩЕСТВА
Основные явления, которые в этой области не могла объяснить классическая физика: Экспериментально было показано, что некоторые физические характеристики атомов являются дискретными. Так, в опытах Франка-Герца была доказана дискретность величины энергии, которую могут принимать атомы ртути при столкновениях с электронами. В экспериментах Штерна-Герлаха была продемонстрирована дискретность проекции момента количества движения атома на заданное направление, т.е. пространственное квантование у атомов.
Недостатки теории. Даже его спектр. Что такой путь правильный. Однако требовались новые идеи. Лекция 3 ГИПОТЕЗА ДЕ БРОЙЛЯ И ЕЕ ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ
Объяснение явлений, обусловленных взаимодействием с веществом электромагнитного излучения, было получено в предположении, что последнее имеет двойственную природу – проявляет и свойства волн, и свойства частиц в виде фотонов. Это дуализм «волна-частица». Тем не менее, гипотеза де Бройля требовала экспериментального подтверждения. Надо было показать, что микрочастицы, обладая свойствами волн, могут дифрагировать и интерферировать. Эти явления являются особенностью только волнового движения.
Является общепринятой Частица в потенциальной яме с бесконечно высокими стенками Физический смысл волновой функции остается таким же, как и у волны де Бройля: квадрат модуля волновой функции в момент времени t.
Возьмем элемент объема dV (иначеего обозначают как d 3 r, в декартовой системе координат (x, y, z) → dV = dx ۰ dy ۰ dz, в сферической системе координат (r, θ, φ) → dV = r 2 ۰ dr ۰ dΩ, где dΩ = sinθ ۰ dθ ۰ dφ – элемент телесного угла). Тогда дифференциальная вероятность dw обнаружить микрочастицу в этом элементе объема будет (по М. Борну): Величина По теореме сложения вероятностей вероятность обнаружить микрочастицу вообще где-то в пространстве Это условие нормировки волновой функции. Оно используется для определения произвольной константы, которая обычно возникает при нахождении волновой функции. Эта константу называют нормировочной. От волновой функции требуется выполнение стандартных условий. Это: а) конечность; б) непрерывность; в) однозначность. Суммируем сказанное.
Если микрочастица не одна и их количество N, то волновая функция будет зависеть от координат всех микрочастиц: всех частиц, каждую в своей пространственной точке Условие нормировки будет иметь вид: Часто весь набор координат
Лекция 5 МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ КВАНТОВОЙ МЕХАНИКИ. ОПЕРАТОРНЫЙ ФОРМАЛИЗМ
Микрочастицы обладают как свойствами частиц, так и волн – это «корпускулярно-волновой дуализм». Как следствие, математический аппарат классической физики для них не применим. Для описания состояния микрочастиц используется операторный формализм.
Пусть имеются две функции одного класса: Иными словами, оператор – это символ, который показывает, какое действие следует произвести над функцией данного класса, чтобы получить другую функцию того же класса. Арифметика операторов. Сложение операторов Оператор Естественно, что вместо знака (+) Умножение операторов Оператор Каждой динамической переменной классической механики в квантовой механике сопоставляется линейный эрмитовый оператор. Соотношение между операторами такое же, как и между динамическими переменными в классической механике. В классической механике для характеристики состояния системы используются динамические переменные:
Квантовая механика использует операторный формализм. Физические операторы имеют вид (вид некоторых из них впоследствии будет обоснован из свойств пространства-времени и законов сохранения): а). Оператор координаты Его действие на функцию сводится просто к умножению этой функции на соответствующую координату, т.е.
аналогично действие операторной функции
б). Оператор импульса
Соответственно векторный оператор импульса
Таким образом, в). Оператор момента импульса В классической механике оператор момента импульса имеет вид:
= = Отсюда следует, что компоненты векторного оператора
Наряду с операторами Операторы оператор Поскольку физически момент импульса связан с поворотами системы в пространстве, часто удобнее пользоваться его определением в сферической системе координат (r, θ, φ). В этой системе наиболее используемые на практике операторы
г). Оператор энергии Приведем сначала вид оператора кинетической энергии
Здесь m и
Δ – оператор Лапласа. Здесь использован вид операторов В классической механике полная энергия частицы равна:
Здесь
или Нередко требуется оператор Гамильтона не в декартовой, а в сферической системе координат. Он имеет вид:
Таблица физических операторов
Дискретный спектр Предположим, что нас интересует физическая величина F с дискретным спектром и для ее оператора
Здесь коэффициенты разложения an имеют вид (см. формулу (6.4)): Подставим Ψ(ξ) в виде (8.3) и аналогичное разложение для Ψ*(ξ) в выражение(8.1)для среднего значения
Кроме того, коэффициенты разложения an в (8.3) удовлетворяют критерию полноты (см. (6.5)): Предположим, что нам была бы известна вероятность Wn (F = Fn) того, что при измерении величины F будет получено конкретное значение F = Fn. Тогда величину при условии, что Из сравнения формул (8.7) и (8.5), а также (8.6) и (8.8), следует: Это и есть искомая вероятность результата измерения физической величины. Для ее расчета следует разложить волновую функцию Ψ(ξ) в ряд по собственным функциям φ1(ξ), φ2(ξ), …, φ n (ξ), … оператора Непрерывный спектр В случае, если оператор
и сравнить результаты. При этом еще надо учесть, что коэффициент разложения a (F) имеет вид (см. ф-лу (6.11))
и для него выполняется критерий полноты (ф-ла (6.12)):
В итоге получается, что искомую плотность вероятностиW (F) можно вычислить по формуле, аналогичной ф-ле (8.9): Соответственно дифференциальная вероятность имеет вид:
Лекция 9 ВРЕМЕННОЕ УРАВНЕНИЕ ШРЁДИНГЕРА.
Уравнение Шрёдингера позволяет находить вид волновой функции микрочастицы или системы микрочастиц. В соответствии с постулатом 1 волновая функция Ψ(ξ, t) определяет все свойства системы в данный момент времени t. Это означает, что волновая функция Ψ(ξ, t) определяет и то, как система будет меняться в будущем. Иными словами, функция Ψ(ξ, t) должна определять, как будет изменяться в будущем и ее первая производная по времени. Поэтому можно написать
где
где оператор В общем случае Для нахождения координатной зависимости оператора
В итоге При подстановке (см. ф-лу (7.8)). Поэтому в уравнении (9.1) можно считать, что
В итоге Из сравнения (9.2) и (9.3) следует, что уравнение (9.1) удовлетворяется тождественно при одновременной замене
Пусть на микрочастицу действует силовое поле, описываемое потенциальной функцией
Уравнение (9.6) с оператором Особенностью уравнения Шрёдингера является наличие в нем мнимой единицы i. Это дифференциальное уравнение есть первого порядка по времени. Обычно в физике уравнения такого рода описывают необратимые процессы, например, процессы диффузии или теплопроводности. Из-за мнимой единицы уравнение Шрёдингера допускает и периодические решения. Из-за наличия в уравнении потенциальной функции Наконец, дифференциальное уравнение первого порядка по времени требует задания начального условия, т.е. вида в начальный момент времени волновой функции Можно записать уравнение Шрёдингера и для системы из N микрочастиц:
Здесь mj - масса j -ой частицы,
СОХРАНЕНИЕ ЧИСЛА ЧАСТИЦ В КВАНТОВОЙ МЕХАНИКЕ
В классической механике закон сохранения числа частиц следует из уравнения непрерывности
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.81.94 (0.177 с.) |

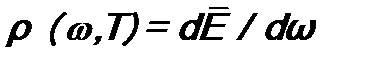 ,
, - энергия излучения, приходящаяся на интервал частот
- энергия излучения, приходящаяся на интервал частот 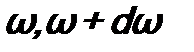 .
.
 Т.
Т.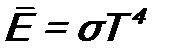
 T.
T. , когда ω →
, когда ω →  =
= 

 , где
, где  - напряженность электрического поля. Следовательно, ускорение электрона
- напряженность электрического поля. Следовательно, ускорение электрона 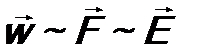 и скорость вылетающего электрона тоже пропорциональна
и скорость вылетающего электрона тоже пропорциональна  :
: 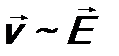 .
.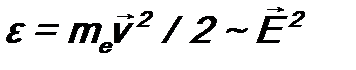 . В электродинамике величина
. В электродинамике величина 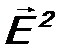 определяет интенсивность электромагнитной волны, т.е. энергия электрона должна зависеть от интенсивности, а не от длины волны (или частоты).
определяет интенсивность электромагнитной волны, т.е. энергия электрона должна зависеть от интенсивности, а не от длины волны (или частоты).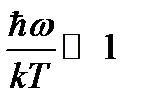 , экспоненту можно разложить в ряд, оставив только два члена разложения:
, экспоненту можно разложить в ряд, оставив только два члена разложения: . (1.2)
. (1.2)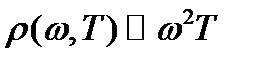 , что соответствует закону Релея-Джинса.
, что соответствует закону Релея-Джинса. ,
,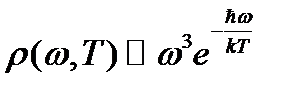 , что соответствует закону Вина, причем константа
, что соответствует закону Вина, причем константа  .
.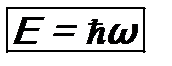 и импульсом
и импульсом 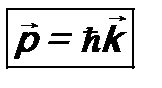 , где
, где  - волновой вектор, направленный в сторону распространения излучения (
- волновой вектор, направленный в сторону распространения излучения (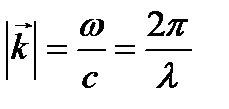 ).
). . (1.3)
. (1.3)



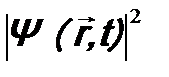 определяет вероятность обнаружения микрочастицы в данном месте пространства
определяет вероятность обнаружения микрочастицы в данном месте пространства 
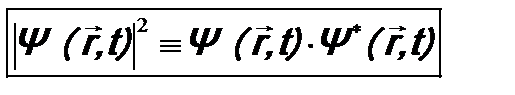 . (4.1)
. (4.1)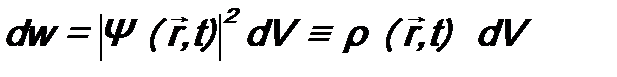 . (4.2)
. (4.2)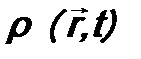 называется плотностью вероятности:
называется плотностью вероятности: . (4.3)
. (4.3)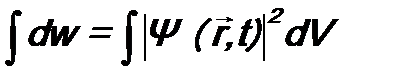 будет достоверным событием. Следовательно,
будет достоверным событием. Следовательно,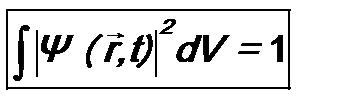 . (4.4)
. (4.4)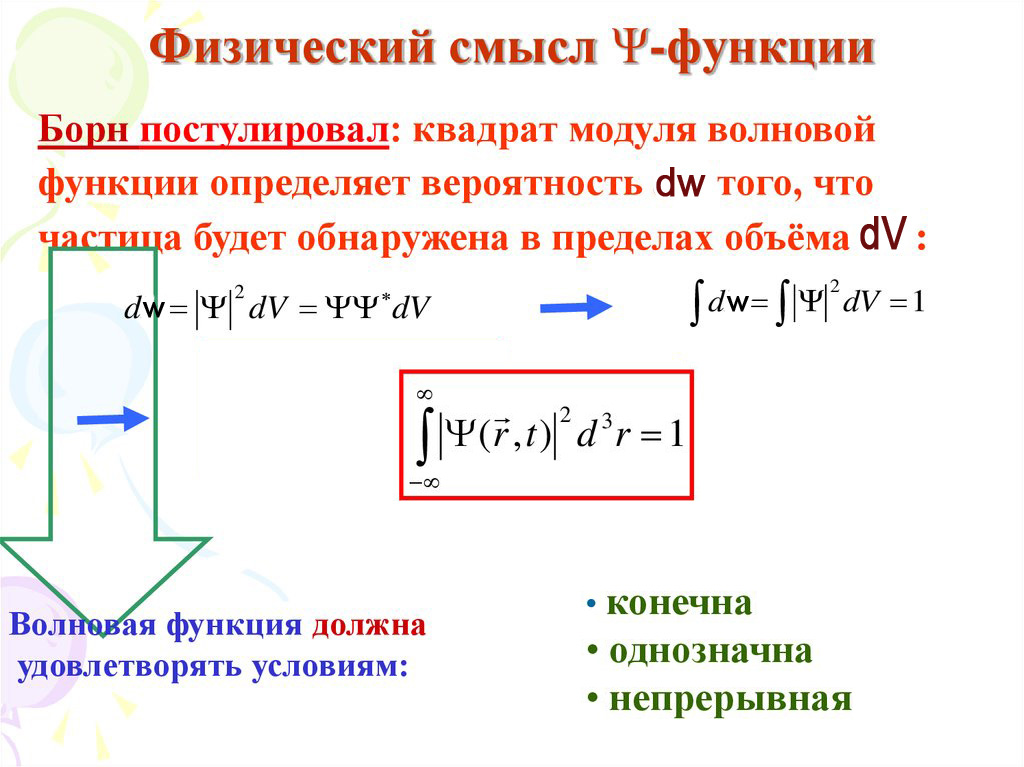
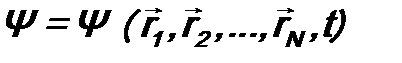 . Тогда величина
. Тогда величина  дает в момент времени tвероятностьодновременного обнаружения
дает в момент времени tвероятностьодновременного обнаружения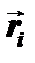 (i = 1, 2,…, N).
(i = 1, 2,…, N). .
.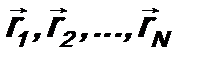 обозначают одной буквой ξ, т.е. ξ = (
обозначают одной буквой ξ, т.е. ξ = (  .
. и
и  . Если есть математическая операция (обозначим ее
. Если есть математическая операция (обозначим ее  ), которая переводит функцию
), которая переводит функцию  , то
, то 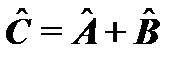 называется суммой операторов
называется суммой операторов 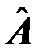 и
и 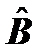 , если результаты действия на произвольную функцию Ψ операторов
, если результаты действия на произвольную функцию Ψ операторов  и
и 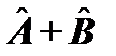 будут одинаковы:
будут одинаковы: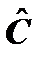 Ψ =
Ψ = 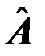 Ψ
Ψ  Ψ. (5.1)
Ψ. (5.1)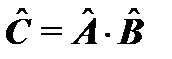 называется произведением операторов
называется произведением операторов  будут одинаковы:
будут одинаковы: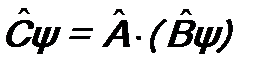 . (5.2)
. (5.2)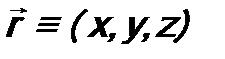 - координата,
- координата,  - импульс,
- импульс, 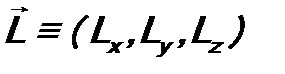 - момент импульса (иначе – момент количества движения), E - энергия.
- момент импульса (иначе – момент количества движения), E - энергия. .
.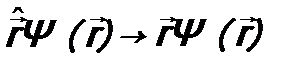 ;
; от
от  сводится просто к умножению на функцию
сводится просто к умножению на функцию 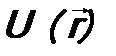 , т.е.
, т.е. .
.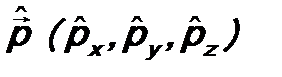 .
.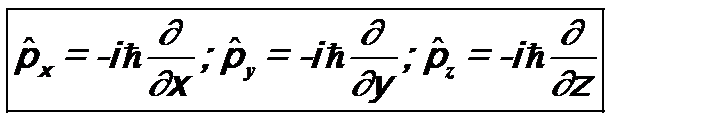 . (7.1)
. (7.1)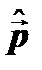 имеет вид:
имеет вид: . (7.2)
. (7.2) выражается через известный в векторной алгебре оператор «набла»:
выражается через известный в векторной алгебре оператор «набла»: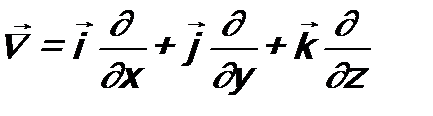 . (7.3)
. (7.3) .
. (
(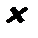 - знак векторного произведения). В соответствии с постулатом 3 оператор момента импульса будет иметь вид:
- знак векторного произведения). В соответствии с постулатом 3 оператор момента импульса будет иметь вид: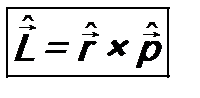 . (7.4)
. (7.4)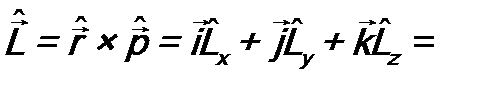
 =
=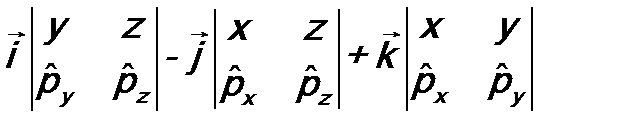 =
=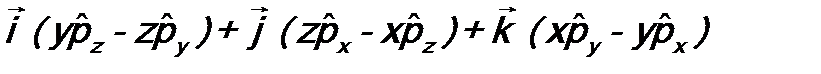 .
. 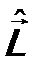 имеют вид:
имеют вид: . (7.5)
. (7.5) обычно рассматривают и оператор квадрата момента импульса
обычно рассматривают и оператор квадрата момента импульса  :
: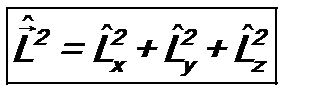 (7.6)
(7.6)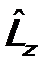 и
и 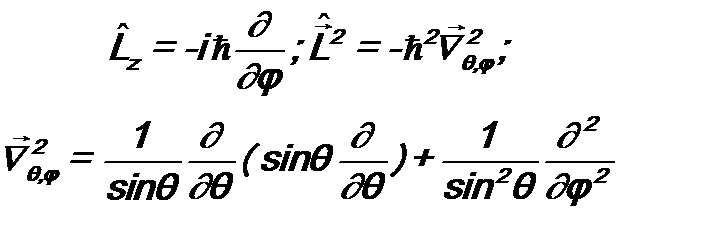 . (7.7)
. (7.7)  . В классической механике выражение для кинетической энергии имеет вид:
. В классической механике выражение для кинетической энергии имеет вид: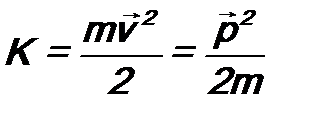 .
. - масса и скорость частицы,
- масса и скорость частицы, 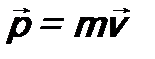 - ее импульс. В квантовой механике вводится лишь оператор импульса. Тогда в соответствии с постулатом 3 оператор кинетической энергии будет иметь вид:
- ее импульс. В квантовой механике вводится лишь оператор импульса. Тогда в соответствии с постулатом 3 оператор кинетической энергии будет иметь вид: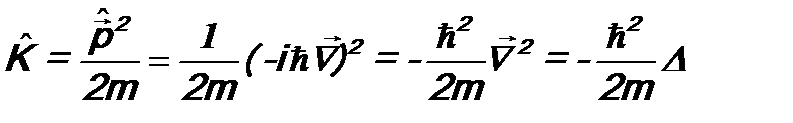 . (7.8)
. (7.8) (см. ф-лы (7.2) и (7.3)) и учтено, что
(см. ф-лы (7.2) и (7.3)) и учтено, что . (7.9)
. (7.9) .
. - потенциальная энергия частицы,
- потенциальная энергия частицы,  - функция Гамильтона. В соответствии постулатом 3 оператор полной энергии микрочастицы будет иметь вид:
- функция Гамильтона. В соответствии постулатом 3 оператор полной энергии микрочастицы будет иметь вид: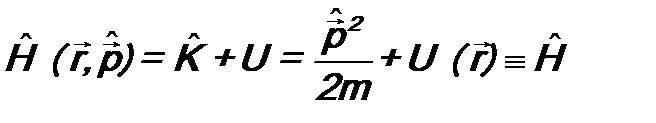 . (7.10)
. (7.10)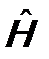 называется оператором Гамильтона. В явном виде
называется оператором Гамильтона. В явном виде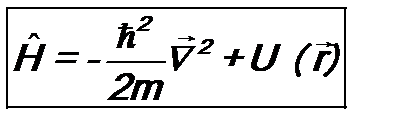 , (7.11)
, (7.11)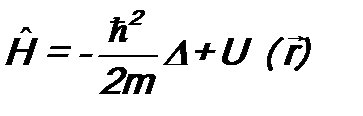 . (7.12)
. (7.12)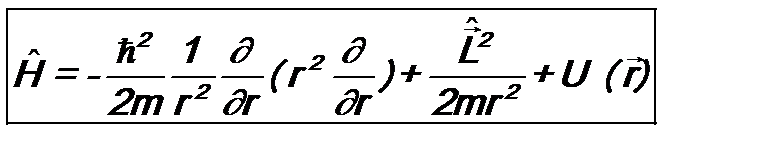 . (7.13)
. (7.13)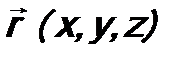 и
и  ;
;  ;
; 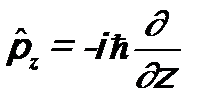 .
.
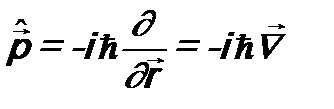 ;
;  ,
, 

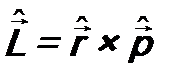
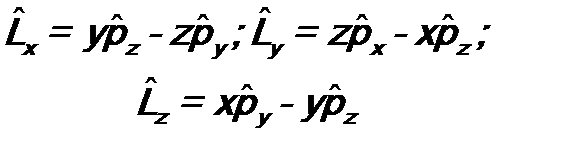
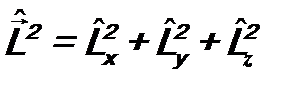
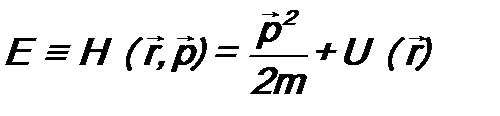

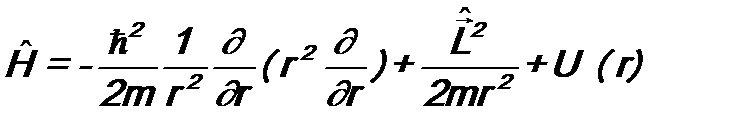
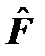 известны собственные функции и собственные значения, т.е. известно решение уравнения
известны собственные функции и собственные значения, т.е. известно решение уравнения . (8.3)
. (8.3)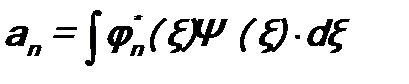 . (8.4)
. (8.4)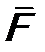 :
: .
.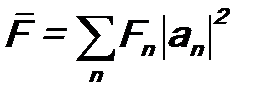 . (8.5)
. (8.5) . (8.6)
. (8.6)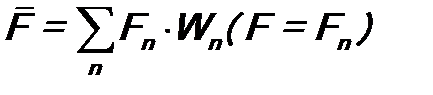 (8.7)
(8.7)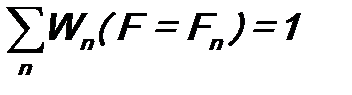 . (8.8)
. (8.8)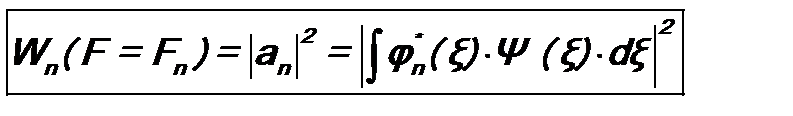 . (8.9)
. (8.9)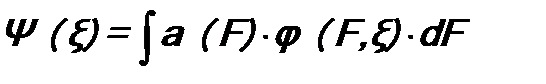

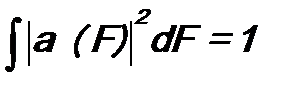 .
.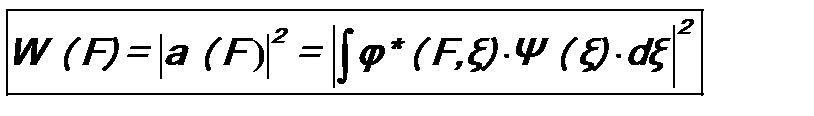 . (8.10)
. (8.10) .
. 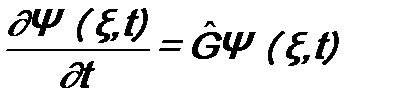 ,
,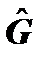 - пока неизвестный нам оператор с размерностью [время]-1, решающий поставленную задачу. Для дальнейшего удобно его переопределить:
- пока неизвестный нам оператор с размерностью [время]-1, решающий поставленную задачу. Для дальнейшего удобно его переопределить: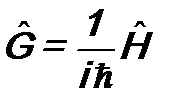 ,
, также пока не известен. Так как размерность постоянной Планка
также пока не известен. Так как размерность постоянной Планка 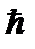 - это [энергия·время], то оператор
- это [энергия·время], то оператор  . (9.1)
. (9.1)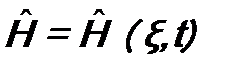 . Про зависимость от пространственной переменной пока ничего не известно, а вот от времени t оператор
. Про зависимость от пространственной переменной пока ничего не известно, а вот от времени t оператор 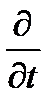 . Но цель уравнения (9.1) как раз и выразить первую производную от волновой функции через саму эту функцию, и с помощью оператора
. Но цель уравнения (9.1) как раз и выразить первую производную от волновой функции через саму эту функцию, и с помощью оператора  не только через Ψ(ξ, t), как требуется, но еще и через нее саму же. Иными словами, оператор
не только через Ψ(ξ, t), как требуется, но еще и через нее саму же. Иными словами, оператор  . Тогда для полного определения состояния системы в момент времени t =0 требуется задать в этот момент времени не только саму волновую функцию Ψ(ξ, t =0), но и ее первую производную
. Тогда для полного определения состояния системы в момент времени t =0 требуется задать в этот момент времени не только саму волновую функцию Ψ(ξ, t =0), но и ее первую производную 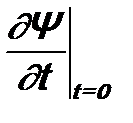 . Это противоречит постулату 1, согласно которому все должна определять только волновая функция Ψ(ξ, t =0). Помимо этой функции, для полного определения состояния системы в момент времени t =0 дополнительно потребуются и другие функции, если в операторе
. Это противоречит постулату 1, согласно которому все должна определять только волновая функция Ψ(ξ, t =0). Помимо этой функции, для полного определения состояния системы в момент времени t =0 дополнительно потребуются и другие функции, если в операторе 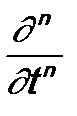 , n =3, 4, … Это опять будет противоречить постулату 1. Аналогичная ситуация будет возникать и тогда, когда в операторе
, n =3, 4, … Это опять будет противоречить постулату 1. Аналогичная ситуация будет возникать и тогда, когда в операторе 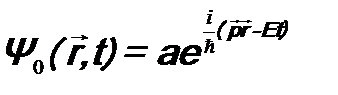 . Будем рассматривать нерелятивистскую задачу, поэтому можно считать:
. Будем рассматривать нерелятивистскую задачу, поэтому можно считать:  . Подставим
. Подставим 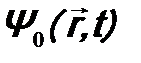 в уравнение (9.1) и подберем так вид оператора
в уравнение (9.1) и подберем так вид оператора  .
. . (9.2)
. (9.2)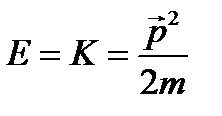 . В соответствии с постулатом 3 оператор кинетической энергии
. В соответствии с постулатом 3 оператор кинетической энергии 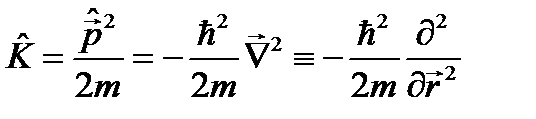
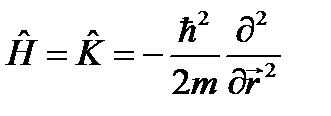 . Подставим этот оператор и функцию
. Подставим этот оператор и функцию 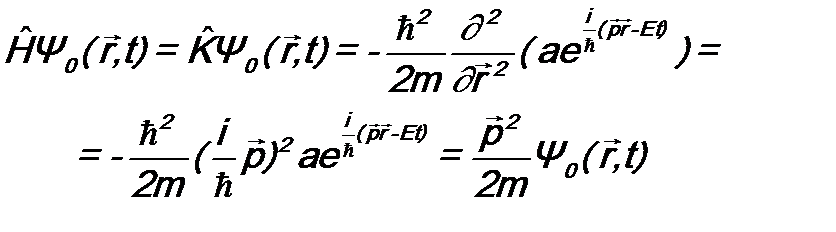 .
.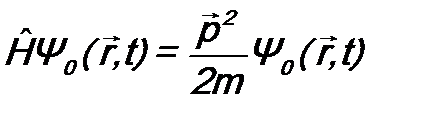 . (9.3)
. (9.3)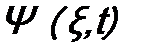 →
→ 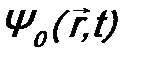 и оператора
и оператора 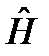 на оператор кинетической энергии
на оператор кинетической энергии 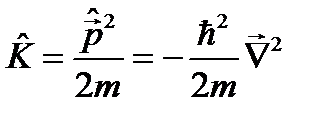 . Иными словами, для свободно движущейся частицы уравнение (9.1) имеет вид:
. Иными словами, для свободно движущейся частицы уравнение (9.1) имеет вид: ; (9.4)
; (9.4) . (9.5)
. (9.5) . Постулируется, что оператор
. Постулируется, что оператор 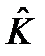 , следует заменить на оператор
, следует заменить на оператор 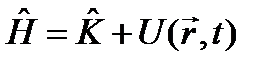 . В итоге для нахождения волновой функции микрочастицы
. В итоге для нахождения волновой функции микрочастицы 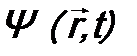 получится уравнение:
получится уравнение: ; (9.6)
; (9.6)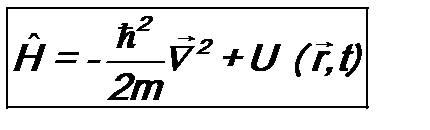 . (9.7)
. (9.7) Э. Шрёдингером и называется: «Уравнение Шрёдингера». Это основное уравнение квантовой механики. Оно позволяет найти волновую функцию микрочастицы, содержащую всю необходимую физическую информацию о ее состоянии. Оператор
Э. Шрёдингером и называется: «Уравнение Шрёдингера». Это основное уравнение квантовой механики. Оно позволяет найти волновую функцию микрочастицы, содержащую всю необходимую физическую информацию о ее состоянии. Оператор 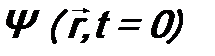 . Для ее нахождения поступают следующим образом. В начальный момент времени t =0 из эксперимента для микрочастицы определяют набор физических величин L, M, N, …, которые одновременно имеют определенные значения. Их число должно быть равно числу степеней свободы у микрочастицы. Можно показать, что соответствующие физические операторы
. Для ее нахождения поступают следующим образом. В начальный момент времени t =0 из эксперимента для микрочастицы определяют набор физических величин L, M, N, …, которые одновременно имеют определенные значения. Их число должно быть равно числу степеней свободы у микрочастицы. Можно показать, что соответствующие физические операторы 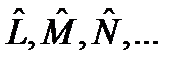 будут коммутировать друг с другом. Как упоминалось в конце лекции 6, операторы такого рода будут иметь общую систему собственных функций. Произведение этих функций и будет определять
будут коммутировать друг с другом. Как упоминалось в конце лекции 6, операторы такого рода будут иметь общую систему собственных функций. Произведение этих функций и будет определять 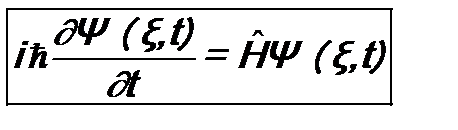 ,
,  ; (9.8)
; (9.8)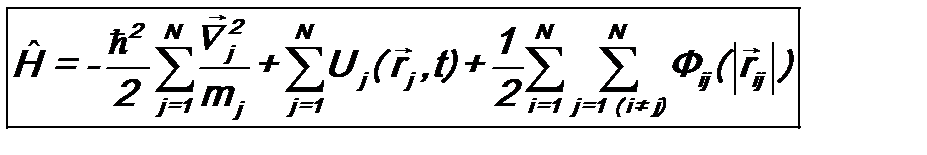 . (9.9)
. (9.9)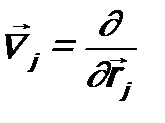 ,
, 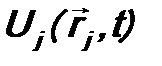 - потенциальная функция, характеризующая силовое поле, которое действует на j -ую частицу,
- потенциальная функция, характеризующая силовое поле, которое действует на j -ую частицу, 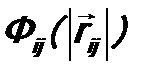 - потенциальная энергия взаимодействия i -ой и j -ой частиц,
- потенциальная энергия взаимодействия i -ой и j -ой частиц, 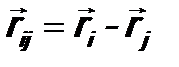 - расстояние между ними.
- расстояние между ними. Лекция 10
Лекция 10


