
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектр собственных значений физического оператора тождественен наблюдаемому спектру соответствующей физической величины.
При решении уравнения на собственные функции и собственные значения физического оператора
Рассмотрим некоторые следствия этого постулата. а). Предположим, что состояние микрочастицы описывается волновой функцией Ψ(ξ) (время не имеет значения и мы его не включаем). Пусть для физического оператора F = F n. В этом случае говорят, что физическая величина F имеетопределенное значение. Например, спектр собственных значений и собственные функции оператора (m = 0, ±1, ±2 …). Если волновая функция будет совпадать с одной из собственных б). Предположим, что волновая функция не совпадает ни с одной из собственных функций: Ψ(ξ) (n =1, 2, …). Тогда не имеетопределенного значения. Так, если в приведенном выше примере Ψ (m = 0, ±1, ±2 …), то при измерении величины Lz будут получаться разнообразные значения, но они будут обязательно из спектра собственных значений оператора В отличие от квантовой механики в классической механике термина «физическая величина не имеет определенного значения» не существует!
Лекция 8 СРЕДНЕЕ ЗНАЧЕНИЕ И ВЕРОЯТНОСТЬ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ
О среднем значении Пусть задано состояние микрочастицы, т.е. известна ее волновая функция Ψ(ξ) (в ее аргументы, как и выше, временную переменную пока не включаем). Также допустим, что в этом состоянии интересующая нас физическая величина F не имеет определенного значения. Тогда при ее измерении будут получаться различные значения F 1, F 2, …, F n, … из спектра собственных значений оператора величины F. Его можно рассчитать по формуле: где предполагается, что волновая функция нормирована:
Если этого нет, то вычисление Можно доказать следующие свойства среднего значения: а). Для эрмитовых операторов б). Если волновая функция Ψ(ξ) совпадает с собственной функцией оператора Ψ(ξ)=φ n (ξ), то
О вероятности результата измерения физической величины
Дискретный спектр Предположим, что нас интересует физическая величина F с дискретным спектром и для ее оператора
Здесь коэффициенты разложения an имеют вид (см. формулу (6.4)): Подставим Ψ(ξ) в виде (8.3) и аналогичное разложение для Ψ*(ξ) в выражение(8.1)для среднего значения
Кроме того, коэффициенты разложения an в (8.3) удовлетворяют критерию полноты (см. (6.5)): Предположим, что нам была бы известна вероятность Wn (F = Fn) того, что при измерении величины F будет получено конкретное значение F = Fn. Тогда величину при условии, что Из сравнения формул (8.7) и (8.5), а также (8.6) и (8.8), следует: Это и есть искомая вероятность результата измерения физической величины. Для ее расчета следует разложить волновую функцию Ψ(ξ) в ряд по собственным функциям φ1(ξ), φ2(ξ), …, φ n (ξ), … оператора Непрерывный спектр В случае, если оператор
и сравнить результаты. При этом еще надо учесть, что коэффициент разложения a (F) имеет вид (см. ф-лу (6.11))
и для него выполняется критерий полноты (ф-ла (6.12)):
В итоге получается, что искомую плотность вероятностиW (F) можно вычислить по формуле, аналогичной ф-ле (8.9): Соответственно дифференциальная вероятность имеет вид:
Лекция 9 ВРЕМЕННОЕ УРАВНЕНИЕ ШРЁДИНГЕРА.
Уравнение Шрёдингера позволяет находить вид волновой функции микрочастицы или системы микрочастиц. В соответствии с постулатом 1 волновая функция Ψ(ξ, t) определяет все свойства системы в данный момент времени t. Это означает, что волновая функция Ψ(ξ, t) определяет и то, как система будет меняться в будущем. Иными словами, функция Ψ(ξ, t) должна определять, как будет изменяться в будущем и ее первая производная по времени. Поэтому можно написать
где
где оператор В общем случае
Для нахождения координатной зависимости оператора
В итоге При подстановке (см. ф-лу (7.8)). Поэтому в уравнении (9.1) можно считать, что
В итоге Из сравнения (9.2) и (9.3) следует, что уравнение (9.1) удовлетворяется тождественно при одновременной замене
Пусть на микрочастицу действует силовое поле, описываемое потенциальной функцией
Уравнение (9.6) с оператором Особенностью уравнения Шрёдингера является наличие в нем мнимой единицы i. Это дифференциальное уравнение есть первого порядка по времени. Обычно в физике уравнения такого рода описывают необратимые процессы, например, процессы диффузии или теплопроводности. Из-за мнимой единицы уравнение Шрёдингера допускает и периодические решения. Из-за наличия в уравнении потенциальной функции Наконец, дифференциальное уравнение первого порядка по времени требует задания начального условия, т.е. вида в начальный момент времени волновой функции Можно записать уравнение Шрёдингера и для системы из N микрочастиц:
Здесь mj - масса j -ой частицы,
СОХРАНЕНИЕ ЧИСЛА ЧАСТИЦ В КВАНТОВОЙ МЕХАНИКЕ
В классической механике закон сохранения числа частиц следует из уравнения непрерывности Здесь
Умножим первое уравнение на
Проинтегрируем обе части этого выражения по ξ.
Здесь учтена эрмитовость гамильтониана, в соответствии с которой (см. (5.6)). Итак, получили: Это соотношение можно рассматривать как законсохранения числа частиц в интегральном виде. Действительно, из вероятностной трактовки волновой функции следует, что величина Из (10.3) вытекает еще одно следствие. Интеграл не изменяется, т.е. const (t) будет константой и по времени t. Из соотношения (10.2) можно получить закон сохранения микрочастиц в дифференциальном виде. Подставим в (10.2) оператор
Плотность вероятности
и назовем ее плотностью тока вероятности. Тогда соотношение (10.4) можно представить в виде: Здесь учтено, что
Из сравнения уравнений (10.1) и (10.6) следует, что их вид одинаков, только в последнем случае обозначения Например, умножив уравнение (10.6) на электрический заряд микрочастицы e, получим закон сохранения заряда в дифференциальном виде:
Здесь Обратим внимание, что, как это следует из определения (10.5), плотность тока вероятности
Лекция 11 УРАВНЕНИЕ ШРЁДИНГЕРА ДЛЯ СТАЦИОНАРНЫХ СОСТОЯНИЙ
Для нахождения волновой функции временным уравнением Шрёдингера имеет смысл пользоваться только тогда, когда явно зависит от времени гамильтониан Пусть гамильтониан не зависит от времени: Ищем волновую функцию в виде:
Величина E – константа с размерностью энергии. Введена она потому, что в (11.3) левая сторона зависит только от t, а правая сторона – только от ξ. Поэтому равенство возможно, только если и правая, и левая стороны будут константами. Из (11.3) получаются два уравнения: Интегрирование в (11.4) дает: Константа интегрирования положена равной 1, так как общая константа в (11.2) все равно будет находиться из условия нормировки. Уравнение (11.5) позволяет найти волновую функцию Состояние с определенным значением энергии E называется стационарным, а уравнение (11.5) называется уравнением Шрёдингера для стационарных состояний. Итак, в случае одной микрочастицы ( а величины функции (11.9) принимают вид Во втором случае –
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.87 (0.092 с.) |
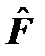 находятспектр собственных значений. Например, в случае дискретного спектра – это { F 1, F 2, …, F n, … }. С другой стороны, на эксперименте измеряют физическую величину F и тоже получают ее спектр. Постулат 4 устанавливает связь этой математики квантовой механики с физикой.
находятспектр собственных значений. Например, в случае дискретного спектра – это { F 1, F 2, …, F n, … }. С другой стороны, на эксперименте измеряют физическую величину F и тоже получают ее спектр. Постулат 4 устанавливает связь этой математики квантовой механики с физикой.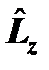 имеют вид:
имеют вид:  ;
; 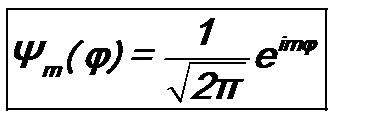 ;
; , скажем, Ψ =
, скажем, Ψ =  , то при измерении физической величины Lz будет получаться только одно значение
, то при измерении физической величины Lz будет получаться только одно значение 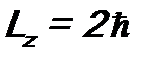 .
. φ n (ξ)
φ n (ξ)
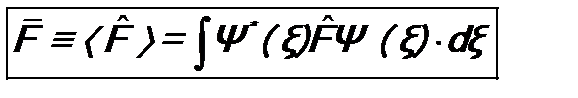 , (8.1),
, (8.1),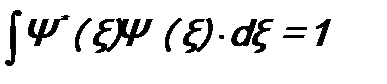 .
. проводится по формуле:
проводится по формуле: . (8.2)
. (8.2) =F n, т.е. равно точному значению из спектра собственных значений.
=F n, т.е. равно точному значению из спектра собственных значений. . (8.3)
. (8.3)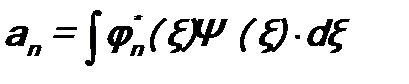 . (8.4)
. (8.4) .
.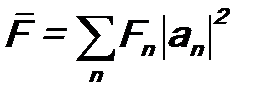 . (8.5)
. (8.5) . (8.6)
. (8.6)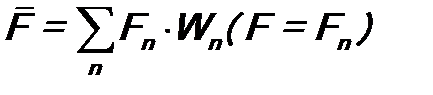 (8.7)
(8.7)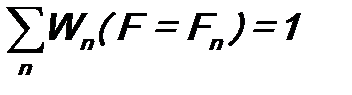 . (8.8)
. (8.8)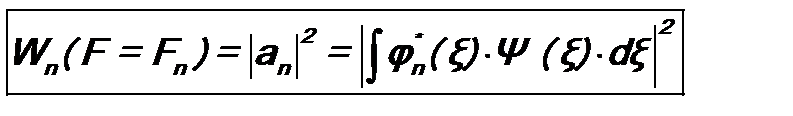 . (8.9)
. (8.9)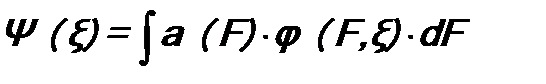

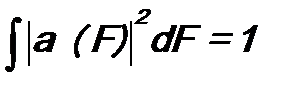 .
.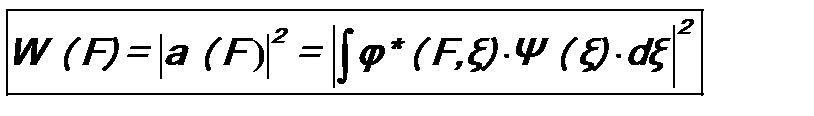 . (8.10)
. (8.10) .
. 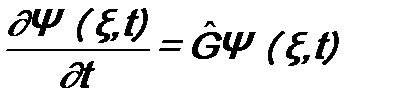 ,
,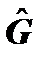 - пока неизвестный нам оператор с размерностью [время]-1, решающий поставленную задачу. Для дальнейшего удобно его переопределить:
- пока неизвестный нам оператор с размерностью [время]-1, решающий поставленную задачу. Для дальнейшего удобно его переопределить: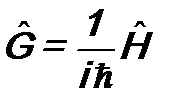 ,
, также пока не известен. Так как размерность постоянной Планка
также пока не известен. Так как размерность постоянной Планка 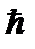 - это [энергия·время], то оператор
- это [энергия·время], то оператор  . (9.1)
. (9.1)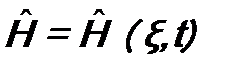 . Про зависимость от пространственной переменной пока ничего не известно, а вот от времени t оператор
. Про зависимость от пространственной переменной пока ничего не известно, а вот от времени t оператор 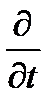 . Но цель уравнения (9.1) как раз и выразить первую производную от волновой функции через саму эту функцию, и с помощью оператора
. Но цель уравнения (9.1) как раз и выразить первую производную от волновой функции через саму эту функцию, и с помощью оператора  не только через Ψ(ξ, t), как требуется, но еще и через нее саму же. Иными словами, оператор
не только через Ψ(ξ, t), как требуется, но еще и через нее саму же. Иными словами, оператор  . Тогда для полного определения состояния системы в момент времени t =0 требуется задать в этот момент времени не только саму волновую функцию Ψ(ξ, t =0), но и ее первую производную
. Тогда для полного определения состояния системы в момент времени t =0 требуется задать в этот момент времени не только саму волновую функцию Ψ(ξ, t =0), но и ее первую производную 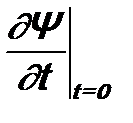 . Это противоречит постулату 1, согласно которому все должна определять только волновая функция Ψ(ξ, t =0). Помимо этой функции, для полного определения состояния системы в момент времени t =0 дополнительно потребуются и другие функции, если в операторе
. Это противоречит постулату 1, согласно которому все должна определять только волновая функция Ψ(ξ, t =0). Помимо этой функции, для полного определения состояния системы в момент времени t =0 дополнительно потребуются и другие функции, если в операторе 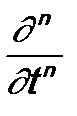 , n =3, 4, … Это опять будет противоречить постулату 1. Аналогичная ситуация будет возникать и тогда, когда в операторе
, n =3, 4, … Это опять будет противоречить постулату 1. Аналогичная ситуация будет возникать и тогда, когда в операторе 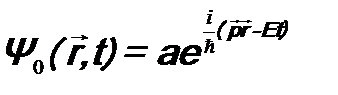 . Будем рассматривать нерелятивистскую задачу, поэтому можно считать:
. Будем рассматривать нерелятивистскую задачу, поэтому можно считать:  . Подставим
. Подставим 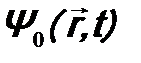 в уравнение (9.1) и подберем так вид оператора
в уравнение (9.1) и подберем так вид оператора  .
. . (9.2)
. (9.2)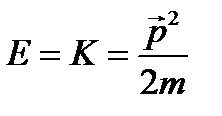 . В соответствии с постулатом 3 оператор кинетической энергии
. В соответствии с постулатом 3 оператор кинетической энергии 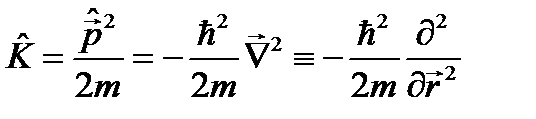
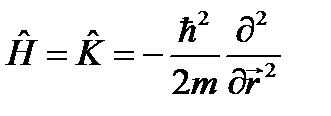 . Подставим этот оператор и функцию
. Подставим этот оператор и функцию 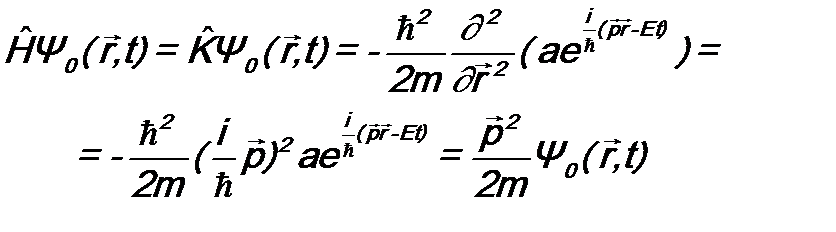 .
.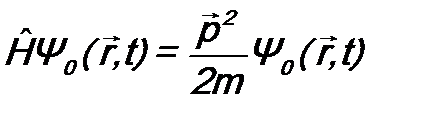 . (9.3)
. (9.3) →
→ 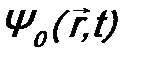 и оператора
и оператора 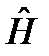 на оператор кинетической энергии
на оператор кинетической энергии 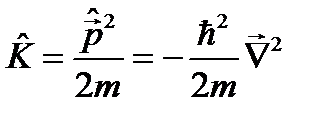 . Иными словами, для свободно движущейся частицы уравнение (9.1) имеет вид:
. Иными словами, для свободно движущейся частицы уравнение (9.1) имеет вид: ; (9.4)
; (9.4) . (9.5)
. (9.5) . Постулируется, что оператор
. Постулируется, что оператор 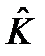 , следует заменить на оператор
, следует заменить на оператор 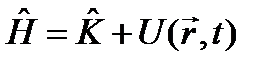 . В итоге для нахождения волновой функции микрочастицы
. В итоге для нахождения волновой функции микрочастицы 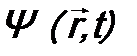 получится уравнение:
получится уравнение: ; (9.6)
; (9.6)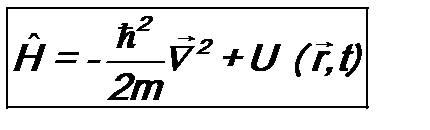 . (9.7)
. (9.7) Э. Шрёдингером и называется: «Уравнение Шрёдингера». Это основное уравнение квантовой механики. Оно позволяет найти волновую функцию микрочастицы, содержащую всю необходимую физическую информацию о ее состоянии. Оператор
Э. Шрёдингером и называется: «Уравнение Шрёдингера». Это основное уравнение квантовой механики. Оно позволяет найти волновую функцию микрочастицы, содержащую всю необходимую физическую информацию о ее состоянии. Оператор 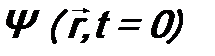 . Для ее нахождения поступают следующим образом. В начальный момент времени t =0 из эксперимента для микрочастицы определяют набор физических величин L, M, N, …, которые одновременно имеют определенные значения. Их число должно быть равно числу степеней свободы у микрочастицы. Можно показать, что соответствующие физические операторы
. Для ее нахождения поступают следующим образом. В начальный момент времени t =0 из эксперимента для микрочастицы определяют набор физических величин L, M, N, …, которые одновременно имеют определенные значения. Их число должно быть равно числу степеней свободы у микрочастицы. Можно показать, что соответствующие физические операторы 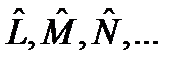 будут коммутировать друг с другом. Как упоминалось в конце лекции 6, операторы такого рода будут иметь общую систему собственных функций. Произведение этих функций и будет определять
будут коммутировать друг с другом. Как упоминалось в конце лекции 6, операторы такого рода будут иметь общую систему собственных функций. Произведение этих функций и будет определять 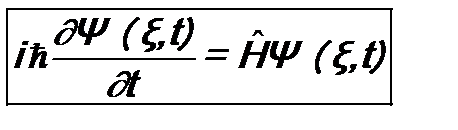 ,
,  ; (9.8)
; (9.8)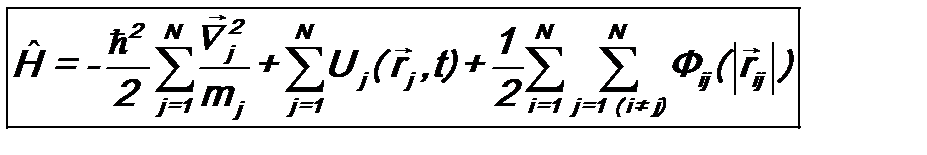 . (9.9)
. (9.9)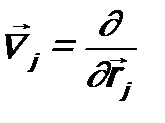 ,
, 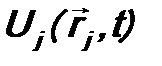 - потенциальная функция, характеризующая силовое поле, которое действует на j -ую частицу,
- потенциальная функция, характеризующая силовое поле, которое действует на j -ую частицу, 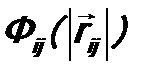 - потенциальная энергия взаимодействия i -ой и j -ой частиц,
- потенциальная энергия взаимодействия i -ой и j -ой частиц, 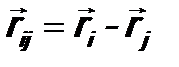 - расстояние между ними.
- расстояние между ними. Лекция 10
Лекция 10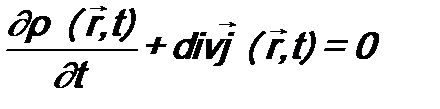 . (10.1)
. (10.1) - плотность частиц в выделенном объеме,
- плотность частиц в выделенном объеме,  - плотность тока частиц,
- плотность тока частиц,  - их скорость. В квантовой механике можно получить аналог уравнения (10.1). Запишем уравнение Шрёдингера и уравнение, комплексно ему сопряженное:
- их скорость. В квантовой механике можно получить аналог уравнения (10.1). Запишем уравнение Шрёдингера и уравнение, комплексно ему сопряженное: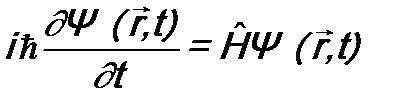 ;
; .
.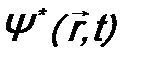 , а второе – на
, а второе – на 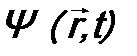 и вычтем одно из другого:
и вычтем одно из другого: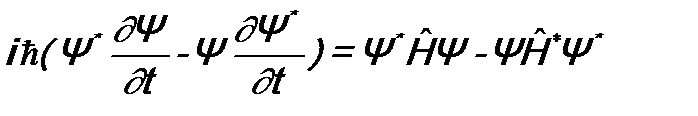 ;
;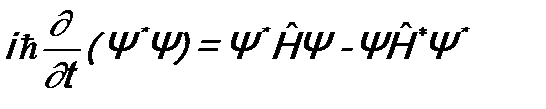 . (10.2)
. (10.2) .
.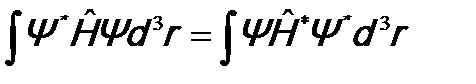
 . (10.3)
. (10.3) - это вероятность обнаружить микрочастицу в точке
- это вероятность обнаружить микрочастицу в точке  в момент времени t. Тогда
в момент времени t. Тогда 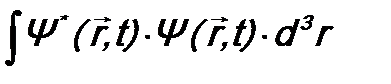 - по теореме сложения вероятностей это будет вероятность того, что микрочастица в момент времени t вообще находится где-то в пространстве. Следовательно, соотношение (10.3) утверждает, что эта вероятность не меняется со временем, т.е. микрочастица не исчезнет.
- по теореме сложения вероятностей это будет вероятность того, что микрочастица в момент времени t вообще находится где-то в пространстве. Следовательно, соотношение (10.3) утверждает, что эта вероятность не меняется со временем, т.е. микрочастица не исчезнет. используется для нормировки волновой функции. Тогда из (10.3) следует, что эта нормировка с течением времени
используется для нормировки волновой функции. Тогда из (10.3) следует, что эта нормировка с течением времени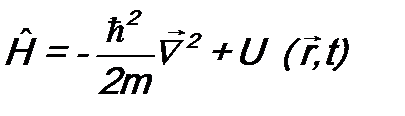 (см. ф-лу (9.7)) и учтем при этом, что из эрмитовости оператора
(см. ф-лу (9.7)) и учтем при этом, что из эрмитовости оператора 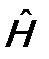 следует:
следует: 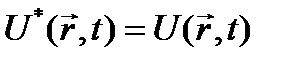 .
. ;
;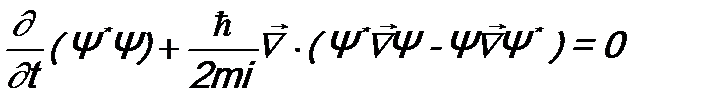 . (10.4)
. (10.4)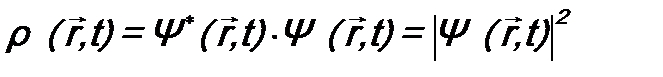 была введена раньше (см. ф-лу (4.3)). Теперь еще определим новую величину
была введена раньше (см. ф-лу (4.3)). Теперь еще определим новую величину , (10.5)
, (10.5)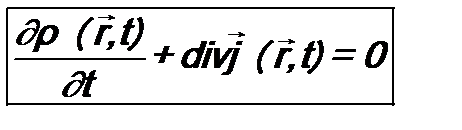 . (10.6)
. (10.6)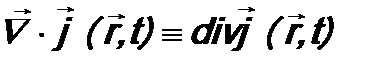 и использовано определение дивергенции вектора
и использовано определение дивергенции вектора  :
: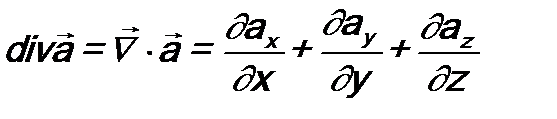 .
. и
и 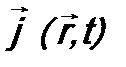 имеют другой смысл. В квантовой механике уравнение (10.6) также можно назвать законом сохранения числа частиц. Согласно ему, изменение плотности вероятности в каком-либо заданном объеме со временем может быть связано только с пространственным изменением (дивергенцией) плотности тока вероятности.
имеют другой смысл. В квантовой механике уравнение (10.6) также можно назвать законом сохранения числа частиц. Согласно ему, изменение плотности вероятности в каком-либо заданном объеме со временем может быть связано только с пространственным изменением (дивергенцией) плотности тока вероятности.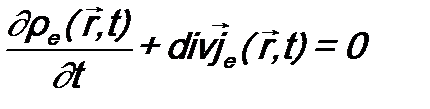 .
.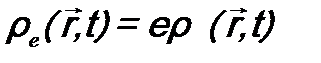 - плотность заряда и
- плотность заряда и 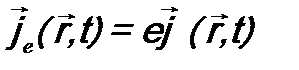 - плотность тока заряда.
- плотность тока заряда.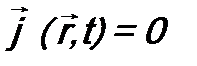 , если волновая функция действительна, т.е.
, если волновая функция действительна, т.е.  .
. 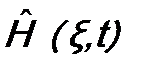 . В нем такая зависимость возникает только через потенциальную функцию
. В нем такая зависимость возникает только через потенциальную функцию 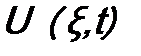 . Если зависимость гамильтониана от времени отсутствует, т.е.
. Если зависимость гамильтониана от времени отсутствует, т.е. 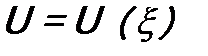 , то волновую функцию находят из уравнения Шредингера для стационарных состояний (часто говорят – из «уравнения Шрёдингера» без слова «временное»).
, то волновую функцию находят из уравнения Шредингера для стационарных состояний (часто говорят – из «уравнения Шрёдингера» без слова «временное»).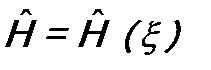 . Тогда в нем можно разделить переменные ξ и t. Имеем:
. Тогда в нем можно разделить переменные ξ и t. Имеем: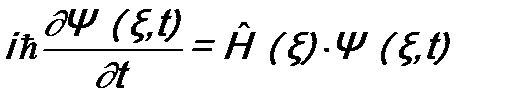 . (11.1)
. (11.1) . (11.2)
. (11.2)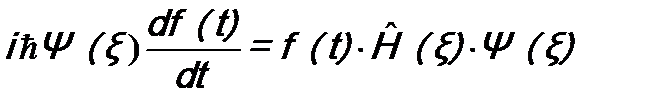 ;
;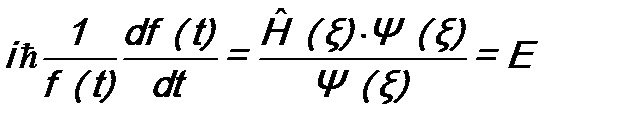 . (11.3)
. (11.3)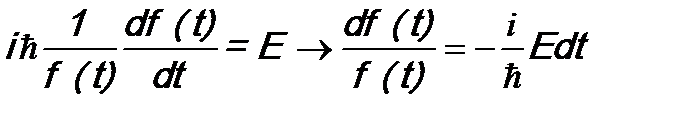 ; (11.4)
; (11.4) . (11.5)
. (11.5)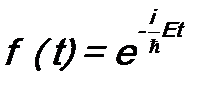 . (11.6)
. (11.6)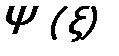 и величину E. Так как гамильтониан от времени не зависит, то, следовательно, в нем вместо потенциальной функции
и величину E. Так как гамильтониан от времени не зависит, то, следовательно, в нем вместо потенциальной функции 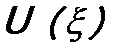 . Это означает, что гамильтониан
. Это означает, что гамильтониан  становится оператором энергии и уравнение (11.5) есть уравнение на его собственные функции и собственные значения. Последние – это энергии соответствующих состояний системы, имеющие определенные значения.
становится оператором энергии и уравнение (11.5) есть уравнение на его собственные функции и собственные значения. Последние – это энергии соответствующих состояний системы, имеющие определенные значения.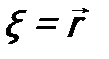 ) это уравнение имеет вид:
) это уравнение имеет вид: , (11.7)
, (11.7)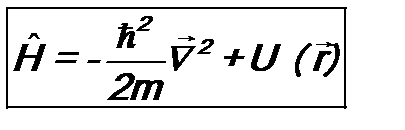 . (11.8)
. (11.8) , так как зависимость от времени полной волновой функции определена ф-лой (11.6). Но в ряде случаев требуется знание именно полной волновой функции стационарного состояния системы, и в соответствии с (11.2) она имеет вид:
, так как зависимость от времени полной волновой функции определена ф-лой (11.6). Но в ряде случаев требуется знание именно полной волновой функции стационарного состояния системы, и в соответствии с (11.2) она имеет вид: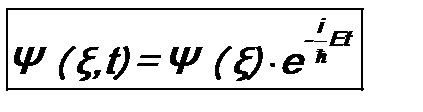 , (11.9)
, (11.9)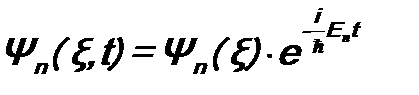 , n = 1, 2, … (11.10)
, n = 1, 2, … (11.10)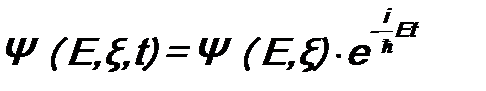 . (11.11)
. (11.11)


