
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
волновая функция должна быть антисимметричнойСодержание книги
Поиск на нашем сайте
по отношению к перестановке любой пары Координат частиц. Все, что говорилось выше о волновой функции системы невзаимодействующих электронов – это частный случай сформулированного выше требования. Так как в бозе-системах принцип Паули не действует, ничто не запрещает частицам накапливаться в одном и том же квантовом состоянии и иметь одинаковые энергии. В итоге могут в квантовой системе бозонов возникать макроскопические эффекты. Например, спрашивается, как возможна, скажем, радиосвязь (или радиотрансляция) на радиоволнах среднего диапазона 300 м? Радиоволна – это электромагнитная волна, состоящая из фотонов. В данном случае энергия фотона исключительно мала – всего 4·10-9 эВ. Никакой радиоприемник такую энергию не зафиксирует. Но фотоны – это бозоны, на них не распространяется действие принципа Паули. Поэтому они могут накапливаться в состоянии с одинаковыми энергиями, складывая их. В результате этой энергии у радиоволны окажется достаточно для передачи физической информации. А вот передать информацию такого рода на электронном пучке будет затруднительно. В системах электронов, как мы видели, действует принцип Паули, из-за которого электроны становятся «индивидуалистами». Это будет им мешать создавать суммарный эффект, как у бозонов. В то же время, скажем в атомах, электроны из-за действия принципа Паули, не «сваливаются» в самое нижнее по энергии состояние, а распределяются по оболочкам с различными энергиями. Примерно тоже имеет место и с нуклонами в атомных ядрах. Из-за всего этого мы знаем атомы и атомные ядра такими, какие они есть, и окружающий нас мир, состоящий атомов, тоже такой, каким он и должен быть. И все это из-за действия принципа Паули в системах ферми-частиц.
Лекция 23 РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА: РЕЛЯТИВИСТСКОЕ УРАВНЕНИЕ ШРЁДИНГЕРА
До настоящего момента рассматривалось нерелятивистское движение микрочастицы, и оно описывалось временным уравнением Шрёдингера. Для свободной частицы оно имело вид:
или Видно, что уравнение (23.1) действительно не может быть релятивистским: в него время t и координата Покажем, как уравнение (23.1) может быть получено полуклассическим способом. Запишем для свободной частицы соотношение между ее энергией и импульсом:
Подставим сюда вместо энергии E оператор энергии в виде
В итоге действительно получилось уравнение (23.1). Как и выше, производим в последнем соотношении замены
Здесь была произведена замена Решение уравнения можно искать в виде волны де Бройля, которая постулировалась как волновая функция свободно движущейся частицы, а нерелятивистская частица или она релятивистская определялось формой зависимости энергии частицы от ее импульса. Итак, ищем волновую функцию Подставив (23.4) в (23.3), получим: Здесь Из (23.6) следует, что у свободно движущейся релятивистской частицы есть два состояния: одно с волновой функцией можно отнести не к энергии Взяв релятивистское уравнение Шрёдингера за основу, найдем состояния электрона в атоме водорода. Для этого необходимо ввести потенциальную энергию электрона в атоме водорода в уравнение (23.3). Запишем его в исходном виде: Если на частицу с электрическим зарядом q действует электрическое поле со скалярным потенциалом φ и векторным потенциалом Как известно, в стационарных состояниях волновая функция ищется в виде:
Это уравнение можно решить точно и получить энергетический спектр и соответствующие волновые функции. Однако, как выяснилось, энергии уровней не соответствуют наблюдаемым. Из этого был сделан вывод, что на основе релятивистского уравнения Шрёдингера нельзя описывать состояния частиц с полуцелым спином, в частности, электрон. Для этого требуется другое уравнение. А с помощью релятивистского уравнения Шрёдингера можно исследовать движение частиц с целочисленным спином. Это уравнение также является основой квантовой теории поля и используется в ней для нахождения полевых характеристик, только в этой теории его называют уравнением Клейна-Гордона.
Лекция 24 РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА: УРАВНЕНИЕ ДИРАКА
Две идеи были основой вывода уравнения Дирака. 1. Уравнение должно иметь Поль Дирак (1902-1984) гамильтонову форму. 2. Его решение но обратное не обязательно. Обсудим эти идеи. 1. Гамильтонова форма уравнения предполагает, что в нем должна быть только первая производная по времени, т.е. уравнение должно иметь вид: где В оператор а мы предположили, что она свободная. Соответственно, раз нет зависимости от координаты, то из-за релятивистской инвариантности искомого уравнения не должно быть и зависимости от времени. Однако мы про эти константы пока ничего не знаем. Поэтому будем исходить из самого общего предположения – это не числа, а матрицы. Такое предположение важно – в произведении порядок расположения чисел можно менять, например, 2. Рассмотрим теперь вторую исходную идею. Ищется уравнение для релятивистской частицы, но в уравнение (24.2) с оператором Выполним эту программу. Запишем уравнение (24.2) в явном виде:
Здесь использовано определение оператора энергии в виде
Использовано алгебраическое соотношение (a+b)(a-b)=a2-b2, где a= При выводе (24.5) учтено, что компоненты оператора импульса коммутируют друг с другом. Для того чтобы (24.5) переходило в уравнение (24.1) и удовлетворяло тем самым требованию 2, от параметров Необходимо также добавить условия эрмитовости: Из соотношений (24.6) видно, что параметры Здесь
В развернутом виде: Если эти матрицы подставить в уравнение Дирака
представить волновую функцию тоже в виде матрицы (функция такого вида называется биспинором) матрицы перемножить, то получится не одно, а 4 связанных дифференциальных уравнения. Их совместное решение даст 4 компоненты волновой функции Но на самом деле, это система 4-х связанных уравнений и волновая функция имеет вид (24.10). Исследование уравнения Дирака в виде (24.11) показывает, что оно, как и релятивистское уравнение Шрёдингера, описывает одновременно и электрон, и его античастицу – позитрон. Но в данном случае в уравнении учтено наличие спинов у электрона и позитрона. Поэтому две компоненты волновой функции (24.10) относятся к электрону (напомним, что спиновые функции двухкомпонентные - спиноры), и две – к позитрону, в итоге получается биспинор. Если уравнение Дирака решается в свернутом виде (24.11), то часто волновую функцию в виде спинора: Одна из этих функций относится к электрону, а другая – к позитрону. Уравнение Дирака легко обобщается на случай, когда на частицу действует поле и она имеет потенциальную энергию Положив здесь Как и следовало ожидать, получается нерелятивистское уравнение Шрёдингера с поправками порядка
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.132 (0.009 с.) |

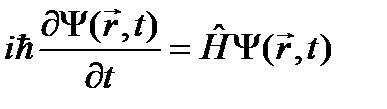 ,
, 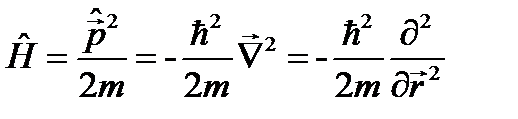
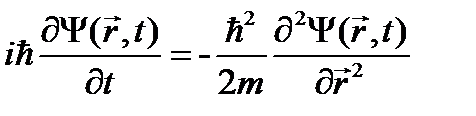 . (23.1)
. (23.1)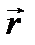 входят не одинаково - производные по времени и по координате имеют различный порядок. Как известно, преобразование Лоренца для релятивистских уравнений требует равноправности координаты и времени.
входят не одинаково - производные по времени и по координате имеют различный порядок. Как известно, преобразование Лоренца для релятивистских уравнений требует равноправности координаты и времени.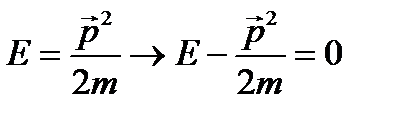 .
.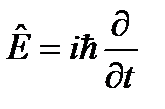 (см. разд. 1 в лекции 14) и вместо импульса
(см. разд. 1 в лекции 14) и вместо импульса 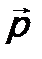 оператор импульса
оператор импульса 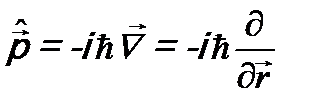 . После этого получившимся оператором подействуем на волновую функцию
. После этого получившимся оператором подействуем на волновую функцию 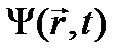 и результат приравняем нулю (в соответствии с постулатом 3 (см. лекцию 7)):
и результат приравняем нулю (в соответствии с постулатом 3 (см. лекцию 7)):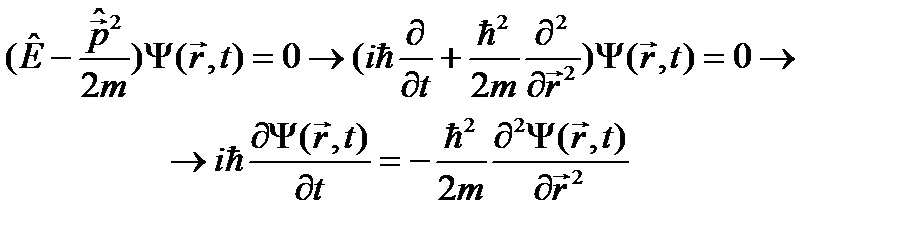 .
.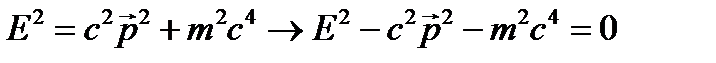 . (23.2)
. (23.2) и
и 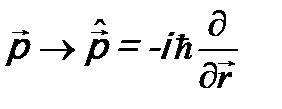 , получившимся оператором действуем на волновую функцию
, получившимся оператором действуем на волновую функцию 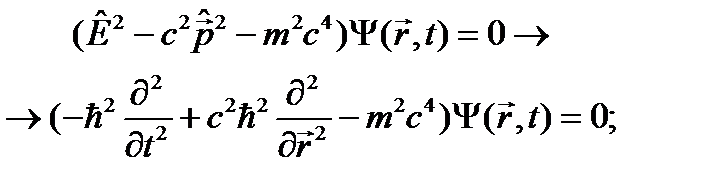
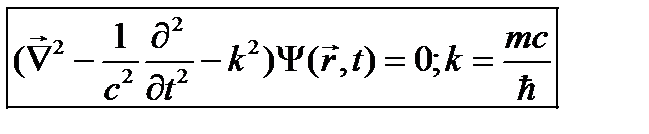 . (23.3)
. (23.3)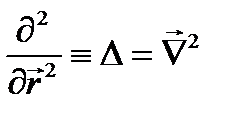 . Уравнение (23.3) и есть релятивистское уравнение Шрёдингера для свободно движущейся частицы. Как и должно быть, в него время t и координата
. Уравнение (23.3) и есть релятивистское уравнение Шрёдингера для свободно движущейся частицы. Как и должно быть, в него время t и координата  . (23.4)
. (23.4)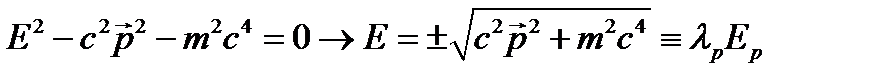 . (23.5)
. (23.5)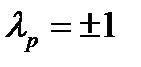 и
и 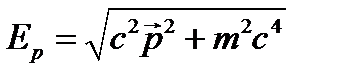 . В итоге
. В итоге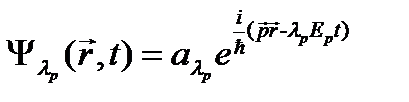 . (23.6)
. (23.6)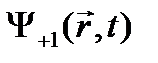 и с энергией
и с энергией 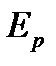 , а другое - с волновой функцией
, а другое - с волновой функцией 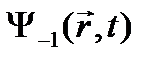 и с энергией
и с энергией  . Последнее обстоятельство не было понятно: как у свободной частицы, обладающей только кинетической энергией, эта энергия может быть отрицательной? Для разрешения этого противоречия было сделано предположение, что релятивистское уравнение Шрёдингера одновременно описывает состояния двух частиц – частицы и античастицы, например, электрона и позитрона, и их разорвать невозможно. Отрицательный знак у энергии
. Последнее обстоятельство не было понятно: как у свободной частицы, обладающей только кинетической энергией, эта энергия может быть отрицательной? Для разрешения этого противоречия было сделано предположение, что релятивистское уравнение Шрёдингера одновременно описывает состояния двух частиц – частицы и античастицы, например, электрона и позитрона, и их разорвать невозможно. Отрицательный знак у энергии 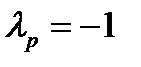
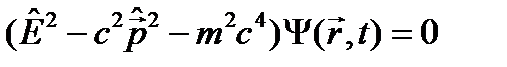 . (23.7)
. (23.7)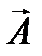 , то в уравнении (23.7) следует сделать замены:
, то в уравнении (23.7) следует сделать замены: 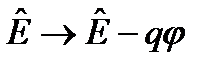 и
и 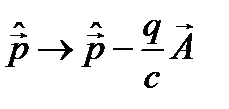 (см. лекцию 19). В нашем случае q =- e,
(см. лекцию 19). В нашем случае q =- e, 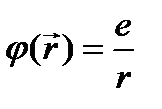 - кулоновское поле точечного заряда ядра, т.е. протона, и
- кулоновское поле точечного заряда ядра, т.е. протона, и 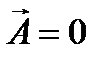 . В результате релятивистское уравнение Шрёдингера (23.7) принимает вид:
. В результате релятивистское уравнение Шрёдингера (23.7) принимает вид: . (23.8)
. (23.8) 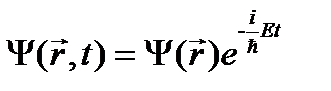 . (23.9)
. (23.9)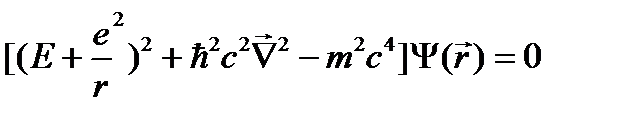 .
.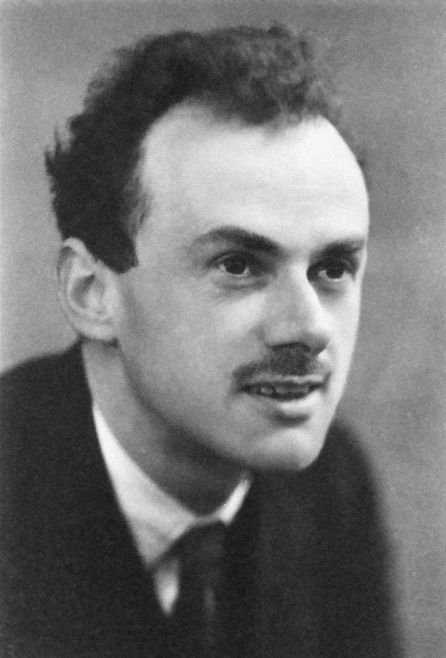 В 1928 г. П. Дирак получил релятивистское уравнение – уравнение Дирака, пригодное для частиц с полуцелым спином, в частности, для электронов. На его основе он предсказал существование античастиц. Для электрона античастица – это позитрон, его открыл в 1932 г. американский физик-экспериментатор К. Андерсен, подтвердив предсказание П.Дирака.
В 1928 г. П. Дирак получил релятивистское уравнение – уравнение Дирака, пригодное для частиц с полуцелым спином, в частности, для электронов. На его основе он предсказал существование античастиц. Для электрона античастица – это позитрон, его открыл в 1932 г. американский физик-экспериментатор К. Андерсен, подтвердив предсказание П.Дирака.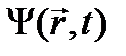 должно удовлетворять релятивистскому уравнению Шрёдингера
должно удовлетворять релятивистскому уравнению Шрёдингера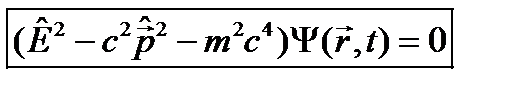 , (24.1)
, (24.1)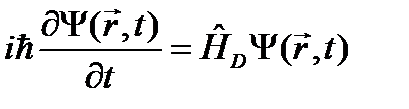 , (24.2)
, (24.2)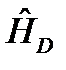 - это пока неизвестный оператор с размерностью энергии. Будем рассматривать свободное движение частицы. Можно из общих соображений предположить, каким должен быть оператор
- это пока неизвестный оператор с размерностью энергии. Будем рассматривать свободное движение частицы. Можно из общих соображений предположить, каким должен быть оператор 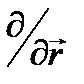 . Такой физический оператор в квантовой механике есть – это оператор импульса
. Такой физический оператор в квантовой механике есть – это оператор импульса 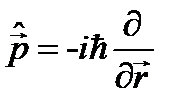 . Следовательно, в операторе
. Следовательно, в операторе 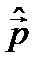 , причем в первой степени, а не в квадрате, как в уравнении Шрёдингера. Оператор
, причем в первой степени, а не в квадрате, как в уравнении Шрёдингера. Оператор 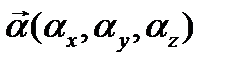 . Иными словами, в операторе
. Иными словами, в операторе 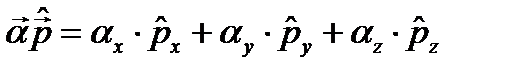 . Но это слагаемое имеет размерность импульса, а не энергии, поэтому следует его умножить на скорость света c (см., например, (23.2)). В итоге будет оператор
. Но это слагаемое имеет размерность импульса, а не энергии, поэтому следует его умножить на скорость света c (см., например, (23.2)). В итоге будет оператор 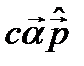 . К нему можно с безразмерным коэффициентом β добавить еще один скаляр с размерностью энергии – это
. К нему можно с безразмерным коэффициентом β добавить еще один скаляр с размерностью энергии – это 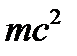 , где m – масса электрона. Таким образом, получается:
, где m – масса электрона. Таким образом, получается: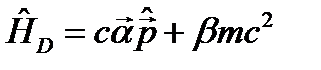 . (24.3)
. (24.3)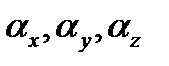 и β. Они должны быть константами, т.е. не зависеть ни от t, ни от
и β. Они должны быть константами, т.е. не зависеть ни от t, ни от 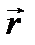 . Последняя зависимость, по сути, физически означала бы действие каких-то полей на частицу,
. Последняя зависимость, по сути, физически означала бы действие каких-то полей на частицу,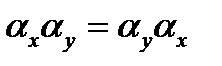 , а матричная алгебра в общем случае некоммутативная, т.е.
, а матричная алгебра в общем случае некоммутативная, т.е.  . Это означает, что при перемножении матриц надо следить за порядком их расположения в произведении.
. Это означает, что при перемножении матриц надо следить за порядком их расположения в произведении.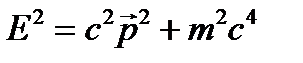 . Поэтому исходное требование 2, по сути, означает, что и в решение уравнения (24.2) будет также заложен релятивизм. Кроме того, это требование предлагает и путь, на котором можно выяснить, какими должны быть матрицы
. Поэтому исходное требование 2, по сути, означает, что и в решение уравнения (24.2) будет также заложен релятивизм. Кроме того, это требование предлагает и путь, на котором можно выяснить, какими должны быть матрицы 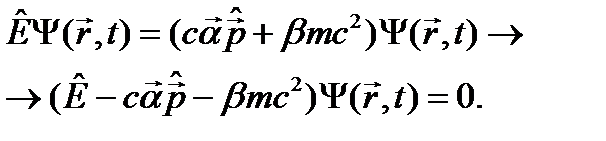
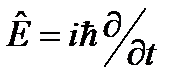 . Умножим последнее уравнение на оператор
. Умножим последнее уравнение на оператор 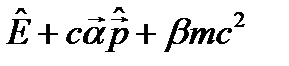 (равенство нулю, конечно, останется):
(равенство нулю, конечно, останется):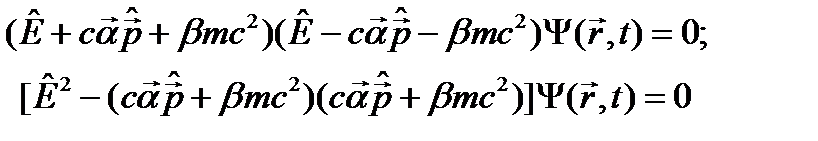 . (24.4)
. (24.4)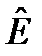 и b=
и b= 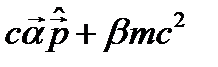 . Это возможно, так как операторы
. Это возможно, так как операторы 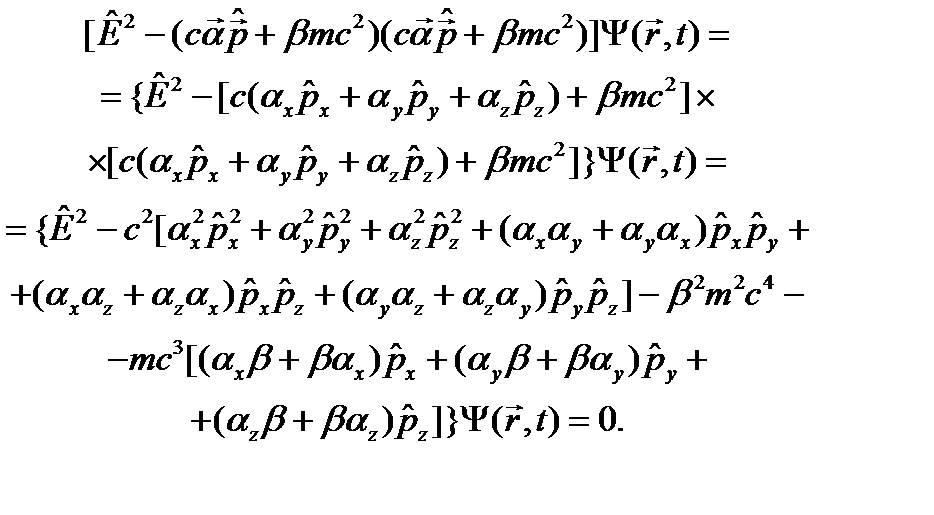 (24.5)
(24.5)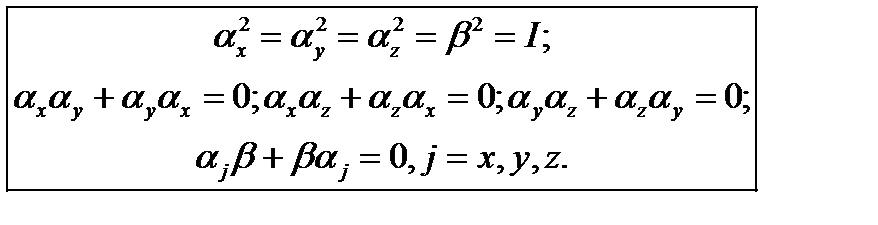 (24.6)
(24.6)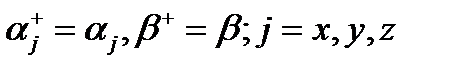 . (24.7)
. (24.7)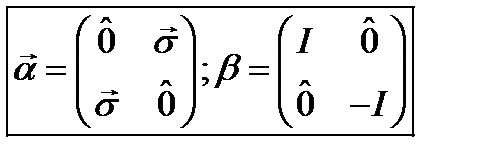 . (24.8)
. (24.8)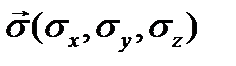 - матрицы Паули
- матрицы Паули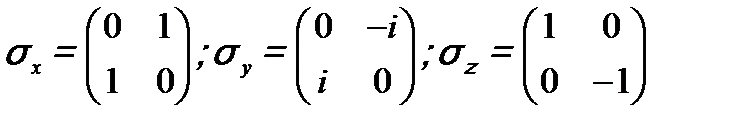 ;
;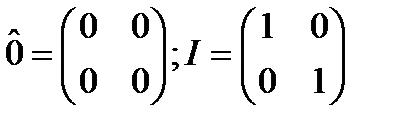 .
.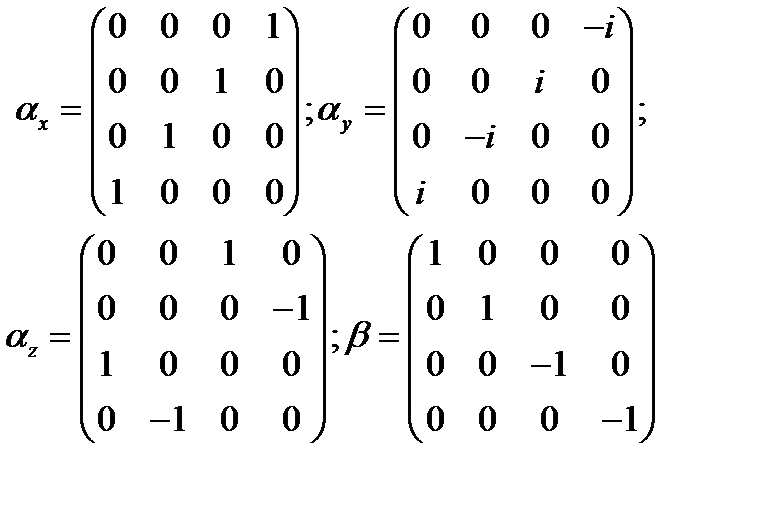 . (24.9)
. (24.9) 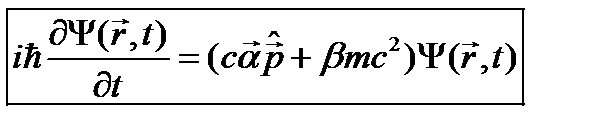 ,
,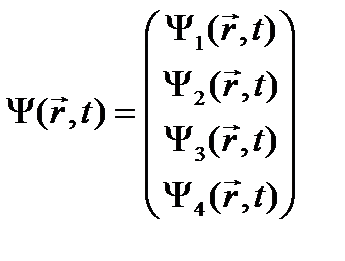 (24.10)
(24.10)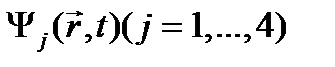 и энергетический спектр, если рассматриваются стационарные состояния. Итак, формально уравнение Дирака можно представить в виде:
и энергетический спектр, если рассматриваются стационарные состояния. Итак, формально уравнение Дирака можно представить в виде: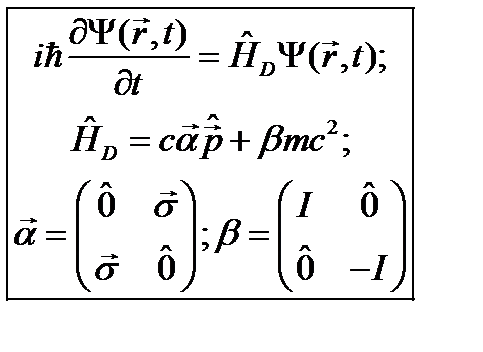 . (24.11)
. (24.11)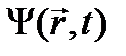 формально представляют
формально представляют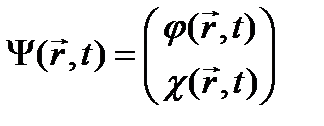 . (24.12)
. (24.12) . В этом случае
. В этом случае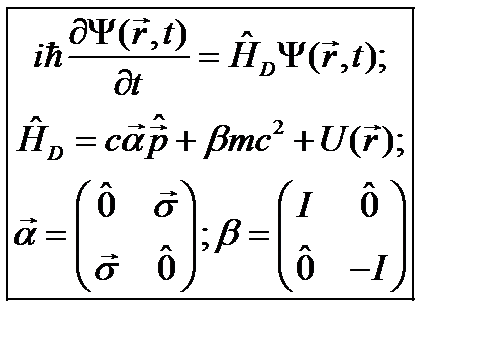 . (24.13)
. (24.13) , можно получить энергетический спектр и соответствующие волновые функции для водородоподобного атома. Задача решается точно, как и в нерелятивистском случае, но спектр энергий лучше согласуется с экспериментальным. В частности, воспроизводится и дублетная структура уровней у водородоподобного атома, обусловленная наличием спина у электрона и спин-орбитальным взаимодействием. Точный вид последнего можно получить, выполнив в уравнении Дирака в виде (24.13) предельный переход к нерелятивистскому случаю, когда скорость электрона
, можно получить энергетический спектр и соответствующие волновые функции для водородоподобного атома. Задача решается точно, как и в нерелятивистском случае, но спектр энергий лучше согласуется с экспериментальным. В частности, воспроизводится и дублетная структура уровней у водородоподобного атома, обусловленная наличием спина у электрона и спин-орбитальным взаимодействием. Точный вид последнего можно получить, выполнив в уравнении Дирака в виде (24.13) предельный переход к нерелятивистскому случаю, когда скорость электрона  .
.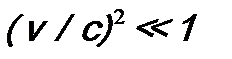 к оператору кинетической энергии и с добавкой к потенциальной энергии электрона
к оператору кинетической энергии и с добавкой к потенциальной энергии электрона 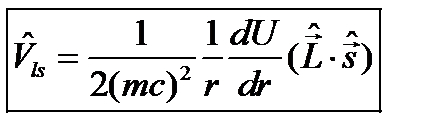 . Наличие в нем оператора спина
. Наличие в нем оператора спина 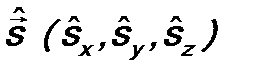 непосредственно свидетельствует, что, как уже говорилось выше, в самой структуре уравнения Дирака спин у электрона учитывается. В это уравнение его не надо вводить искусственно, как это делается в уравнении Шрёдингера.
непосредственно свидетельствует, что, как уже говорилось выше, в самой структуре уравнения Дирака спин у электрона учитывается. В это уравнение его не надо вводить искусственно, как это делается в уравнении Шрёдингера. 


