
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства собственных функцийСодержание книги
Поиск на нашем сайте
Определение: две функции φ 1(ξ) и φ 2(ξ) называются ортогональными, если для них выполняется соотношение:
а). Случай дискретного спектра.
1. Собственные функции, принадлежащие различным собственным значениям эрмитового оператора, ортогональны. Докажем. Пусть собственная функция φ n (ξ) принадлежит собственному значению Fn, а собственная функция φ m (ξ) → Fm, причем Fn
Во втором уравнении учтено, что Fm = Fm *, как было доказано выше. Проинтегрируем эти равенства по всему пространству и вычтем одно из другого.
Из условия эрмитовости оператора Тогда Так как по условию Fn что и требовалось доказать. Обычно собственные функции оператора нормируют. Поэтому Объединяя условия (c) и (d) в одно, получим условие ортонормировки собственных функций: Здесь Аналогично условие ортонормировки можно записать и для собственных функций оператора с вырожденным спектром (см. (5.10) ):
2. Система собственных функций линейного эрмитового оператора полная. Это свойство означает, что произвольную функцию Ψ (ξ), удовлетворяющую стандартным условиям, можно разложить в ряд по собственным функциям линейного эрмитового оператора φ n (ξ): Коэффициенты разложения an можно найти, умножив соотношение (6.3) на φ m * (ξ) и проинтегрировав по ξ:
Здесь было использовано условие ортонормировки собственных функций (6.1) и определение символа Кронекера (6.2). Таким образом, Если функция Ψ (ξ) нормирована, то, подставив в условие ее нормировки разложение (6.3), можно для коэффициентов an получить критерий полноты разложения (6.3): 3. Условие полноты системы собственных функций Здесь ξ и ξ’ – две пространственных точки. δ (ξ) – дельта-функция Дирака. Поскольку она часто используется в квантовой механике, отметим некоторые ее свойства. 1.
2. Точки a и b задают интервал интегрирования [ a, b ]. 3.
4. 5. 6. 7. 8.
б). Случай непрерывного спектра.
1. Собственные функции, принадлежащие различным собственным значениям эрмитового оператора, ортогональны: Если Причина – нельзя в непрерывном спектре брать точное значение F, необходимо рассматривать бесконечно малый интервал значений F, F + dF. При этом собственную функцию
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.29 (0.009 с.) |

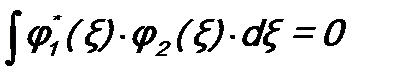 .
.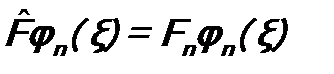
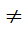 Fm.
Fm.  Это означает, что удовлетворяются уравнения:
Это означает, что удовлетворяются уравнения: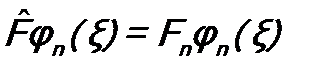 , (a)
, (a)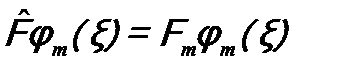 . (b)
. (b)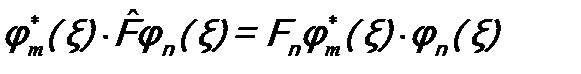 ;
;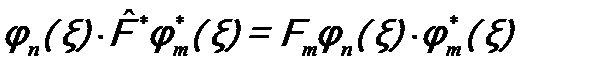 .
.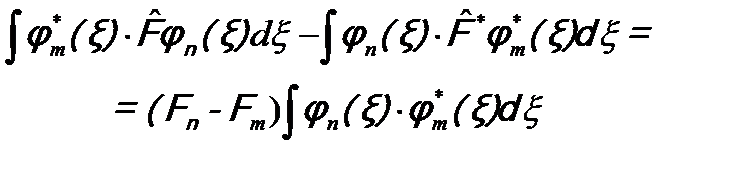 .
.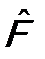 (см. (5.7)) следует:
(см. (5.7)) следует: 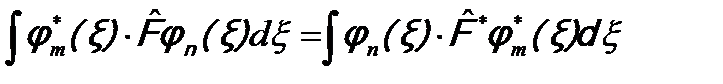 .
.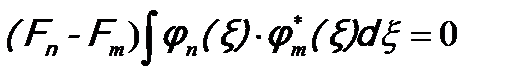 .
.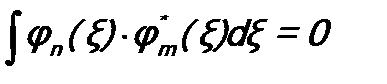 , (c)
, (c)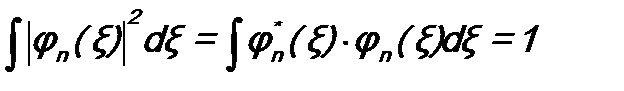 . (d)
. (d)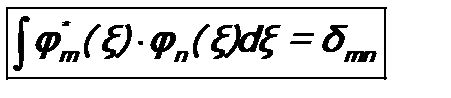 . (6.1)
. (6.1) - символ Кронекера:
- символ Кронекера: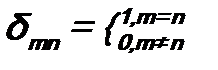 . (6.2)
. (6.2)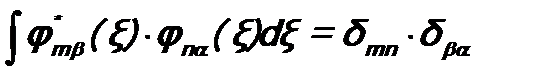 .
.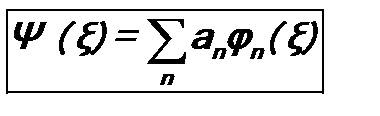 . (6.3)
. (6.3)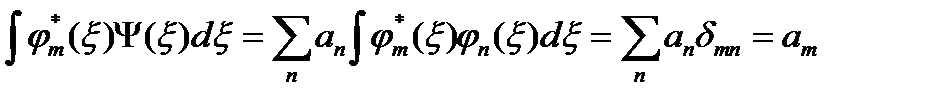 .
.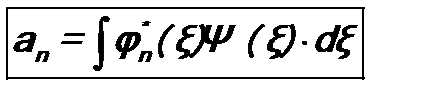 . (6.4)
. (6.4)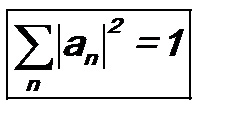 . (6.5)
. (6.5) 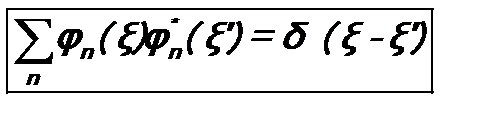 . (6.6)
. (6.6)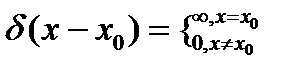 ;
;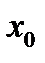 - фиксированная координата в пространстве.
- фиксированная координата в пространстве.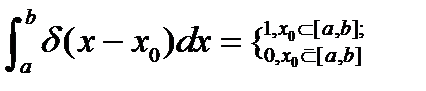 .
.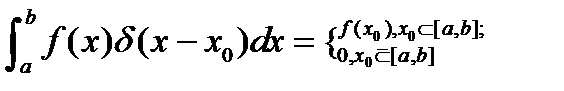 .
.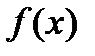 - произвольная функция.
- произвольная функция.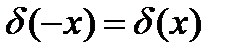 .
.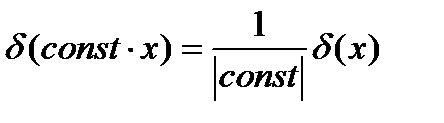 .
.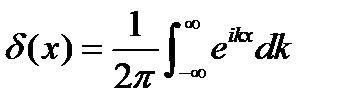 ;
; .
.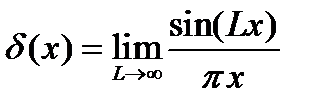 ;
; 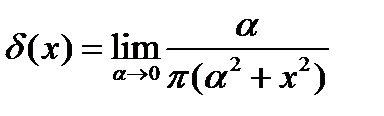 .
.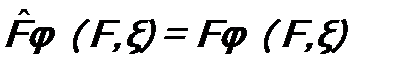 .
.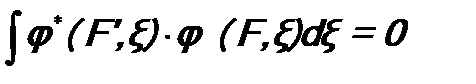 . (6.7)
. (6.7) 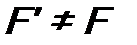 .
.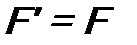 , то для собственных функций
, то для собственных функций 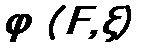 будет условие нормировки. Однако возникает проблема – нормировочный интеграл расходится.
будет условие нормировки. Однако возникает проблема – нормировочный интеграл расходится.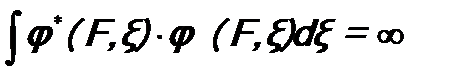 . (6.8)
. (6.8)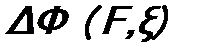 :
: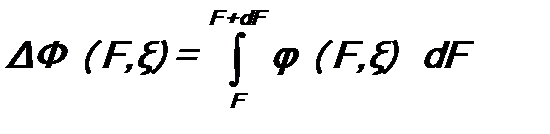 .
.


