
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства стационарных состоянийСодержание книги
Поиск на нашем сайте
1. Волновые функции в виде (11.10) или (11.11) образуют полную систему, т.е. допускают разложение произвольной функции
если спектр энергий дискретный, и
если спектр энергий непрерывный.
2. Плотность вероятности По определению (см. (4.3)) и с учетом (11.9) получаем:
что и требовалось доказать. Аналогично с использованием формул (10.5) и (11.9) (в этом случае ξ = 3. Среднее значение физической величины от времени не зависит. Если микросистема находится в состоянии с волновой функцией
Подстановка в это выражение волновой функции в виде (11.9) дает утверждаемое выше:
4. Вероятность результата измерения физической величины не изменяется с течением времени. Пусть микросистема находится в стационарном состоянии
что и требовалось доказать.
Лекция 12 СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
Предположим, что нас интересуют две физических величины F и G, например, Lz и или Lx и Ly и пр. Соответственно предполагается, что известны их операторы Оператор Если известно состояние микрочастицы, т.е. ее волновая функция
Можно ввести операторы отклонения от среднего значения: С помощью операторов
Именно они используются для количественной характеристики разброса, т.е. неопределенности, значений физических величин F и G при их экспериментальном измерении. Если, например,
Получим это соотношение. Пусть есть три линейных эрмитовых оператора или Введем очевидное неравенство: Здесь α = α *). Очевидность неравенства (12.4) в том, что под знаком интеграла стоит всюду неотрицательная величина, а потому и сам интеграл будет неотрицательным. Раскроем неравенство (12.4):
Здесь для подчеркнутых операторов были использованы их свойства эрмитовости (см. (5.6)), определение среднего значения (см. (8.1), знак Итак, получено: Функция y (α) имеет вид параболы и, если ее нарисовать в плоскости (α, y), то ни при каких значениях α она не должна пересекать ось абсцисс (
Отсюда следует, что, если
действительных корней либо не будет (знак “>”), либо они будут совпадать (знак “=”). Соответственно, полагая Операторы Из него следует, что среднеквадратичные значения физических величин
В классической физике такого не бывает! Рассмотрим частный случай соотношения неопределенностей (12.7), положив F = x и G = px. Поскольку коммутатор Это соотношение неопределенностей Гейзенберга, полученное им в 1925 г. Иногда его записывают в упрощенном виде:
то Δ x →
Дифракция электронов на одной щели.
Соотношение неопределенностей утверждает, что для характеристики состояния микрочастицы нельзя использовать физические величины из классической физики, если их операторы не коммутируют. Для этой цели следует применять только те из них, которые являются интегралами состояния.
Лекция 13 ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАТОРОВ ПО ВРЕМЕНИ И ИНТЕГРАЛЫ СОСТОЯНИЯ КВАНТОВОЙ СИСТЕМЫ
Предположим, что оператор физической величины действует не только на координаты микрочастиц ξ, но еще зависит и от времени t, т.е. Продифференцируем это соотношение по времени:
Для удобства в последнем интеграле производная Подставим сюда производные (
Введем оператор Здесь Сравнивая (13.2) и (13.3), получаем: Это соотношение позволяет вычислять величину Если среднее значение физической величины 1. 2. Для физических операторов
Лекция 14 СВОЙСТВА ПРОСТРАНСТВА-ВРЕМЕНИ И ИНТЕГРАЛЫ СОСТОЯНИЯ КВАНТОВОЙ СИСТЕМЫ: ЭНЕРГИЯ И ИМПУЛЬС
В классической механике показывается, что существование интегралов движения у частицы или системы частиц есть следствие однородности времени и однородности или изотропии пространства. Аналогичное положение имеет место и в квантовой механике, и это позволяет получить вид операторов тех физических величин, которые являются интегралами состояния микросистемы.
|
|||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.85.225 (0.009 с.) |

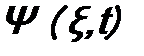 :
: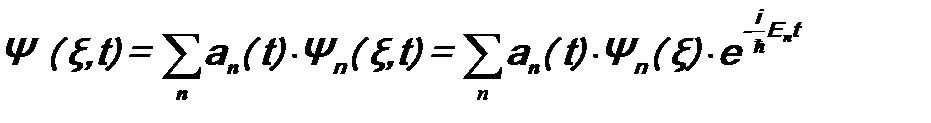 ,
, ,
,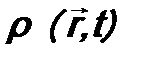 и плотность тока вероятности
и плотность тока вероятности 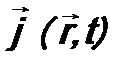 не изменяются с течением времени.
не изменяются с течением времени.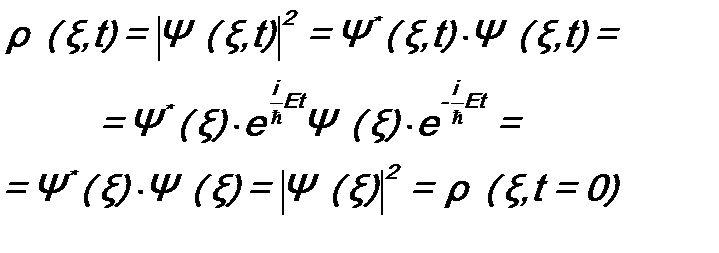 ,
,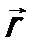 ) доказывается, что
) доказывается, что 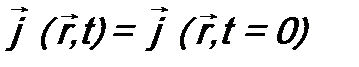 .
.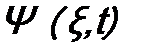 , то по определению (8.1) среднее значение физической величины F
, то по определению (8.1) среднее значение физической величины F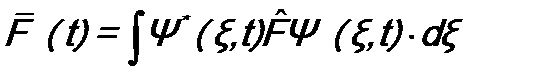 .
.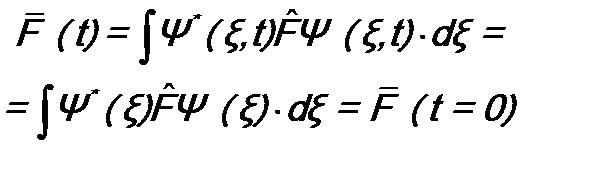 .
.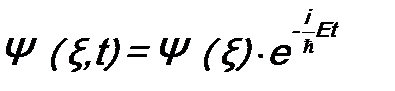 . Рассмотрим, например, физическую величину F с дискретным спектром. Тогда вероятность того, что F = Fn, будет (см. (8.9)):
. Рассмотрим, например, физическую величину F с дискретным спектром. Тогда вероятность того, что F = Fn, будет (см. (8.9)):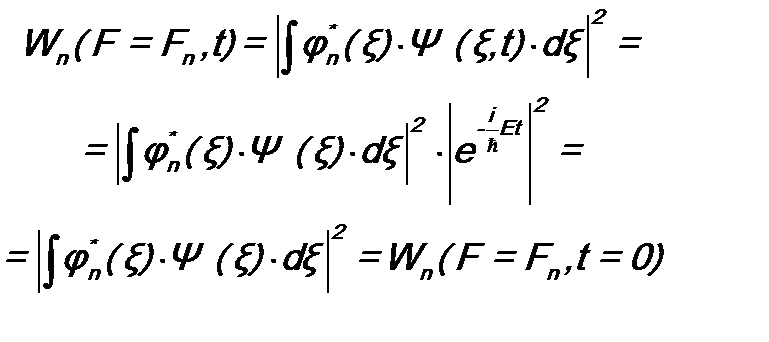 ,
,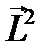 , или x и px,
, или x и px,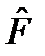 и
и 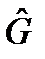 , а также коммутатор
, а также коммутатор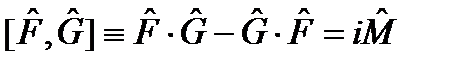 . (12.1)
. (12.1)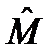 может быть любым - нулем (тогда операторы
может быть любым - нулем (тогда операторы 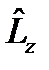 и
и 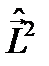 коммутируют и
коммутируют и 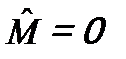 , для операторов x и
, для операторов x и 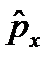
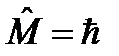 , а для операторов
, а для операторов 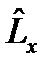 и
и 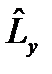
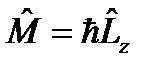 .
.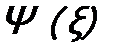 (включать в аргумент время не будем), то можно будет вычислить средние значения
(включать в аргумент время не будем), то можно будет вычислить средние значения 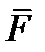 и
и 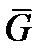 по формуле (8.1):
по формуле (8.1):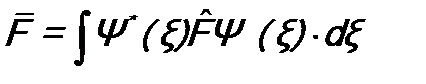 ;
;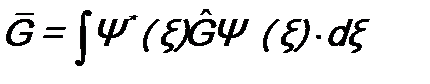 .
.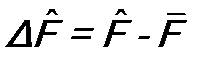 и
и 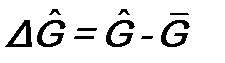 . Так как средние значения
. Так как средние значения 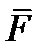 и
и 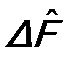 и
и 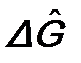 будет таким же, как и операторов
будет таким же, как и операторов 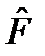 и
и 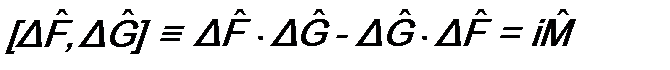 . (12.2)
. (12.2)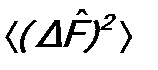 и
и 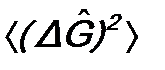 для физических величин F и G:
для физических величин F и G: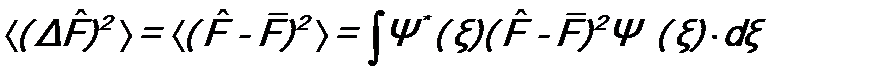 ;
;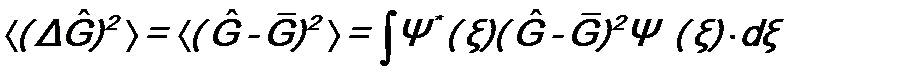 .
.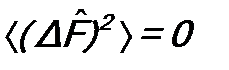 , то разброс отсутствует и величина F имеет вполне определенное значение. В классической физике величины
, то разброс отсутствует и величина F имеет вполне определенное значение. В классической физике величины 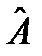 ,
, 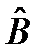 и
и 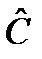 , и они связаны коммутационным соотношением
, и они связаны коммутационным соотношением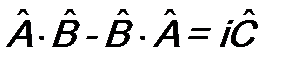 , (12.3)
, (12.3)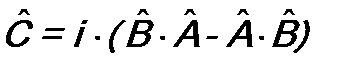 . (12.3*)
. (12.3*)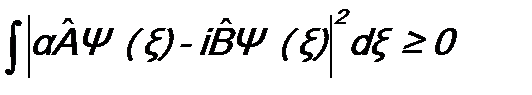 . (12.4)
. (12.4)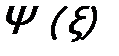 - волновая функция микрочастицы (время включать в аргумент не будем), α – произвольный параметр (будем считать его действительным, т.е.
- волновая функция микрочастицы (время включать в аргумент не будем), α – произвольный параметр (будем считать его действительным, т.е.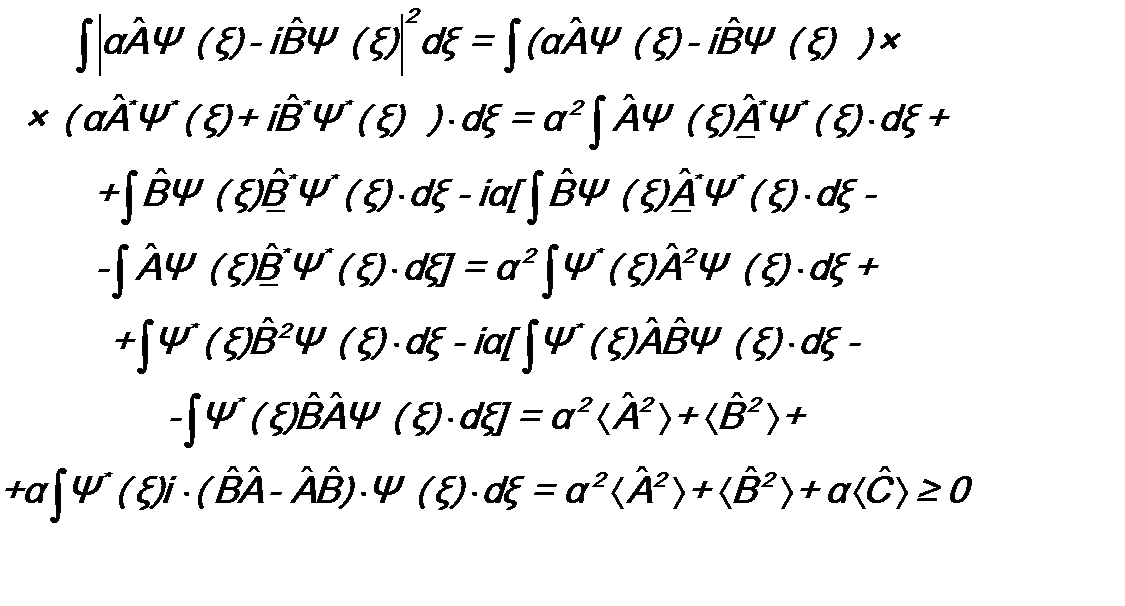 .
.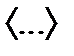 означает усреднение), а также соотношение (12.3*).
означает усреднение), а также соотношение (12.3*).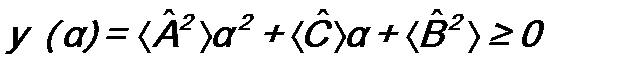 . (12.5)
. (12.5)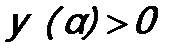 ), но может ее касаться сверху (
), но может ее касаться сверху (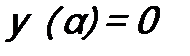 ). Иными словами, квадратное уравнение по параметру α, т.е. уравнение
). Иными словами, квадратное уравнение по параметру α, т.е. уравнение 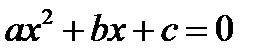 имеют вид:
имеют вид: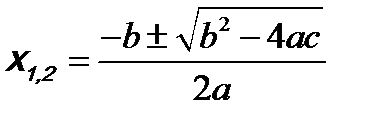 .
.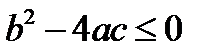 →
→ 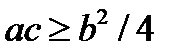 ,
,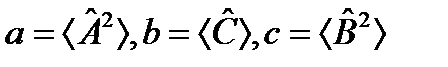 , получаем условие выполнения соотношения (12.5):
, получаем условие выполнения соотношения (12.5):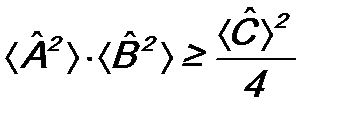 . (12.6)
. (12.6)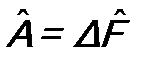 ,
, 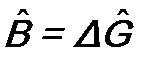 и
и 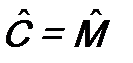 . Подставляя их в (12.6), получаем соотношение неопределенностей для физических величин F и G:
. Подставляя их в (12.6), получаем соотношение неопределенностей для физических величин F и G: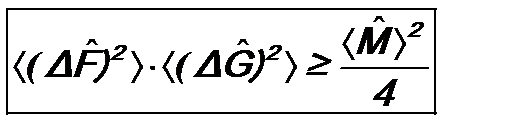 . (12.7)
. (12.7)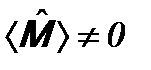 . Более того, если, например, величина
. Более того, если, например, величина  , т.е. F имеет определенное значение, то
, т.е. F имеет определенное значение, то 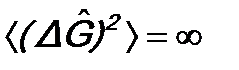 , т.е. G не будет иметь определенного значения. И, наоборот, если
, т.е. G не будет иметь определенного значения. И, наоборот, если 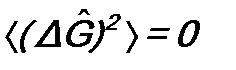 , то
, то 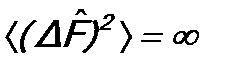 , и физическая величина F не будет иметь определенного значения.
, и физическая величина F не будет иметь определенного значения.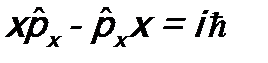 , то
, то 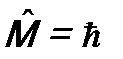 и
и 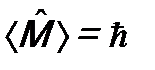 . Соотношение неопределенностей (12.7) тогда принимает вид:
. Соотношение неопределенностей (12.7) тогда принимает вид: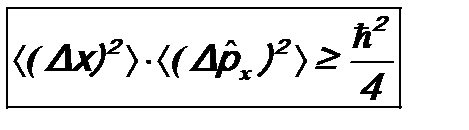 . (12.8)
. (12.8)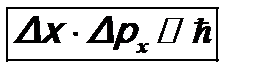 , (12.9)
, (12.9)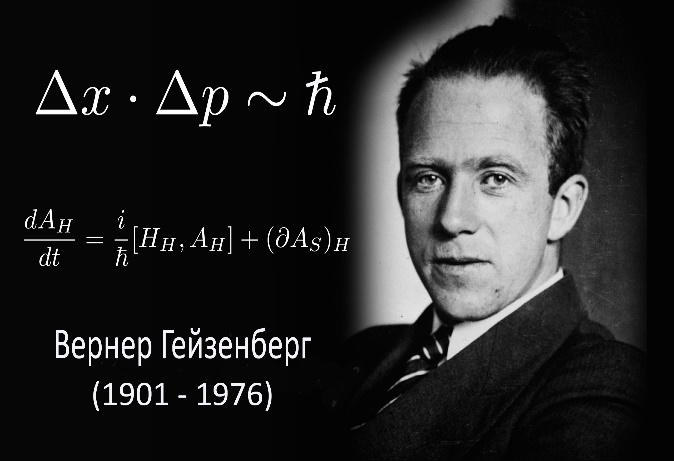 подразумевая под величинами Δ x и Δpx неточности в значениях координаты x и проекции импульса px на ось x при их экспериментальном измерении у микрочастицы. Из (12.9) прямо следует, что у микрочастицы понятие траектории отсутствует в классическом ее понимании. Действительно, движение частицы по траектории означает, что в любой момент времени для точно заданной координаты x можно указать точное значение проекции импульса px и наоборот. А из соотношения (12.9) следует, что чем точнее измеряется координата, т.е. Δ x →0, тем неопределеннее будет проекция импульса, так как Δpx →
подразумевая под величинами Δ x и Δpx неточности в значениях координаты x и проекции импульса px на ось x при их экспериментальном измерении у микрочастицы. Из (12.9) прямо следует, что у микрочастицы понятие траектории отсутствует в классическом ее понимании. Действительно, движение частицы по траектории означает, что в любой момент времени для точно заданной координаты x можно указать точное значение проекции импульса px и наоборот. А из соотношения (12.9) следует, что чем точнее измеряется координата, т.е. Δ x →0, тем неопределеннее будет проекция импульса, так как Δpx → 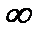 . И, наоборот, если Δpx →0,
. И, наоборот, если Δpx →0,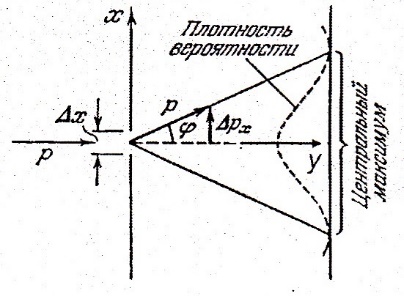
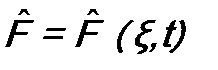 . Если известна волновая функция системы Ψ(ξ, t), можно вычислить среднее значение
. Если известна волновая функция системы Ψ(ξ, t), можно вычислить среднее значение 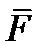 :
: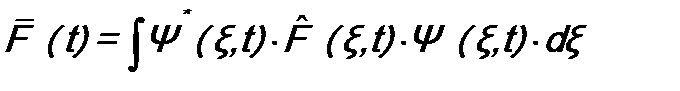 . (13.1)
. (13.1)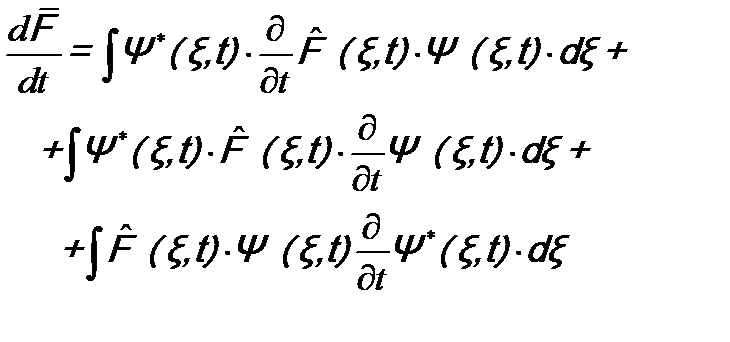 .
.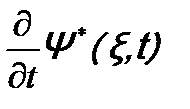 переставлена с функцией
переставлена с функцией 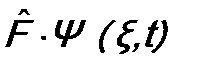 .
.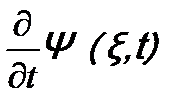 и
и 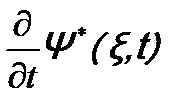 , взяв их из временного уравнения Шрёдингера
, взяв их из временного уравнения Шрёдингера 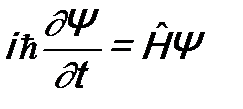
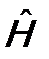 - гамильтониан):
- гамильтониан):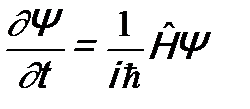 ;
; 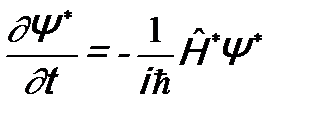 .
.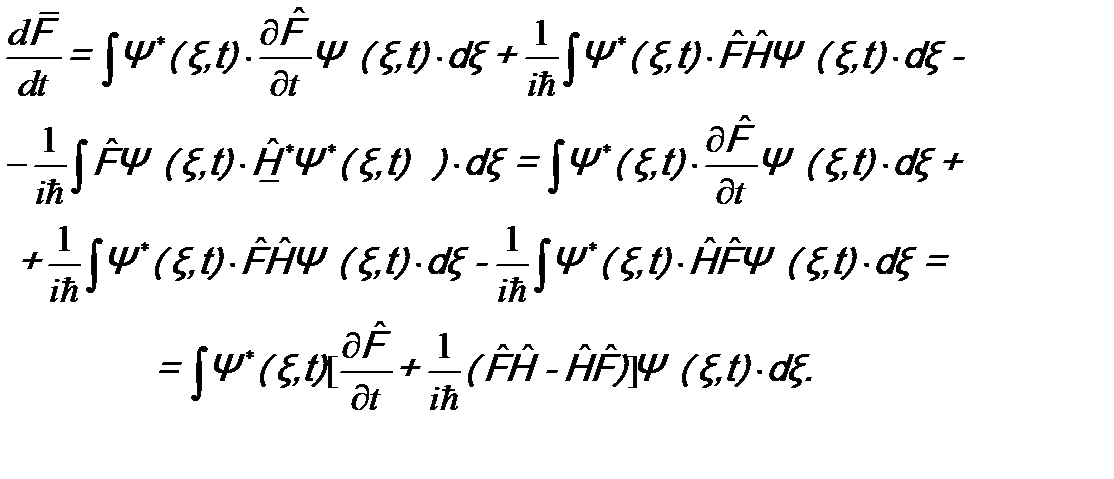
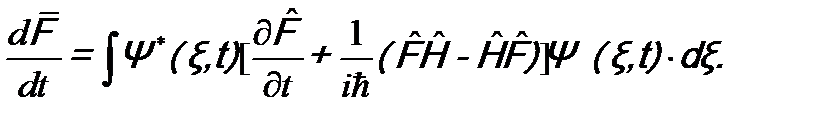 (13.2)
(13.2)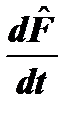 , который называется «производной оператора по времени»:
, который называется «производной оператора по времени»: . (13.3)
. (13.3) - коммутатор операторов
- коммутатор операторов 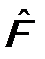 и
и 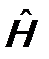 .
.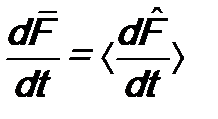 . (13.4)
. (13.4)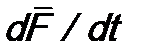 , используя определение (13.3) оператора
, используя определение (13.3) оператора 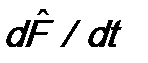 .
.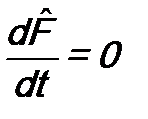 . Как видно из (13.3), для этого от оператора
. Как видно из (13.3), для этого от оператора 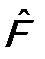 требуется выполнение двух условий:
требуется выполнение двух условий: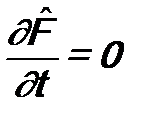 , т.е. оператор
, т.е. оператор 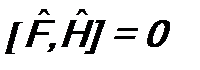 , т.е. оператор
, т.е. оператор 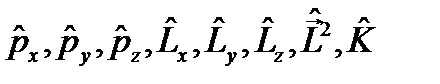 первое условие выполняется, поэтому необходимо вычислять их коммутаторы с гамильтонианом. Если для каких-то из них коммутаторы будут равны нулю, то эти физические величины и будут интегралами состояния микросистемы.
первое условие выполняется, поэтому необходимо вычислять их коммутаторы с гамильтонианом. Если для каких-то из них коммутаторы будут равны нулю, то эти физические величины и будут интегралами состояния микросистемы.


