
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постулат 1. О волновой функции
Волновая функция Ψ(ξ, t) полностью определяет состояние системы в данный момент времени t. Величина Постулат 2. О принципе суперпозиции Если система может находиться в состоянии, которому соответствует волновая функция Ψ1(ξ, t), или Ψ2(ξ, t),…, или Ψ n (ξ, t),…, то она может находиться и в состоянии, которому соответствует волновая функция
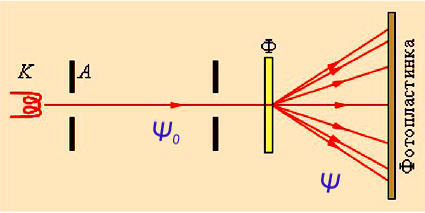
Сложное состояние с волновой функцией Ψ(ξ, t) называют суперпозицией «простых» состояний с волновыми функциями Ψ n (ξ, t) (n =1, 2, …). Дифракция электрона на кристалле. Волновая функция электрона до → До прохождения кристалла у электрона импульс был
Кот Шрёдингера: Измерение в квантовой механике разрушает суперпозицию и делает состояние микрочастицы определенным.
Постулат 3. О физических операторах квантовой механики Постулируется: Каждой динамической переменной классической механики в квантовой механике сопоставляется линейный эрмитовый оператор. Соотношение между операторами такое же, как и между динамическими переменными в классической механике. В классической механике для характеристики состояния системы используются динамические переменные:
Квантовая механика использует операторный формализм. Физические операторы имеют вид (вид некоторых из них впоследствии будет обоснован из свойств пространства-времени и законов сохранения): а). Оператор координаты Его действие на функцию сводится просто к умножению этой функции на соответствующую координату, т.е.
аналогично действие операторной функции
б). Оператор импульса
Соответственно векторный оператор импульса
Таким образом, в). Оператор момента импульса В классической механике оператор момента импульса имеет вид:
= = Отсюда следует, что компоненты векторного оператора
Наряду с операторами Операторы оператор Поскольку физически момент импульса связан с поворотами системы в пространстве, часто удобнее пользоваться его определением в сферической системе координат (r, θ, φ). В этой системе наиболее используемые на практике операторы
г). Оператор энергии Приведем сначала вид оператора кинетической энергии
Здесь m и
Δ – оператор Лапласа. Здесь использован вид операторов В классической механике полная энергия частицы равна:
Здесь
или Нередко требуется оператор Гамильтона не в декартовой, а в сферической системе координат. Он имеет вид:
Таблица физических операторов
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.009 с.) |
 определяет вероятность обнаружения N микрочастиц соответственно в точках
определяет вероятность обнаружения N микрочастиц соответственно в точках  в момент времени t.
в момент времени t. .
.
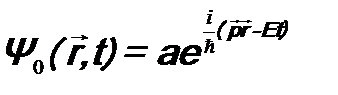 ; после →
; после → 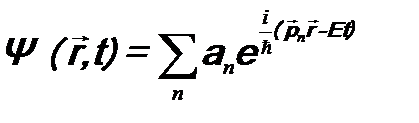 .
. , после прохождения кристалла он не имеет определенного значения.
, после прохождения кристалла он не имеет определенного значения.
 .
. - координата,
- координата,  - импульс,
- импульс, 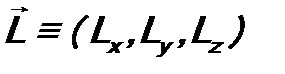 - момент импульса (иначе – момент количества движения), E - энергия.
- момент импульса (иначе – момент количества движения), E - энергия. .
.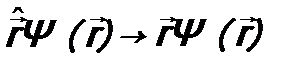 ;
; от
от 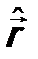 сводится просто к умножению на функцию
сводится просто к умножению на функцию 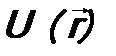 , т.е.
, т.е. .
.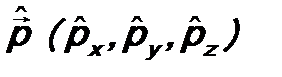 .
.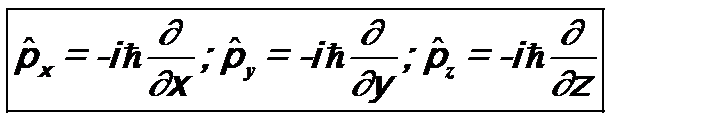 . (7.1)
. (7.1) имеет вид:
имеет вид: . (7.2)
. (7.2) выражается через известный в векторной алгебре оператор «набла»:
выражается через известный в векторной алгебре оператор «набла»: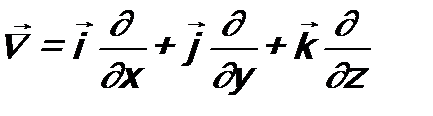 . (7.3)
. (7.3) .
. (
(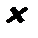 - знак векторного произведения). В соответствии с постулатом 3 оператор момента импульса будет иметь вид:
- знак векторного произведения). В соответствии с постулатом 3 оператор момента импульса будет иметь вид: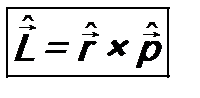 . (7.4)
. (7.4)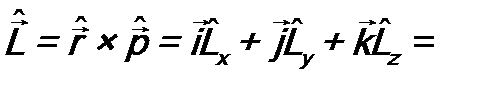
 =
=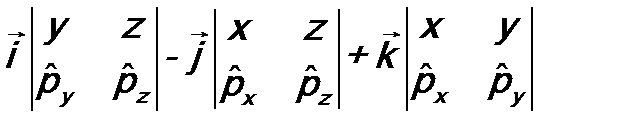 =
=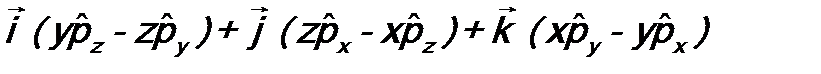 .
. 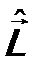 имеют вид:
имеют вид: . (7.5)
. (7.5) обычно рассматривают и оператор квадрата момента импульса
обычно рассматривают и оператор квадрата момента импульса  :
: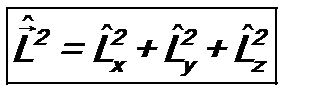 (7.6)
(7.6)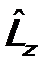 и
и 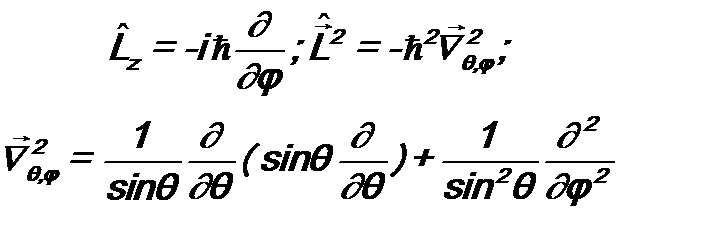 . (7.7)
. (7.7)  . В классической механике выражение для кинетической энергии имеет вид:
. В классической механике выражение для кинетической энергии имеет вид: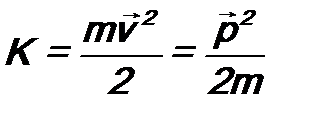 .
. - масса и скорость частицы,
- масса и скорость частицы, 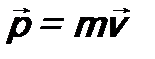 - ее импульс. В квантовой механике вводится лишь оператор импульса. Тогда в соответствии с постулатом 3 оператор кинетической энергии будет иметь вид:
- ее импульс. В квантовой механике вводится лишь оператор импульса. Тогда в соответствии с постулатом 3 оператор кинетической энергии будет иметь вид: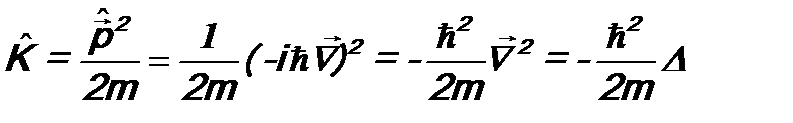 . (7.8)
. (7.8)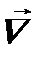 (см. ф-лы (7.2) и (7.3)) и учтено, что
(см. ф-лы (7.2) и (7.3)) и учтено, что . (7.9)
. (7.9) .
.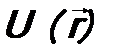 - потенциальная энергия частицы,
- потенциальная энергия частицы,  - функция Гамильтона. В соответствии постулатом 3 оператор полной энергии микрочастицы будет иметь вид:
- функция Гамильтона. В соответствии постулатом 3 оператор полной энергии микрочастицы будет иметь вид: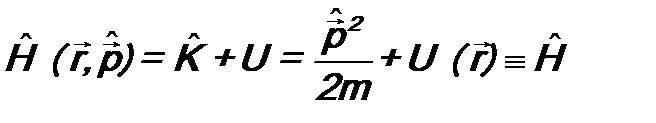 . (7.10)
. (7.10)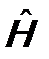 называется оператором Гамильтона. В явном виде
называется оператором Гамильтона. В явном виде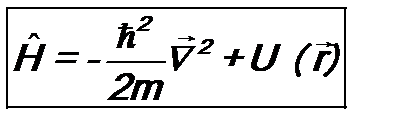 , (7.11)
, (7.11)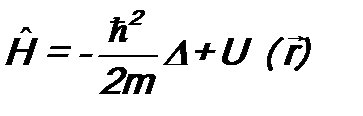 . (7.12)
. (7.12)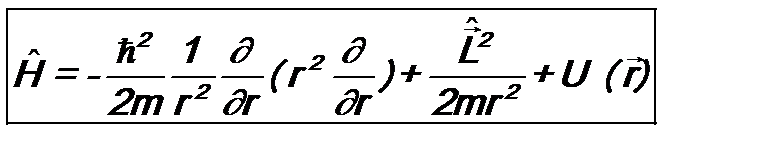 . (7.13)
. (7.13)


