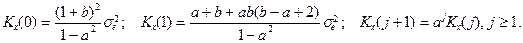Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрическое оценивание СПМСодержание книги
Поиск на нашем сайте Полученные операторные представления ряда x (k) обеспечивают, в частности, возможность проведения параметрического спектрального анализа:
Чтобы получить минимальное представление, содержащее наименьшее число параметров, желательно учесть в модели обе компоненты, так что
или, в операторной форме,
Такую модель называют моделью авторегрессии со скользящим средним:
Авторегрессия: процессы Маркова и Юла Временной ряд { x (k)} называется процессом Маркова, если он удовлетворяет модели авторегрессии первого порядка AR (1):
Очевидно,
поэтому при
если Временной ряд { x (k)} называется процессом Юла, если он удовлетворяет модели авторегрессии второго порядка AR (2):
или
Контрольные вопросы 1. Формирующий фильтр 2. Отбеливающий фильтр 3. Условия стационарности и обратимости 4. Параметрическое оценивание СПМ 5. Процесс Маркова и его свойства 6. Процесс Юла и его свойства Задания на лабораторную работу № 8 1. Сформировать выборку из стационарного процесса Юла 2. Интерпретировать ее как выходной сигнал системы, на вход которой подан гауссов белый шум. 3. Оценить СПМ процессов на входе и выходе в параметрической и в непараметрической форме 4. Проверить на данном примере выполнение основной теоремы теории линейных систем. ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛЕЙ Уравнения Юла-Уокера Уравнения, связывающие значения корреляционной функции процесса с коэффициентами ai, bj, называют уравнениями Юла-Уокера. Пример 9.1. Пусть временной ряд { x (k)} удовлетворяет модели авторегрессии второго порядка AR (2) - процесс Юла, уравнение (8.9). При моделировании такого ряда нужно обеспечить выполнение условий M x (1)=M x (2)=0, тогда, очевидно, M x (k)=0 для всех k. Требуется получить уравнения для ковариаций K (j)=M[ x (k) x (k – j) ], Возьмем основное уравнение (11)
домножим обе его части на x (k -1), x (k -2), x (k - j),
В формировании значений x (k -1), x (k -2),… участвуют случайные составляющие с номерами только до k -1, поэтому
В терминах ковариаций K (j) получаем систему уравнений
откуда
Обратно, если известны ковариации, то
Если известны оценки нескольких ковариаций, то оценки коэффициентов a 1, a 2 можно получить из системы (9.1) по МНК. Пример 9.2. Пусть временной ряд { x (k)} удовлетворяет модели ARMA (1,1):
Если обеспечить условие M x (1)=0, то, очевидно, M x (k)=0 для всех k. Требуется получить уравнения для ковариаций K (j)=M[ x (k) x (k – j) ], a) Возьмем основное уравнение (13), домножим обе его части на x (k -2) и перейдем в полученных соотношениях к математическим ожиданиям:
т.е. Kx (2)= aKx (1), Kx (j+1)= aKx (j), так что Kx (j +1)= a j Kx (1). Рассмотрим новый процесс
и вычислим его дисперсию и первую ковариацию двумя способами. b) Из первого выражения для y (k) в (9.3)
но, как показано в пункте a), Kx (2)= aKx (1), поэтому c) Из второго выражения для y (k) в (9.3)
Приравнивая выражения для моментов, полученные двумя разными способами, приходим к системе уравнений Юла-Уокера:
Таким образом, если имеются значения коэффициентов a, b,
В то же время, если известны значения, например, Kx (0), Kx (1), Kx (2), то уравнения для нахождения a, b,
|
||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

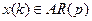 , т.е.
, т.е. 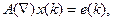 то его спектральная плотность мощности имеет вид
то его спектральная плотность мощности имеет вид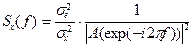 ;
;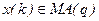 , т.е.
, т.е. 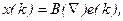 то его спектральная плотность мощности имеет вид
то его спектральная плотность мощности имеет вид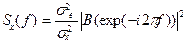 .
.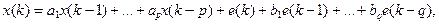
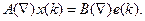
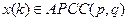 или
или 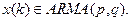 Спектральная плотность мощности такого процесса имеет вид
Спектральная плотность мощности такого процесса имеет вид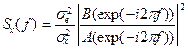 .
.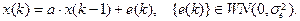

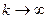 если
если 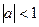 , то
, то 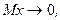
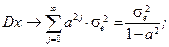
 , то ряды расходятся. Это значит, что смоделированный таким образом процесс
, то ряды расходятся. Это значит, что смоделированный таким образом процесс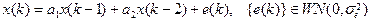 (8.8)
(8.8)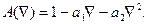 Условие устойчивости состоит в том, что оба корня
Условие устойчивости состоит в том, что оба корня 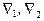 полинома
полинома 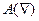 должны лежать внутри единичного круга комплексной плоскости. В терминах коэффициентов a 1, a 2 это означает, что они должны лежать внутри треугольника, приведенного на рис. 8.6. Спектральная плотность процесса (8.8) имеет вид
должны лежать внутри единичного круга комплексной плоскости. В терминах коэффициентов a 1, a 2 это означает, что они должны лежать внутри треугольника, приведенного на рис. 8.6. Спектральная плотность процесса (8.8) имеет вид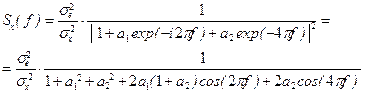
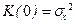 .
.
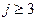 и перейдем в полученных соотношениях к математическим ожиданиям:
и перейдем в полученных соотношениях к математическим ожиданиям: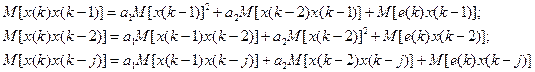
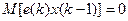 ,
, 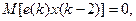
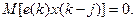

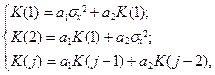 (9.1)
(9.1)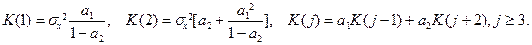
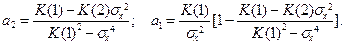
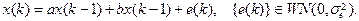 (9.2)
(9.2)
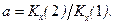 Аналогично получаем, что для всех j
Аналогично получаем, что для всех j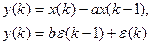 (9.3)
(9.3)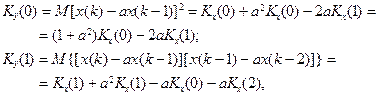

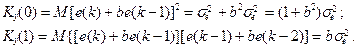
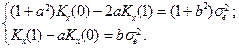
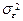 или их оценки, то
или их оценки, то