Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретизация. Частота Найквиста и теорема Котельникова
Исходный физический сигнал x (t) является непрерывной функцией времени и называется аналоговым. Числа xk = x (tk) называются отсчетами сигнала. Как правило, отсчеты берутся через равные промежутки времени Δ t – период или шаг дискретизации. Величина fd, обратная периоду дискретизации, называется частотой дискретизации:
Если Δ t выражен в секундах, то частота дискретизации выражается в герцах (Гц). При обработке сигнала в вычислительных устройствах его отсчеты округляются и представляются в виде двоичных чисел с конечным числом разрядов. Такое округление называется квантованием по уровню. Обычно дискретизация и квантование выполняются внутри одной микросхемы. Сигнал, дискретный по времени и квантованный по уровню, называется цифровым сигналом. Если в сигнале x (t) присутствует периодическая составляющая с периодом T <2Δ t, то есть с частотой f >1/2Δ t, то в дискретизованном сигнале она наблюдаться не будет, но в нем останутся ложные периодические составляющие с периодами 2 T, 3 T и т.д. Таким образом, частоту (аргумент f спектральной плотности) имеет смысл анализировать только на интервале [ -1/(2Δ t), 1/(2Δ t)]. Граничную частоту F = 1/(2Δ t) называют частотой Найквиста. Спектральную плотность в силу симметрии обычно рассматривают только на промежутке [0, 1/(2Δ t)], удваивая ее значения при положительных f для сохранения основных энергетических соотношений. Именно такая спектральная плотность измеряется на практике с помощью прямой фильтрации. Если для процесса x (t) заранее известно, что в нем отсутствуют периодические составляющие с частотами большими, чем некоторая величина F, то соответствующий дискретизованный процесс с шагом Δ t ≤1/(2 F) несет в себе всю информацию о частотном составе исходного x (t). Этот результат носит название теоремы Котельникова. Рассмотрим теперь ряд измерений { xk }, из которого тренд, сезонная составляющая и периодические составляющие либо исключены, либо их в нем не было. При этом, если речь идет о сравнении нескольких рядов, требуется, чтобы во всех них выделение этих составляющих было произведено одним и тем же способом. В большинстве случаев модель такого ряда { xk } можно построить, рассматривая его как результат дискретизации некоей реализации стационарного эргодического случайного процесса x (t):
xk = x (k D t). Еще одна важная возможность состоит в том, чтобы перейти в ряде { xk } к конечным разностям: yk = xk + 1 - xk; zk = yk + 1 - yk и т.д. Разности достаточно высокого порядка не содержат медленно меняющихся составляющих и их обычно можно изучать методами, применяемыми для стационарных рядов. Этот подход может использоваться в задачах распознавания, когда нужно создать некий обобщенный «портрет» ряда и сравнивать его с «портретами» других рядов, прошедших такую же обработку. Кроме того, многие процедуры прогнозирования исходного ряда можно получать из процедур прогнозирования рядов их конечных разностей. Ряд измерений { xk }, моделью которого является стационарный эргодический случайный процесс с дискретным временем, называется стационарным временным рядом. 7.2. Быстрое преобразование Фурье (БПФ) Для процесса с дискретным временем { xk }, xk = x (k Δ t), k =1,…, n сохраняются все введенные выше определения и результаты с той разницей, что интегралы заменяются суммами, а частоту (аргумент f спектральной плотности) имеет смысл рассматривать только на интервале [0 FN ], где FN = 1/(2Δ t) - частота Найквиста. В частности, прямое преобразование Фурье последовательности { xk } – непараметрическую оценку спектральной плотности F (f) - можно вычислить по формуле
обратное – по формуле
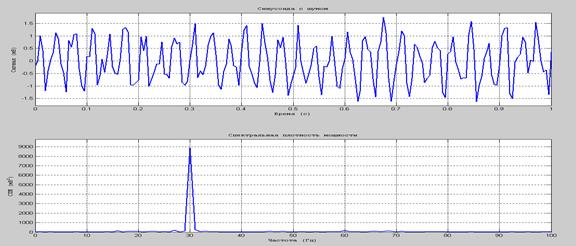
Вычисления по каждой из этих формул требуют n 2 операций. В 1966 г. Мак-Кован предложил геометрическую интерпретацию преобразования Фурье как некоторого поворота вектора x в n – мерном пространстве и показал, что его можно разложить на последовательность поворотов вокруг каждой из осей, что требует всего 4 n операций. Этот подход получил название быстрого преобразования Фурье, БПФ. Сейчас такие быстрые версии разработаны для всех основных интегральных преобразований. Благодаря технике БПФ при корреляционном анализе оказалось выгодным находить корреляционную функцию как обратное преобразование Фурье спектральной плотности, а не наоборот, как это делалось раньше. Пример вычисления БПФ в ИМС MatLab приведен в Документе 7.1 и проиллюстрирован на рис.7.1.
Все определения в области спектрального анализа построены так, чтобы формулы имели одинаковый вид как для детерминированных, так и для стационарных случайных рядов. Разница, как отмечалось выше, проявляется в основном в том, что для случайных процессов имеет смысл рассматривать только СПМ. При анализе сигнала s (t) на фоне аддитивного шума ξ(t) большое значение имеет безразмерный параметр snr (signal to noise ratio) – отношение сигнал/шум. В случае дискретного времени его определяют как отношение дисперсий:
Эту величину часто выражают в децибелах (дБ):
Для случайного ряда длиной n БПФ дает оценку СПМ S (f), значения которой представляют собой практически не коррелированные случайные величины с дисперсией порядка S 2(f), которая, очевидно, не убывает с ростом n. Основной выход состоит в том, чтобы вычислить оценки для набора интервалов, а затем усреднить. В ИМС MatLab широко используется функция spectrum, в которой реализован алгоритм Уэлча. В этой процедуре данный отрезок временного ряда разбивается на M (по умолчанию M =8) частично пересекающихся отрезков. В каждом отрезке удаляется линейный тренд, для каждого из остатков вычисляется БПФ с использованием одного из сглаживающих окон (по умолчанию используется окно Хеннинга) и результаты усредняются. Удаление линейного тренда приводит к небольшому смещению, поэтому результаты такого анализа могут несколько отличаться от результатов работы других спектроанализаторов.
Рис.7.1. СПМ синусоидального сигнала с частотой 30 Гц, наблюдаемого на фоне аддитивного шума. Отношение сигнал/шум snr = 2.8284=20.7944 дБ Контрольные вопросы 1. Частота дискретизации 2. Частота Найквиста 3. Теорема Котельникова 4. Быстрое преобразование Фурье (БПФ) 5. БПФ смеси синусоид 6. Отношение «сигнал-шум». Децибелы Задания на лабораторную работу № 7 1. Сформировать линейную систему с экспоненциально-убывающей весовой функцией 2. Сформировать выборку из стационарного процесса Юла и подать ее на вход системы 3. Получить процесс на выходе системы. 4. Оценить СПМ процессов на входе и выходе 5. Найти передаточную функцию системы 6. Проверить на примере выполнение основной теоремы теории линейных систем ПАРАМЕТРИЧЕСКИЙ АНАЛИЗ
|
||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.011 с.) |
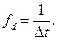
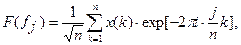
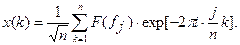
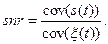
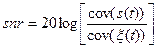 дБ.
дБ.