
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Социо-кибер-физические системыСтр 1 из 14Следующая ⇒
ВВЕДЕНИЕ
Электронное учебное пособие по дисциплине «Теория информационных процессов и систем» направлено на формирование универсальных компетенций в соответствии с федеральным государственным образовательным стандартом (ФГОС ВО 3++) по уровню бакалауреата: ПК-11 - Способность проектировать базовые и прикладные информационные технологии; ПК-14 - Способность использовать знание основных закономерностей функционирования биосферы и принципов рационального природопользования для решения задач профессиональной деятельности; ПК-22 - Способность проводить сбор, анализ научно-технической информации, отечественного и зарубежного опыта по тематике исследования. Электронное учебное пособие предназначено для обучающихся по направлению подготовки бакалауреата 09.03.02 «Информационные системы и технологии», и может быть использовано при изучении других дисциплин, направленных на формирование универсальных компетенций. В электронном учебном пособии содержится систематическое изложение основ современных методов информационного анализа процессов и систем, в том числе на основе моделей теории сигналов и математической статистики. Цель электронного учебного пособия – сформировать у обучающихся системные знания в области теории и практики анализа данных, развить коммуникативные компетенции, которые позволят и в будущем осуществлять профессиональную деятельность. Содержание данного электронного учебного пособия соответствует рабочей программе дисциплины и основано на материалах отечественных и зарубежных исследований в области анализа данных, включая современные публикации. Каждый раздел электронного учебного пособия включает контрольные вопросы и тестовые задания.
АННОТАЦИЯ ДИСЦИПЛИНЫ
Дисциплина «Теория информационных процессов и систем» относится к базовой части программы и изучается в 4-5 семестрах 2-го и 3-го курсов. Изучение дисциплины основано на принципах дальнейшего развития математических дисциплин базовой части программы, в том числе дисциплин «Математика», «Дополнительные главы математики», «Базовые информационные процессы и технологии», «Моделирование процессов и систем», а также дисциплины вариативной части «Проектирование информационных систем».
В качестве «входных» знаний, умений и готовностей требуется владение основными понятиями теории вероятностей, конечномерного линейного анализа, прежде всего операциями с матрицами и квадратичными формами. Освоение данной дисциплины как предшествующей необходимо для последующего овладения дисциплинами «Интеллектуальные информационные системы и технологии», «Инструментальные средства информационных систем», «Технологии обработки информации», «Технологии интеллектуального анализа данных» и для успешного выполнения ВКР. 2. Планируемые результаты обучения по дисциплине В результате освоения дисциплины обучающийся должен: Знать:
Уметь:
Владеть:
3. Объем дисциплины по видам учебных занятий Объем дисциплины составляет 5 зачетных единицы, всего 180 часов, из которых 48 часов составляет контактная работа обучающегося с преподавателем (36 часа занятий лекционного типа, 54 часов практических занятий), 90 часов составляет самостоятельная работа обучающегося). В конце 6-го семестра предусмотрен экзамен (36 часов)
ОГЛАВЛЕНИЕ
Системы и модели Система – это целостное образование, обладающее свойствами, не сводящимися к свойствам входящих в это образование элементов. Модель – это система, исследование которой служит средством для получения информации о другой системе (прототипе). Она должна обладать следующими свойствами:
Модель, отражающая с необходимой полнотой систему в содержательном аспекте и записанная на естественном языке с использованием положений наивной логики, называется концептуальной моделью. Различают дескриптивное концептуальное моделирование, в котором рассматриваются модели описательного характера, и прескриптивное (нормативное) концептуальное моделирование. Прескриптивные модели предписывают определенное поведение, определенные действия (прогнозирование, оптимизация). Аналитические модели Аналитическая математическая модель
Основной недостаток аналитического моделирования связан с тем, что для сложных систем необходима существенная идеализация как элементов, так и системы в целом. Имитационные модели Имитационная математическая модель
Основным достоинством имитационных моделей является возможность отражения таких свойств системы, как нелинейность, дискретность, вероятность срабатывания, разнородность элементов и разнообразие связей между ними, временная логика и др. Основным недостатком имитационной модели является недостаточность теоретической проработки и необходимость многократных экспериментов, состоящих в имитации процессов в системе при различных воздействиях. Однако даже при многократном экспериментировании фундаментальность выводов здесь уступает фундаментальности выводов, получаемых на аналитической модели (если ее возможно построить). Большие системы Одно из самых примечательных явлений, наблюдающихся сейчас в науке, - это стремление перейти от изучения хорошо организованных систем к плохо организованным или диффузным системам, к изучению задач с плохой структурой. Сейчас такие системы называют сложными. Иногда их называют также большими системами, поскольку здесь надо учитывать действие очень многих разнородных факторов, задающих различные по своей природе, но тесно взаимодействующие друг с другом процессы. Еще большие трудности возникают при попытке изучать такие диффузные системы, для которых неизвестны протекающие в них элементарные процессы. Примером служит, например, интеллект человека.
Модели вместо законов Переход от изучения хорошо организованных систем к изучению плохо организованных, сложных систем оказал влияние на общие концепции науки. Понятие закона в науке заменяется более широким, хотя и очень расплывчатым понятием модели. Сейчас наряду с учеными нового направления, занимающимися изучением плохо организованных систем, существуют ученые традиционного направления, занимающиеся изучением хорошо организованных систем. Много досадных недоразумений возникает, когда работы, выполненные с позиций статистических или кибернетических, обсуждаются учеными другого направления. Модель — это весьма многозначное понятие. В математику понятие модели было введено Клейном (70-е годы XIX века), а затем Расселом. Одно из применений этого понятия в математике состоит в доказательстве внутренней непротиворечивости теории путем нахождения реально существующей модели - то, что существует, не может быть внутренне противоречиво. П онятие математической модели, существующее сейчас в прикладной математике и кибернетике, можно противопоставить понятию закона в науке. Закон в науке имеет характер некоторой абсолютной категории на данном уровне знаний. Он может быть либо безусловно верен, либо безусловно неверен. Нельзя говорить о хороших и плохих законах или что одно и то же явление можно объяснить несколькими различными законами. Если в точных науках проявлялся дуализм (волна – частица), то он всегда вызывал чрезвычайную озабоченность, и в конце концов выяснялось, что какая-то одна сторона явления описывается одними закономерностями, другая - другими. Понятие модели отличается от понятия гипотезы. Наличие нескольких гипотез всегда рассматривали как некое временное явление. Если после выбора одной из конкурирующих гипотез удается представить ее в математической форме, то она приобретает статус закона. Математические же модели не всегда конкурируют друг с другом. Одни и те же аспекты изучаемой системы можно описывать различными моделями, одновременно имеющими право на существование. Для разных аспектов строятся разные модели. Многозначность понятий Раньше считалось, что язык математики строго однозначен и этим отличается от многозначного - полиморфного - естественного языка людей. Снижение требований, предъявляемых к математическому описанию, замена закона моделью привели к тому, что математический язык, однозначный по своей природе, стал применяться как многозначный. Начала стираться четкая грань, которая ранее существовала между математическим и словесным описанием явлений. Еще и сейчас очень часто можно слышать споры о возможности математического описания столь сложных систем, как, скажем, социальные системы. Те, кто утверждают, что нельзя, имеют в виду математическое описание в старом, традиционном смысле. Те же, кто говорит, что можно, исходят просто из совсем других концепций: под математическим описанием понимают не установление законов, а создание моделей. Человек и машина Одно из самых серьезных различий между человеком и компьютером состоит в том, что человек, в отличие от ЭВМ, может решать плохо сформулированные задачи. Иначе: машине нужен однозначный математический язык, человеку - естественный, полиморфный. Естественный язык, как раз в силу своей полиморфности, оказывается мощнее любого строго формализованного языка. Но пока еще никто не понял, как в сознании человека работает программа семантического анализа предложений, формулируемых на полиморфном языке. Эвристическое программирование — это перебор вариантов, но перебор с наложением некоторого ограничения. Вся эвристичность заключается именно в этом ограничении, налагаемом на перебор всех вариантов. Ограничения налагают, исходя только из интуитивных соображений, подражая деятельности человеческого интеллекта - строгого математического обоснования им не дается. Теорема Гёделя Обсудим в заключение модель системы, в которой возникают новые идеи - модель информационно развивающейся системы. Это самоорганизующиеся системы, которые управляются своими информационными потоками и при этом создают новую информацию. Такими являются биологическая система, создающая новые виды, наука, рассматриваемая как самоорганизующаяся система, интеллект человека, мыслящий автомат (если он возможен). Задачу можно поставить так: способна ли сколь угодно долго информационно развиваться система, состоящая из некоторой совокупности аксиом и правил обращения с ними? Аксиомы - это некоторые строки символов, а правила вывода - способы получения новых строк. Если правила конечны и строго детерминированы, то на такую систему накладывает ограничения известная теорема Гёделя о неполноте (1931). Из нее следует существование истин, выразимых на языке этой системы, которые, тем не менее, нельзя вывести из системы, как бы ни задавались аксиомы и конечные и детерминированные правила вывода. Генератор случая Из теоремы Гёделя следует, что информационно развивающуюся систему нужно освободить от детерминизма и она должна иметь какие-то степени свободы. В модель необходимо ввести что-то вроде генератора случайных чисел, случайным образом изменяющего систему аксиом и правила вывода. В биологической эволюции этот генератор реализуется, скажем, в виде жесткого излучения, действующего на гены. В модель нужно включить еще и блок обучения, отсеивающий неблагоприятные идеи. Должна существовать какая-то неизвестная нам система ограничений, налагаемых на генератор случая или на правила отбора генерированной идеи, а также ее проверки. Интересно, что пришелец с другой планеты не смог бы отличить систему, построенную таким образом, от системы, наделенной «свободной волей». Живое и неживое Генератор случая и блок обучения придают системе способность к адаптации. Система приобретает возможность нетривиально приспосабливаться к изменяющимся условиям. В биологии уже давно делались попытки провести границу между живой и неживой природой. Сейчас ясно, что это различие надо искать в особенностях организации информационной системы. В живой природе она построена так, что одной из основных ее особенностей является способность к адаптации. Так же организованы жизнеспособные системы, созданные человеком: наука и общество. В неживой природе, при росте кристалла или развитии плазмы, не происходит нетривиальных адаптационных процессов, т. е. система не обогащается информационно. В способности к адаптации больше, чем в чем-нибудь другом, проявляется грань между живой и неживой природой. Разложение Юла В 1927 году английский статистик Эдвин Юл предложил рассматривать временной ряд как аддитивную смесь четырех компонент: - тренда, или долгосрочного движения; - сезонной компоненты - колебаний относительно тренда с известным периодом, который можно определить на основе априорной информации; - периодической компоненты - колебаний, период которых определяется в ходе изучения данных; - остатка или несистематического случайного эффекта. Предположение аддитивности этих эффектов входит в исходную модель на правах гипотезы, которую, возможно, придется отвергнуть. Например, иногда имеющиеся данные могут потребовать модели с мультипликативным трендом – так устроены, в частности, сигналы с амплитудной модуляцией. Пространство сигналов Пусть на выходе некоторого измерительного устройства наблюдается сигнал x (t), представляющий собой зависимость напряжения от времени. Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся мощность равна
за время Т на резисторе выделится тепловая энергия
Если к этому резистору приложено переменное напряжение x (t), то за время [ Т 1, T 2] на нем выделится энергия
средняя мощность за это время
Полагая R =1, получаем определения энергии и средней мощности, принятые в теории сигналов. Если x (t) измеряется в вольтах (В), а время – в секундах (с), то мощность имеет размерность В2, а энергия - В2с. Если полная энергия x (t) конечна,
то такой сигнал называют интегрируемым с квадратом, или сигналом с ограниченной энергией. Многие важные соотношения теории сигналов требуют предположения о конечности энергии. Если это условие не выполняется (например, для периодических функций), приходится использовать специальные подходы, например, использовать аппарат обобщенных функций. Наиболее распространенная обобщенная функция – дельта-функция или функция Дирака δ(t). Ее можно представить как бесконечно узкий импульс с бесконечной амплитудой, сосредоточенный в точке t =0, при этом
Важнейшее свойство дельта-функции состоит в том, что для любой интегрируемой функции f (t), определенной в точке t 0, выполняется следующее соотношение:
4.2. Преобразование Фурье Прямым преобразованием Фурье сигнала x (t) называется функция
спектральная функция x (t), f – частота в герцах. Обратное преобразование имеет вид
Процесс x (t) дает представление сигнала в виде функции времени. Физический смысл F (f) состоит в том, что она дает представление того же сигнала в виде функции частоты. Для энергии сигнала выполняется равенство Релея
и его частный случай - равенство Парсеваля- Стеклова:
В этой связи величину
рассматривают как энергию сигнала в диапазоне частот [ f 1, f 2 ]. Если x (t) – вещественная функция, то значения спектральной функции на частотах f и – f являются комплексно-сопряженными: F (- f) = F *(f). Если x (t) – четная функция, то F (f) - вещественная четная. Если x (t) – нечетная функция, то F (f) – чисто мнимая нечетная. Модуль спектральной функции A (f) = | F (f) | называют амплитудным спектром, а аргумент φ(f) - фазовым спектром. Размерность амплитудного спектра та же, что у исходного сигнала (В), фазовый спектр – величина безразмерная. Для вещественного сигнала амплитудный спектр является четной, а фазовый – нечетной функцией частоты: | A (- f)|= | A (f) |; φ(- f)= - φ(f). Произведение длительности сигнала на ширину его спектра (база сигнала) не может быть меньше единицы (принцип неопределенности). Из этого следует, что можно сформировать сигнал большой длительности с широким спектром, но короткий сигнал с узким спектром существовать не может. Квадрат модуля спектральной функции сигнала S (f)=| F (f) |2 называют спектральной плотностью мощности или энергетическим спектром. Его размерность – В2. Корреляционная функция K (τ) сигнала x (t) с конечной энергией определяется как интеграл от произведения двух копий сигнала, сдвинутых на время τ:
Она показывает степень сходства между сигналом и его сдвинутой копией: чем она больше, тем сходство сильнее. Очевидно, что
и что при всех τ K (τ) ≤ K (0). Замечательный факт состоит в том, что корреляционная функция не зависит от фазового спектра сигнала и определяется только его энергетическим спектром по формулам:
Размерность K (τ) - В2с. К сожалению, этот подход годится только для сигналов с конечной энергией. Для периодических процессов с периодом T корреляционную функцию приходится вычислять, усредняя произведение сдвинутых копий в пределах одного периода
так что K (τ) является периодической функцией с периодом T, K (0) равно не энергии, а средней мощности, а ее размерность – не В2с, а В2. Задания на лабораторную работу № 5
ПАРАМЕТРИЧЕСКИЙ АНАЛИЗ Уравнения Юла-Уокера Уравнения, связывающие значения корреляционной функции процесса с коэффициентами ai, bj, называют уравнениями Юла-Уокера. Пример 9.1. Пусть временной ряд { x (k)} удовлетворяет модели авторегрессии второго порядка AR (2) - процесс Юла, уравнение (8.9). При моделировании такого ряда нужно обеспечить выполнение условий M x (1)=M x (2)=0, тогда, очевидно, M x (k)=0 для всех k. Требуется получить уравнения для ковариаций K (j)=M[ x (k) x (k – j) ], Возьмем основное уравнение (11)
домножим обе его части на x (k -1), x (k -2), x (k - j),
В формировании значений x (k -1), x (k -2),… участвуют случайные составляющие с номерами только до k -1, поэтому
В терминах ковариаций K (j) получаем систему уравнений
откуда
Обратно, если известны ковариации, то
Если известны оценки нескольких ковариаций, то оценки коэффициентов a 1, a 2 можно получить из системы (9.1) по МНК. Пример 9.2. Пусть временной ряд { x (k)} удовлетворяет модели ARMA (1,1):
Если обеспечить условие M x (1)=0, то, очевидно, M x (k)=0 для всех k. Требуется получить уравнения для ковариаций K (j)=M[ x (k) x (k – j) ], a) Возьмем основное уравнение (13), домножим обе его части на x (k -2) и перейдем в полученных соотношениях к математическим ожиданиям:
т.е. Kx (2)= aKx (1), Kx (j+1)= aKx (j), так что Kx (j +1)= a j Kx (1). Рассмотрим новый процесс
и вычислим его дисперсию и первую ковариацию двумя способами. b) Из первого выражения для y (k) в (9.3)
но, как показано в пункте a), Kx (2)= aKx (1), поэтому c) Из второго выражения для y (k) в (9.3)
Приравнивая выражения для моментов, полученные двумя разными способами, приходим к системе уравнений Юла-Уокера:
Таким образом, если имеются значения коэффициентов a, b,
В то же время, если известны значения, например, Kx (0), Kx (1), Kx (2), то уравнения для нахождения a, b, Оценивание порядка модели Определение для временного ряда { x (k)} адекватного порядка p, q модели ARMA (p, q) подчиняется тем же закономерностям, что и любой другой процесс моделирования. Для временных рядов обычно не удается разделить данные на обучающую и контрольную части, поэтому основной подход состоит в том, чтобы объяснить имеющуюся структуру данных с минимальным участием случайной составляющей. Таким образом, для различных выборов параметров порядка p, q предпочтение отдается тому варианту, который обеспечивает минимум оцененной дисперсии случайной составляющей:
Этот подход называют критерием ФОП – финальной ошибки прогнозирования. Минимизация ФОП может приводить к моделям достаточно высокого порядка, так что в критерий желательно ввести штраф за используемое число параметров. На этом пути японский математик Акаике сформулировал общий критерий ИКА - информационный критерий Акаике. Он получен на основе достаточно глубокого анализа энтропийных свойств метода максимального правдоподобия, однако для моделей ARMA (p, q) имеет крайне простой вид: ИКА = Контрольные вопросы 1. Прямые и обратные уравнения Юла-Уокера для моделей AR, MA, ARMA 2. Оценивание коэффициентов по МНК 3. Оценивание коэффициентов по уравнениям Юла-Уокера 4. Оценивание в замкнутом контуре 5. Критерии ФОП и Акаике Задания на лабораторную работу № 9 1. Сформировать выборку из стационарного процесса Юла 2. Интерпретировать ее как выходной сигнал системы, на вход которой подан гауссов белый шум. 3. Оценить параметры модели 3 различными способами 4. Оценить СПМ процессов на входе и выходе в параметрической и в непараметрической форме ПРОГНОЗИРОВАНИЕ Прогнозирование временного ряда всегда основывается на некоторой модели и должен опираться на понимание физики процесса. Если у ряда { x (k)} имеется физически объяснимый тренд, то первичный прогноз делается по нему. Полиномиальный тренд использовать опасно: он может явно присутствовать на конечном отрезке ряда, но не иметь отношения к экстраполяции за его пределы. Например, так может проявиться синусоида с большим периодом. В таких случаях рекомендуют перейти от исходного ряда к ряду его конечных разностей. Если у ряда { x (k)} на отрезке Горизонт прогноза Для различных моделей временных рядов с удаленным трендом можно определить так называемый горизонт прогноза. Белый шум имеет горизонт прогноза, равный нулю. Ряд, который можно описать как сумму нескольких синусоид на фоне аддитивного шума, имеет бесконечный горизонт прогноза. На этом этапе прогноз осуществляется по обнаруженной системе синусоид, его точность определяется дисперсией шумовой составляющей. Часть обнаруженных периодических составляющих может оказаться ложной: в любом случайном шуме могут идентифицироваться эфемерные периодичности. Для их устранения интервал наблюдения разбивается на части и выделяются только те синусоиды, которые устойчиво фиксируются во всех частях. Это – стандартная составляющая любых процедур спектрального анализа. Однако если в ряде присутствует синусоида с частотой f 0, то в его спектре, скорее всего, обнаружатся пики на кратных частотах 2 f 0, 4 f 0 и т.д. Классическим в экономике является пример 20-х годов XX века с исследованием динамики цен на пшеницу. В этом ряде было обнаружено 17 периодических составляющих, а на поверку оказалось, что его следует описывать как выход нелинейной системы, инициируемой одной-единственной периодической функцией. После того, как рассмотренные компоненты ряда идентифицированы и удалены, наступает этап анализа ряда остатков, который рассматривают как процесс с конечным горизонтом прогноза. К сожалению, структура остатков сильно зависит от методов, использованных на более ранних этапах. Например, для простейшей модели сигнала в виде синусоиды, наблюдаемой на фоне аддитивного белого шума, остаток будет представлять собой коррелированный ряд, причем его структура будет зависеть от того, каким методом оценивалась и удалялась эта синусоида. Во всех этих случаях исследователя подстерегает типичная ошибка, которая встречается даже в самых серьёзных работах. Дело в том, что для набора коэффициентов, наилучшим образом описывающего имеющиеся данные, могут оказаться нарушенными условия устойчивости, т
|
|||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.111.183 (0.114 с.) |
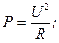
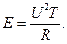
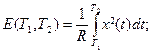
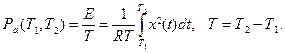
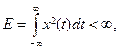
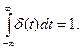
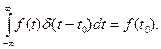
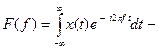
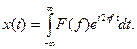 (4.1)
(4.1)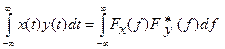
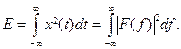
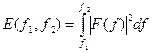
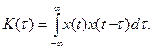
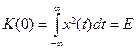
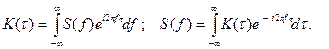
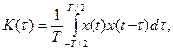
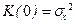 .
.
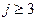 и перейдем в полученных соотношениях к математическим ожиданиям:
и перейдем в полученных соотношениях к математическим ожиданиям: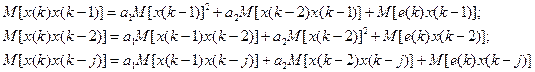
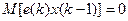 ,
, 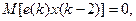
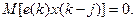

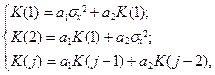 (9.1)
(9.1)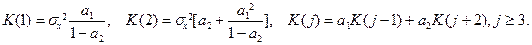
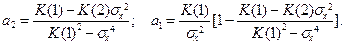
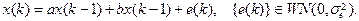 (9.2)
(9.2)
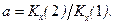 Аналогично получаем, что для всех j
Аналогично получаем, что для всех j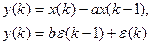 (9.3)
(9.3)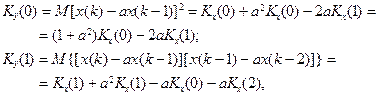

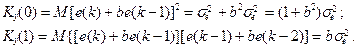
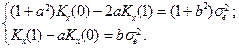
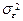 или их оценки, то
или их оценки, то
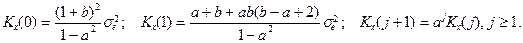
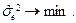
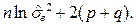 (9.6)
(9.6)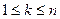 выявлен тренд в виде полинома порядка r, то его конечные разности порядка (r -1) будут содержать только линейный тренд, который уже может служить основой для прогноза.
выявлен тренд в виде полинома порядка r, то его конечные разности порядка (r -1) будут содержать только линейный тренд, который уже может служить основой для прогноза. 


