
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный анализ случайных процессов
5.1. Описание и классификация случайных процессов Опр. Случайный процесс ξ – это функция двух аргументов ξ = ξ(t,ω): Случайная величина ξ(t 0,ω) называется сечением процесса в момент t 0. Функция времени ξ(t 0,ω0) называется траекторией или выборочной функцией процесса. Случайный процесс задается семейством своих конечномерных распределений
где t 1,…, tk Конечномерные распределения должны обладать следующими свойствами:
2. 3. Если X – область значений процесса, то
Опр. Случайный процесс называется нормальным или гауссовым, если все его конечномерные распределения являются нормальными. Математическое ожидание и корреляционная функция Опр. Математическое ожидание: Корреляционная функция:
Дисперсия: Для комплексных процессов
Опр. Случайный процесс называется нормальным или гауссовым, если все его конечномерные распределения являются нормальными. Теорема. Гауссов процесс полностью определяется своими математическим ожиданием и корреляционной функцией. Действительно, пусть процесс ξ(t) – гауссов, для него заданы его a (t) и K (s, t). Рассмотрим последовательность моментов времени t 1< t 2<…< tn и соответствующий случайный вектор
Для двух процессов
Свойства корреляционной функции 1. 2. Для любых t 1,…, tn из T и любых z 1,…, zn из С
Такие функции называются неотрицательно определенными ядрами. Действительно, 3. Теорема. Если a (t) – произвольная, а K (s, t) удовлетворяет на M ξ(t) = a (t), K ξ(s, t) = K (s, t). 4. Это следует из очевидного неравенства a 2+ b 2
5. Это следует из неравенства Коши-Буняковского 6. Если K (s, t) непрерывна на диагонали, т.е. K (s, s) непрерывна, то она непрерывна во всех точках Действительно,
Аналогично доказывается, что если K (s, t) дифференцируема на диагонали, т.е. K (s, s) дифференцируема, то она дифференцируема во всех точках 7. K ξη(s, t) непрерывна тогда и только тогда, когда непрерывна K ξη(s, s); 8. K ξη(s, t) дифференцируема тогда и только тогда, когда дифференцируема K ξη(s, s).
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.7.85 (0.009 с.) |
 . В качестве аргумента t чаще всего выступает время, тогда T = [0,
. В качестве аргумента t чаще всего выступает время, тогда T = [0, 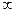 ). Процессы с многомерным Т называются случайными полями. Часто приходится рассматривать комплексные процессы ξ(t,ω):
). Процессы с многомерным Т называются случайными полями. Часто приходится рассматривать комплексные процессы ξ(t,ω): 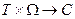 и векторные процессы ξ(t,ω):
и векторные процессы ξ(t,ω): 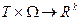 .
. 
 , A 1,…, Ak - борелевские множества из области значений процесса.
, A 1,…, Ak - борелевские множества из области значений процесса.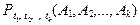 является совместным распределением k –мерного случайного вектора.
является совместным распределением k –мерного случайного вектора. для любой перестановки i 1,…, ik.
для любой перестановки i 1,…, ik.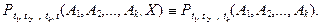
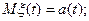

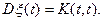
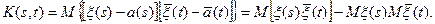
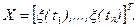 Он заведомо является гауссовым,
Он заведомо является гауссовым,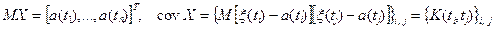 :
:
 рассматривается еще их взаимная корреляционная функция
рассматривается еще их взаимная корреляционная функция
 для комплексных процессов
для комплексных процессов 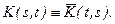


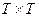 условиям 1,2, то существует гауссов случайный процесс ξ(t), для которого
условиям 1,2, то существует гауссов случайный процесс ξ(t), для которого .
. 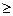 2 ab.
2 ab.
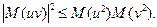


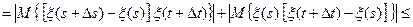
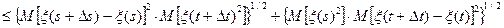 .
.


