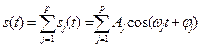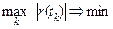Построение динамических моделей по экспериментальным данным

Временным рядом называют семейство измерений, упорядоченное по некоторому параметру, в качестве которого, как правило, выступает вре­мя. Обычно рассматривают либо ряды { x (t)}, t Î [0, T ] с непрерывным временем, либо ряды { x_k }, x_k = x (t_k), k = 1 ,..., n с дискретным временем и измерениями, сделанными через равные интервалы времени, t_k = k D t. Наиболее простые задачи можно ставить также и для рядов, заданных на достаточно частой неравномерной сетке. Для более сложного анализа такие ряды обычно интерполируют и используют их оценки их значений на равномерной сетке, но это – достаточно сложная операция, требующая в каждом случае особого рассмотрения. 

     Основная задача состоит в построении математической модели, объ­ясняющей механизм формирования ряда. В качестве объекта исследования может выступать как изолированный ряд, так и ансамбль рядов, получен­ных в одних и тех же условиях. Кроме того, часто рассматриваются задачи о связи между рядами, например, о механизме, с помощью которого один ряд (выходной сигнал) получается из другого (входного сигнала).

  Задача интерполяции. Предполагается, что значения x _k не содержат погрешностей и за ними стоит некоторая зависимость x (t), которую требуется восстановить. В этом случае можно:

• Провести через все точки { x (t_k)} полином P (t) степени (n -1). Коэффициенты полинома определятся из системы линейных уравнений P (t_k) = x (t_k).
• Провести через все точки { x (t_k)} кубический сплайн S (t). При этом в промежутках между точками t_k S (t) представляет собой полином 3-ей степени, а в самих точках t_k соседние полиномы склеиваются между собой так, чтобы обеспечить непрерывность второй производной S (t). Существуют сплайны гораздо более сложной структуры, чем кубические.

      В ИМС MatLab эти задачи решают процедуры-функции interp и spline (справка: help interp и help spline). Там же можно найти процедуры многомерной интерполяции.

      Гораздо более сложной является задача экстраполяции или прогнозирования данных x (t_k) за пределы промежутка [ t ₁ t_n ]. Она не имеет простого общего решения и требует детального учета всей дополнительной информации о процессе, порождающем измерения x (t_k).

     Задача сглаживания (непараметрическое оценивание тренда). В наиболее распространенных случаях при анализе временного ряда { x _k = x (t_k), k = 1,…, n } сначала в нем пытаются выделить низкочастотную составляющую – тренд a (t) и остаток r (t):

x (t) = a (t) + r (t).

Из остатка пытаются выделить сезонные составляющие

 
– периодические части с известными и физически понятными периодами ω _j:

r (t) = s (t)+ξ(t).

Остаток изучают специальными методами статистики случайных процессов. Имеются сложные процедуры, позволяющие в некоторых случаях провести весь анализ в одном блоке.

   В большинстве случаев при оценивании тренда используется метод наименьших квадратов (МНК). Если в ряде могут оказаться выпадающие измерения, используется метод наименьших модулей (МНМ) и другие альтернативы МНК. Иногда возникают специальные задачи, когда, например, требуется так выделить тренд, чтобы

(задача чебышевской аппроксимации).

   Для многомерного ряда { X _k = X (t_k), k = 1,…, n } тренд выделяют для каждой компоненты в отдельности. По поводу остатка обычно принимают гипотезу стационарной связанности – тогда можно перейти в остатке к главным компонентам, изучить их по отдельности, а затем с помощью обратного преобразования вернуться к исходным величинам. Именно из-за отсутствия стационарной связанности формальные математические методы плохо работают, например, на бирже.

   Во многих задачах на роль тренда удается подобрать подходящее семейство кривых и задача сводится к оцениванию нескольких заранее неизвестных параметров. Это – задача параметрического сглаживания, основанная на процедурах нелинейной регрессии. В версиях ИМС MatLab, начиная с 7.0, этим целям служит библиотека CurveFit (справка: help curvefit). 

Разложение Юла

В 1927 году английский статистик Эдвин Юл предложил рассматривать временной ряд как аддитивную смесь четырех компонент:

- тренда, или долгосрочного движения;

- сезонной компоненты - колебаний относительно тренда с известным периодом, который можно определить на основе априорной информации;

- периодической компоненты - колебаний, период которых определя­ется в ходе изучения данных;

- остатка или несистематического случайного эффекта.

Предположение аддитивности этих эффектов входит в исходную модель на правах гипотезы, которую, возможно, придется отвергнуть. Например, иногда имеющиеся данные могут потребовать модели с мультипликативным трендом – так устроены, в частности, сигналы с амплитудной модуляцией.