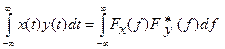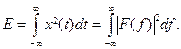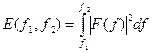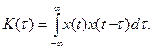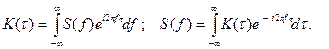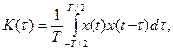Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный и спектральный анализ детерминированных процессов
Пространство сигналов Пусть на выходе некоторого измерительного устройства наблюдается сигнал x (t), представляющий собой зависимость напряжения от времени. Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся мощность равна
за время Т на резисторе выделится тепловая энергия
Если к этому резистору приложено переменное напряжение x (t), то за время [ Т 1, T 2] на нем выделится энергия
средняя мощность за это время
Полагая R =1, получаем определения энергии и средней мощности, принятые в теории сигналов. Если x (t) измеряется в вольтах (В), а время – в секундах (с), то мощность имеет размерность В2, а энергия - В2с. Если полная энергия x (t) конечна,
то такой сигнал называют интегрируемым с квадратом, или сигналом с ограниченной энергией. Многие важные соотношения теории сигналов требуют предположения о конечности энергии. Если это условие не выполняется (например, для периодических функций), приходится использовать специальные подходы, например, использовать аппарат обобщенных функций. Наиболее распространенная обобщенная функция – дельта-функция или функция Дирака δ(t). Ее можно представить как бесконечно узкий импульс с бесконечной амплитудой, сосредоточенный в точке t =0, при этом
Важнейшее свойство дельта-функции состоит в том, что для любой интегрируемой функции f (t), определенной в точке t 0, выполняется следующее соотношение:
4.2. Преобразование Фурье Прямым преобразованием Фурье сигнала x (t) называется функция
спектральная функция x (t), f – частота в герцах. Обратное преобразование имеет вид
Процесс x (t) дает представление сигнала в виде функции времени. Физический смысл F (f) состоит в том, что она дает представление того же сигнала в виде функции частоты. Для энергии сигнала выполняется равенство Релея
и его частный случай - равенство Парсеваля- Стеклова:
В этой связи величину
рассматривают как энергию сигнала в диапазоне частот [ f 1, f 2 ]. Если x (t) – вещественная функция, то значения спектральной функции на частотах f и – f являются комплексно-сопряженными: F (- f) = F *(f). Если x (t) – четная функция, то F (f) - вещественная четная. Если x (t) – нечетная функция, то F (f) – чисто мнимая нечетная.
Модуль спектральной функции A (f) = | F (f) | называют амплитудным спектром, а аргумент φ(f) - фазовым спектром. Размерность амплитудного спектра та же, что у исходного сигнала (В), фазовый спектр – величина безразмерная. Для вещественного сигнала амплитудный спектр является четной, а фазовый – нечетной функцией частоты: | A (- f)|= | A (f) |; φ(- f)= - φ(f). Произведение длительности сигнала на ширину его спектра (база сигнала) не может быть меньше единицы (принцип неопределенности). Из этого следует, что можно сформировать сигнал большой длительности с широким спектром, но короткий сигнал с узким спектром существовать не может. Квадрат модуля спектральной функции сигнала S (f)=| F (f) |2 называют спектральной плотностью мощности или энергетическим спектром. Его размерность – В2. Корреляционная функция K (τ) сигнала x (t) с конечной энергией определяется как интеграл от произведения двух копий сигнала, сдвинутых на время τ:
Она показывает степень сходства между сигналом и его сдвинутой копией: чем она больше, тем сходство сильнее. Очевидно, что
и что при всех τ K (τ) ≤ K (0). Замечательный факт состоит в том, что корреляционная функция не зависит от фазового спектра сигнала и определяется только его энергетическим спектром по формулам:
Размерность K (τ) - В2с. К сожалению, этот подход годится только для сигналов с конечной энергией. Для периодических процессов с периодом T корреляционную функцию приходится вычислять, усредняя произведение сдвинутых копий в пределах одного периода
так что K (τ) является периодической функцией с периодом T, K (0) равно не энергии, а средней мощности, а ее размерность – не В2с, а В2.
|
|||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.35.77 (0.006 с.) |
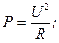
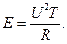
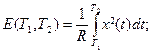
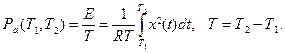
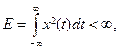
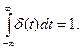
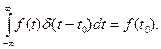
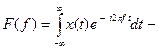
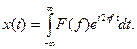 (4.1)
(4.1)