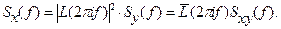Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стационарные процессы в линейных системах
Линейная система – это оператор A, на вход которого подается процесс x (t), а на выходе получается процесс y (t)= A x (t), при этом для любой линейной комбинации α x 1(t)+β x 2(t) A [ α x 1(t) + β x 2(t) ]= α A x 1(t) + β A x 2(t). Операторы с такими свойствами хорошо известны, в частности, это производная и интеграл. Оказывается, что любая линейная система имеет представление в виде интеграла
В подавляющем большинстве практически важных случаев можно считать, что свойства выходного сигнала в момент t зависят только от прошлых значений входного сигнала x (s), поэтому
Функцию w (t, s) называют весовой функцией линейной системы. Если w (t, s) зависит только от разности t - s, w (t, s)= w (t - s,0), система называется однородной. Физически это означает, что свойства системы постоянны в любой момент времени. Весовую функцию такой системы обозначают w (τ):
так что выход такой системы – это просто свертка входного сигнала и весовой функции, а универсальный аппарат для работы со свертками – это преобразование Лапласа L. Если x (s)=δ(s), т.е. на вход системы подается короткий импульс, моделируемый как дельта-функция, то, согласно (6.2),
Это значит, что весовую функцию линейной системы можно оценить экспериментально, подавая на вход системы короткие импульсы в различные моменты s. Если входной сигнал имеет постоянную составляющую a =M x (t), то его нужно рассматривать как сумму этой составляющей и центрированного сигнала с нулевым математическим ожиданием. Постоянная составляющая преобразуется по основной формуле (3). Дальнейшие рассмотрения касаются центрированного сигнала x (t) с нулевым математическим ожиданием. Преобразование Лапласа весовой функции
называют передаточной функцией системы. В большинстве случаев весовая функция быстро убывает с ростом τ, поэтому сходимость интеграла в (6.4) обеспечена и передаточную функцию можно рассматривать для чисто мнимых значений ее аргумента. Такую функцию φ(iu) называют амплитудно-фазовой частотной характеристикой или, короче, спектральной характеристикой системы.
Основная теорема теории линейных систем. Спектральные плотности входного Sx (u) и выходного Sy (u) сигналов связаны соотношением
Доказательство. Вычислим двумя способами автокорреляционную функцию Ky (s, t) выходного сигнала y (t). Можно заранее предположить, что она зависит только от разности s - t. С одной стороны, С другой стороны,
Подставим вместо x (s 1) и x (s 2) их представления по формуле (6.1) и изменим порядок интегрирования:
Введем в двух первых интегралах вместо s 1 и t 1 новые переменные s 2 и t 2 по формулам s 2= s - s 1, t 2= t - t 1. Тогда разность под знаком экспоненты приобретет следующий вид: s 1 - t 1 = s - s 2 – t + t 2 = (s - t) – (s 2 - t 2). Окончательно имеем:
Сравнивая две формулы для автокорреляционной функции (4) и (5), видим, что, действительно,
Взаимная спектральная плотность входа и выхода Sxy (u) определяется как обратное преобразование Фурье от взаимной корреляционной функции
В отличие от обычной спектральной плотности она обычно не является вещественной и положительной. Теорема. Доказательство этой формулы полностью аналогично приведенному выше доказательству основной теоремы. Пример 6.1. Оператор дифференцирования. Пусть x (t) – стационарный случайный процесс с нулевым математическим ожиданием. Для обеспечения сходимости интегралов потребуем, чтобы его спектральная плотность Sx (u) удовлетворяла условию
Рассмотрим линейное преобразование со спектральной характеристикой φ(iu) = iu. Запишем эту характеристику в виде
Тогда на выходе линейной системы получается процесс
В частности, это означает, что при ограничениях, обеспечивающих сходимость интегралов, спектральное представление (1) можно дифференцировать по t под знаком интеграла:
Пример 6.2. Решение линейного стохастического дифференциального уравнения. Пусть линейная система задана в виде дифференциального уравнения
Ay = так что d Ф x (u)= A (iu) d Ф y (u). Тогда, повторяя рассуждения, проведенные выше при доказательстве основной теоремы теории линейных систем, получаем связь между спектральными плотностями:
На практике линейные системы часто предпочитают описывать линейными дифференциальными уравнениями вида Ly (t) = x (t),
Пусть
Прямое численное решение линейных стохастических дифференциальных уравнений может приводить к несколько различным временным рядам в зависимости от метода интегрирования. Обычно удовлетворительные результаты дает модифицированный метод Эйлера (для стохастических уравнений его называют методом Хьюна) или методы Рунге-Кутты, однако нужно иметь в виду, что точность метода, рассчитанная для детерминированных уравнений, в стохастическом случае снижается на порядок. При этом существуют две "ловушки", в которые часто попадают начинающие исследователи: 1. Для стохастических уравнений чрезвычайно трудно построить корректную разностную схему, определяющую аппроксимации производных высших порядков, поэтому уравнения высших порядков всегда следует сводить к системе уравнений первого порядка. 2. Нелинейные уравнения всегда сводятся к соответствующему интегральному уравнению, при этом должно быть точно определено, какая конструкция стохастического интеграла имеется в виду.
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.129.100 (0.008 с.) |
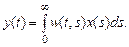

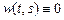 при s > t, так что интеграл берется в пределах от 0 до t:
при s > t, так что интеграл берется в пределах от 0 до t: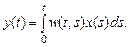
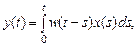 (6.3)
(6.3)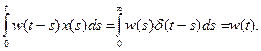
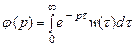 (6.4)
(6.4)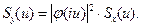
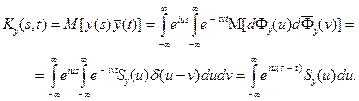 (6.5)
(6.5)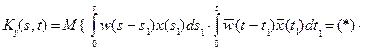
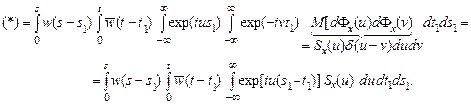
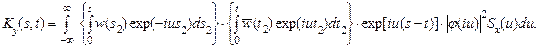 (6.6)
(6.6)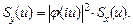
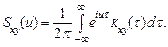
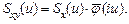
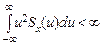 .
.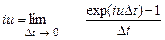 .
.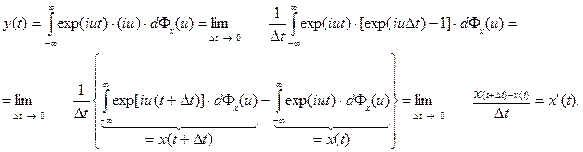
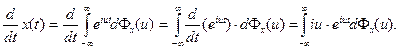 (6.7)
(6.7)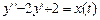 , или, в более общем виде, A y = x (t), где A
, или, в более общем виде, A y = x (t), где A 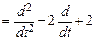 - линейный дифференциальный оператор. Ему ставится в соответствие характеристический полином A (iu) = (iu)2 - 2(iu) + 2. Входным сигналом является стационарный случайный процесс x (t) с нулевым средним и спектральной плотностью Sx (u). Тогда, согласно результатам примера 6.1,
- линейный дифференциальный оператор. Ему ставится в соответствие характеристический полином A (iu) = (iu)2 - 2(iu) + 2. Входным сигналом является стационарный случайный процесс x (t) с нулевым средним и спектральной плотностью Sx (u). Тогда, согласно результатам примера 6.1,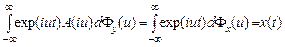 ,
,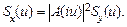
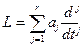 .
.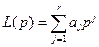 - характеристический многочлен дифференциального оператора L, тогда передаточная функция имеет вид φ(p) = [ L (p) ]-1, так что
- характеристический многочлен дифференциального оператора L, тогда передаточная функция имеет вид φ(p) = [ L (p) ]-1, так что