Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
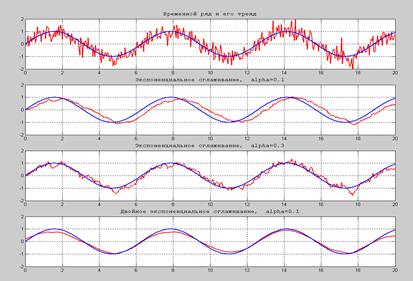
Экспоненциальное сглаживание
При экспоненциальном сглаживании вводится начальное значение сглаживающей функции
Если взять переменное a, a = 1/(k + 1), получится вычисление среднего в рекуррентной форме. При a=1 Очевидно, что при непараметрическом сглаживании нет четкой границы между трендом и низкочастотными колебаниями относительно тренда. Фактически эти процедуры представляют собой различные конструкции низкочастотных фильтров.
Любая процедура выделения тренда всегда искажает корреляционную структуру случайных погрешностей. В частности, в остатках от сглаживания появляется некая ложная периодическая составляющая, что является причиной многочисленных ошибочных «открытий». Этот эффект называется эффектом Слуцкого-Юла.
Рис.2.2. Экспоненциальное сглаживание Контрольные вопросы 1. Временной ряд 2. Цели моделирования 3. Задачи интерполяции и экстраполяции 4. Разложение Юла 5. Локально-полиномиальное сглаживание 6. Экспоненциальное сглаживание Задания на лабораторную работу №2 Смоделировать временной ряд (1000 измерений), содержащий медленно меняющуюся периодическую компоненту (тренд) и более быстро меняющуюся сезонную компоненту (с известной частотой). 1. Получить 2 непараметрические оценки тренда 2. Выделить ряды остатков и оценить в них амплитуду и фазу сезонной составляющей 3. Вывести графики всех изученных рядов 4. Сформулировать выводы о влиянии метода выделения тренда на точность оценивания параметров сезонной составляющей. 3. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ
|
|||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.107.241 (0.003 с.) |
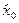 , задается параметр a Î [0,1] - коэффициент дисконтирования (обесценивания), а затем каждое следующее значение определяется по рекуррентной формуле
, задается параметр a Î [0,1] - коэффициент дисконтирования (обесценивания), а затем каждое следующее значение определяется по рекуррентной формуле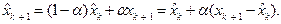
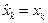 - сглаживания не происходит. При a<1 степень сглаживания увеличивается с уменьшением a, но при этом в оценке появляется смещение. Для устранения смещения сглаживание, если возможно, проводят дважды: слева направо, а затем в обратном порядке, справа налево. Эти процедуры проиллюстрированы на рис.4, соответствующий сценарий приведен в Документе 2. Можно рассматривать аналогичные процедуры с большим числом параметров (фильтры Брауна) и с адаптивной настройкой параметра a (фильтры Хольта).
- сглаживания не происходит. При a<1 степень сглаживания увеличивается с уменьшением a, но при этом в оценке появляется смещение. Для устранения смещения сглаживание, если возможно, проводят дважды: слева направо, а затем в обратном порядке, справа налево. Эти процедуры проиллюстрированы на рис.4, соответствующий сценарий приведен в Документе 2. Можно рассматривать аналогичные процедуры с большим числом параметров (фильтры Брауна) и с адаптивной настройкой параметра a (фильтры Хольта).