
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И классификация. Анализ источников погрешностей измерений, методы и средства их исключения и уменьшенияСодержание книги
Поиск на нашем сайте
Измерением называется нахождение значения физической величины опытным путем с помощью специальных технических средств. При проведении технических измерений имеют место многократные измерения (наблюдения) и однократные измерения. Однократное измерение – измерение, выполненное один раз. Многократное измерение – измерение одной и той же физической величины, результат которого получен из нескольких следующих друг за другом измерений (наблюдений), т.е. измерение, состоящее из ряда однократных измерений. Любые измерения направлены на получение результата, т.е. оценки истинного значения физической величины в принятых единицах. Вследствие несовершенства средств и методов измерений, воздействия внешних факторов и многих других причин результат каждого измерения неизбежно отягощен погрешностью. При этом точность измерения тем выше, чем ближе результат измерения оказывается к истинному значению. Количественной характеристикой качества измерений является погрешность измерения, определяемая как разность между измеренным где Строго говоря, применение формулы (5) для вычисления погрешности измерения невозможно. Поскольку истинное значение измеряемой величины неизвестно. Поэтому это выражение погрешности используется только в теоретических исследованиях, а на практике Поскольку действительное значение измеряемой величины только с той или иной степенью приближения заменяет истинное, то погрешность измерения, найденная относительно действительного значения, будет отличаться от погрешности измерения, которая могла бы быть найдена относительно истинного значения и является приближенной оценкой «истинной» погрешности измерения. Погрешность, выраженная в соответствии с формулами (5) и (6) имеет размерность измеряемой величины и называется абсолютной погрешностью, т.е. это разность между значением величины, полученным при измерении и ее истинным значением. Относительная погрешность измерения – это отношение абсолютной погрешности к истинному значению измеряемой величины. Как уже говорилось, погрешность измерения возникает в результате наложения элементарных погрешностей, вызываемых разными причинами. В зависимости от причины возникновения различают следующие виды погрешностей. Инструментальная погрешность – составляющая погрешности измерения, зависящая от погрешностей применяемых средств (качества их изготовления). Погрешность метода измерения – составляющая погрешности измерения, вызванная несовершенством метода измерения. Погрешность настройки - составляющая погрешности измерения, возникающая из-за несовершенства осуществления процесса настройки. Погрешность отсчитывания - составляющая погрешности измерения, вызванная недостаточно точным отсчитыванием показаний средств измерений (например, погрешность параллакса). Погрешность поверки – погрешность измерений при поверке средств измерений. Рассмотренные выше причины вызывают появление систематических и случайных погрешностей, из которых складывается суммарная погрешность измерения. Эти причины могут приводить к грубым погрешностям измерений. Систематическая погрешность является составляющей погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. К систематическим относятся, например, погрешности от неисправности прибора или от несоответствия действительного значения меры ее номинальному значению. Систематические погрешности могут быть изучены опытным путем и исключены из результатов измерений. В целях исключения систематической погрешности вводится поправка – значение величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению величины с целью исключения систематической погрешности. Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины, вследствие большого числа неподдающихся учету причин. Например, погрешности от вариации показаний измерительного прибора, погрешности округления или отсчитывания показаний прибора. Случайные погрешности нельзя исключить из результатов измерений, но их влияние можно уменьшить путем многократных повторных наблюдений одной величины и обработкой опытных данных. Грубая погрешность – погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность. Результаты измерений, содержание грубые погрешности, исключаются как недостоверные. Графическая интерпретация составляющих погрешности результата измерения приведена на рис. 58.
Рис.58. Составляющие погрешности измерения
Для оценки возможной погрешности измерений необходимо знать закономерности появления случайных погрешностей. При большом числе наблюдений их значения, как правило, распределяются по закону Гаусса. Распределение значений случайных погрешностей
где Вероятность появления погрешности
Для графического определения вычерчивается кривая Случайную погрешность можно уменьшить путем многократных наблюдений. Если какую-либо величину измерять много раз, то вероятным значением этой величины, или ее математическим ожиданием, будет среднее арифметическое значение
Погрешность результата измерения и среднее квадратическое отклонение результата измерения вычисляют по формулам
Погрешность результата измерения (среднего арифметического значения) уменьшается при увеличении числа наблюдений. Если при обработке результатов наблюдений выявлены грубые погрешности При измерениях случайные и систематические погрешности проявляются одновременно. Если систематические погрешности отсутствуют или учтены поправками, то суммарная предельная погрешность измерения
где Выбор средств измерений
Выбор средства измерения определяется измеряемой величиной, принятым методом измерения и требуемой точностью результата измерения. Одну и ту же метрологическую задачу можно решить с помощью различных измерительных средств, которые имеют не только разную стоимость, но и различные точность и другие метрологические показатели, а следовательно, дают неодинаковые результаты измерения. Измерения с применением средств измерений недостаточной точности малоценны, даже вредны, так как могут быть причиной неправильных выводов. Применение излишне точных средств измерений экономически не выгодно. При выборе средств и метода измерений также учитывают диапазон измерений измеряемой величины, условия измерений, эксплуатационные качества средств измерений, их стоимость. Стремятся выполнить условие
где Величина предельной погрешности средства измерения - для грубых допусков - для остальных допусков где Допускаемая погрешность измерения включает случайные и неучтенные систематические погрешности измерения. Предельная погрешность средства измерения должна быть меньше допускаемой погрешности измерений, т.е.
ЛЕКЦИЯ№16
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

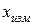 и истинным
и истинным 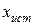 значениями измеряемой величины
значениями измеряемой величины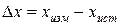 , (5)
, (5)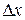 - погрешность измерения.
- погрешность измерения.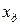 , и погрешность рассчитывается по формуле
, и погрешность рассчитывается по формуле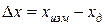 . (6)
. (6)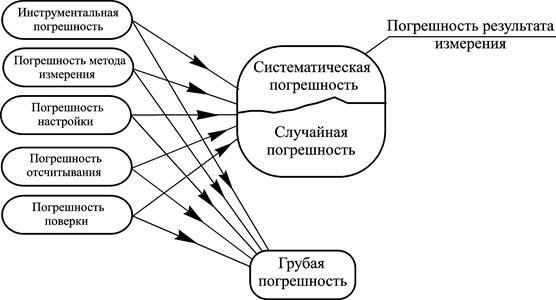
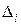 зависит от точности наблюдений и может быть определено по их среднему квадратическому отклонению, которое вычисляется по формуле
зависит от точности наблюдений и может быть определено по их среднему квадратическому отклонению, которое вычисляется по формуле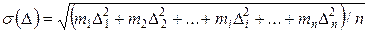 ,
, - число наблюдений, содержащих погрешность
- число наблюдений, содержащих погрешность 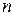 - общее число наблюдений.
- общее число наблюдений. . Вероятность появления погрешностей в каком-либо интервале значений определяется по плотности распределения вероятности случайных погрешностей
. Вероятность появления погрешностей в каком-либо интервале значений определяется по плотности распределения вероятности случайных погрешностей 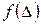 , которую вычисляют по формуле
, которую вычисляют по формуле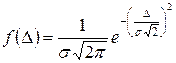 .
.
 при заданном значении
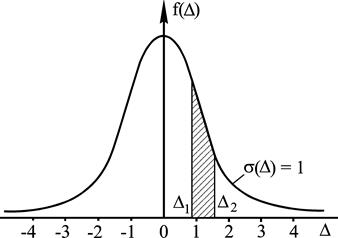
при заданном значении 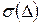 (рис. 59). Вероятность погрешностей в выбранном интервале значений, например
(рис. 59). Вероятность погрешностей в выбранном интервале значений, например 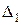 и
и 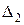 , равна отношению площади под кривой в этом интервале (показано штриховкой) ко всей площади под кривой. Кривая распределения стремится к нулю при увеличении абсолютных значений погрешностей. Вероятность появления погрешностей
, равна отношению площади под кривой в этом интервале (показано штриховкой) ко всей площади под кривой. Кривая распределения стремится к нулю при увеличении абсолютных значений погрешностей. Вероятность появления погрешностей 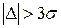 равна
равна  0,3 %, т.е. практически исключена. Погрешность
0,3 %, т.е. практически исключена. Погрешность  называется предельной погрешностью измерений. Погрешности измерений
называется предельной погрешностью измерений. Погрешности измерений 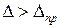 относятся к грубым погрешностям.
относятся к грубым погрешностям.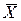 , подсчитанное по результатам
, подсчитанное по результатам 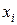 этих наблюдений и принимаемое за результат измерения:
этих наблюдений и принимаемое за результат измерения: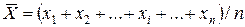 .
. ;
; .
.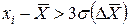 , то их исключают и выполняют повторные расчеты.
, то их исключают и выполняют повторные расчеты. ,
,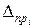 - предельные погрешности измерительных приборов, установочных мер, температурных деформаций, деформаций от измерительного усилия, базирования приборов и других факторов, из которых складывается суммарная погрешность данного измерения.
- предельные погрешности измерительных приборов, установочных мер, температурных деформаций, деформаций от измерительного усилия, базирования приборов и других факторов, из которых складывается суммарная погрешность данного измерения.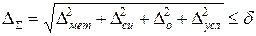 ,
,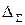 - суммарная погрешность измерения,
- суммарная погрешность измерения, 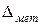 - предельная погрешность метода измерения,
- предельная погрешность метода измерения, 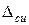 - предельная погрешность средства измерения,
- предельная погрешность средства измерения, 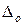 - погрешность оператора,
- погрешность оператора, 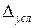 - дополнительная погрешность условий измерения,
- дополнительная погрешность условий измерения, 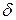 - допускаемая погрешность измерения.
- допускаемая погрешность измерения.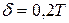 ;
;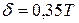 ,
,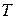 - допуск контролируемого параметра, задаваемый конструктором.
- допуск контролируемого параметра, задаваемый конструктором.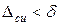 , однако экономически нецелесообразно выбирать
, однако экономически нецелесообразно выбирать 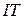 . Следовательно, точность средства измерения должна быть на порядок выше точности контролируемого параметра.
. Следовательно, точность средства измерения должна быть на порядок выше точности контролируемого параметра.


