
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямые однократные измерения с точным оцениванием
Погрешности
При однократных измерениях для получения результата измерения используют одно-единственное значение отсчета показаний прибора. Будучи по сути дела случайным, однократный отсчет При измерении с точным оцениванием погрешности проблема заключается в выявлении и оценке систематических и случайных составляющих погрешностей с последующим их раздельным суммированием. Особенностью однократного измерения является то, что законы распределения случайных составляющих неизвестны и представление о них приходится формировать на основе ограниченной априорной информации, а иногда и волевым порядком. Сравнительно легко, путем поверки или по паспортным данным может быть получена оценка систематической погрешности прибора, а анализом метода измерения – оценка систематической погрешности методического происхождения. При наличии в документации на прибор сведений о дополнительных систематических погрешностях, обусловленных влияющими величинами, эти погрешности также оцениваются и учитываются. После исключения из отсчета всех известных систематических погрешностей можно полагать, что погрешность исправленного результата В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допустимых основных и дополнительных погрешностей средств измерений применявшихся при поверке в качестве образцовых, погрешности расчетных поправок и др. Если неисключенные систематические погрешности оценены своими границами
Составляющие случайных погрешностей могут быть заданы средними квадратическими отклонениями
где Если же случайные составляющие погрешности заданы доверительными границами
Получив по отдельности оценки неисключенной систематической и случайной погрешностей результата однократного измерения, целесообразно сопоставить их между собой. В случае, когда оказывается необходимым учитывать обе составляющие, суммирование их выполняется по формуле (8). Как и при измерениях с многократными наблюдениями однократный отсчет может содержать грубую погрешность. Во избежание грубой погрешности однократное измерение рекомендуется повторить 2-3 раза, приняв за результат среднее арифметическое. Статистической обработке эти отсчеты не подвергаются. Результат однократного измерения записывается в форме ЛЕКЦИЯ№17
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.106.232 (0.005 с.) |
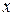 включает в себя инструментальную, методическую и личную составляющие погрешности измерения, в каждой из которых могут быть выделены систематические и случайные составляющие.
включает в себя инструментальную, методическую и личную составляющие погрешности измерения, в каждой из которых могут быть выделены систематические и случайные составляющие.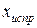 состоит из неисключенных остатков систематических погрешностей и случайных составляющих погрешностей. Неисключенные систематические погрешности переводят в категорию случайных и оценивают каждую составляющую своими границами. При этом рекомендуется распределение вероятностей принимать равномерным, если погрешности заданы границами и нормальным, если заданы средним квадратическим отклонением.
состоит из неисключенных остатков систематических погрешностей и случайных составляющих погрешностей. Неисключенные систематические погрешности переводят в категорию случайных и оценивают каждую составляющую своими границами. При этом рекомендуется распределение вероятностей принимать равномерным, если погрешности заданы границами и нормальным, если заданы средним квадратическим отклонением.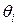 , доверительные границы суммарной неисключенной систематической погрешности определяют по формуле (7).
, доверительные границы суммарной неисключенной систематической погрешности определяют по формуле (7).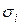 , найденными предварительно опытным путем по результатам многократных наблюдений, либо доверительными границами
, найденными предварительно опытным путем по результатам многократных наблюдений, либо доверительными границами 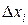 . В первом случае доверительные границы
. В первом случае доверительные границы 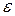 результирующей случайной погрешности результата определяются по формуле
результирующей случайной погрешности результата определяются по формуле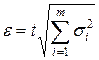 ,
,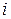 - ой составляющей,
- ой составляющей, 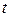 - коэффициент, зависящий от доверительной вероятности и числа наблюдений. В качестве
- коэффициент, зависящий от доверительной вероятности и числа наблюдений. В качестве 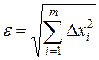 .
.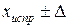 .
.


